1. Transfer Function
시스템에 대해 입력(Input)과 출력(Output) 사이의 관계를 나타내주는 함수를 전달함수(G(s))라 합니다.
전달함수(Transfer Function ; G(s))는 입력의 라플라스 변환에 대한 출력의 라플라스 변환의 비율로 정의됩니다.
간단히 Output / Input 이라 취급하면 됩니다.

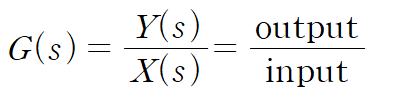
예시를 들어봅시다.
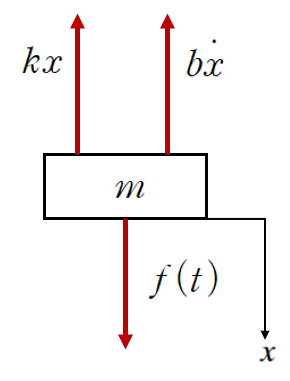
정지상태인 시스템에 f(t)라는 input force가 가해진 상황입니다.

위 시스템의 운동방정식을 세우면 다음과 같습니다.
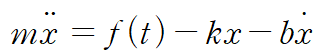
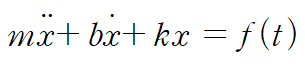
양변에 라플라스 변환을 취합니다. (도함수 공식 사용, 초깃값 0)

위 식으로부터 전달함수를 구할 수 있습니다.
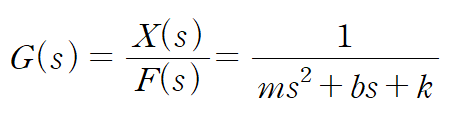
2. Method / Example
여러 개의 질량과 여러 개의 요소들로 구성된 경우 운동방정식을 세우기 힘듭니다.
몇 가지 규칙을 가지고 접근하면 쉽게 운동방정식을 세울 수 있습니다.
1. 가장 바깥쪽에 있는 변수부터
2. 상대변위 개념(바깥쪽 - 안쪽)
3. 작용 - 반작용(연결된 물체에 작용하는 힘은 반대방향)
(예제 1) 운동방정식을 구하고 전달함수 G(s) = Y(s)/U(s) 를 구하여라
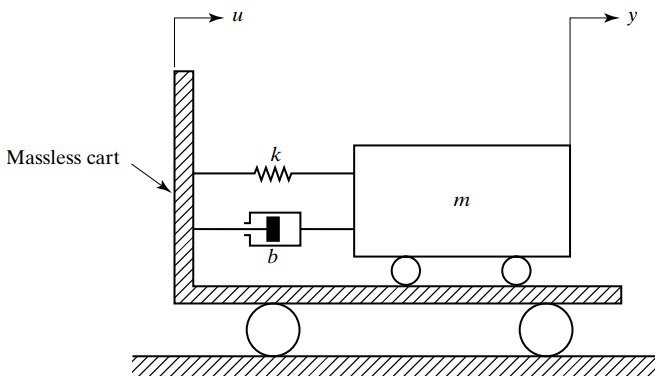
위와 같이 u,y 두 개의 명확한 인풋, 아웃풋이 있을 때는 하나의 운동방정식이 유도됩니다.
1. 가장 바깥쪽부터 : 가장 바깥쪽에 있는 y부터 해석합니다.
2. 상대변위 개념 : 스프링, 댐퍼 요소는 운동방향의 반대로 작용합니다.이때 u또한 스프링, 댐퍼 요소에 연결되어 있기 때문에 영향을 줍니다. 이것을 단순히 상대변위와 같은 관점에서 바라본다면 스프링이 늘어난 변위를 y-u로 생각할 수 있습니다.
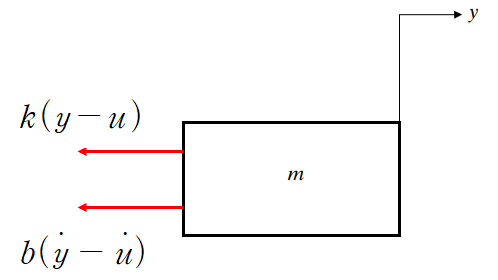
위와 같이 작용하는 힘을 모두 그렸다면 뉴턴 제 2 법칙 F = ma로부터 운동방정식을 구합니다.
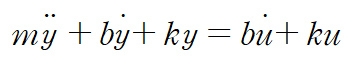
양변에 라플라스 변환을 취하고(별다른 언급이 없으면 초깃값은 0으로 생각합니다)
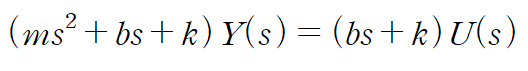
전달함수를 구합니다.

(예제 2) 운동방정식을 구하고 전달함수 G(s) = X(s)/P(s) 를 구하여라
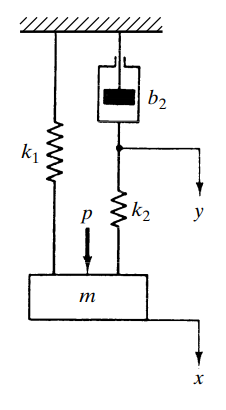
세 개의 변수가 등장했습니다. 이럴 경우 통상 두 개의 운동방정식이 만들어지는데 두 식을 연립해서 하나의 식으로 표현하는 과정이 추가됩니다.
1. 가장 바깥쪽부터 : 가장 바깥쪽에 있는 x부터 해석합니다.
2. 상대변위 개념 : 마찬가지로 스프링요소 k2에 작용하는 힘을 k2(x-y)라 세웁니다.
3. 작용 - 반작용 : 노드 y에 작용하는 힘은 스프링요소 k2와 댐퍼요소 b2에 의한 것입니다. 앞서 스프링요소 k2에 의한 힘의 크기가 k2(x-y)라 세웠으니 작용 - 반작용 법칙에 따라 y에 작용하는 힘은 반대방향으로 표시해줍니다.
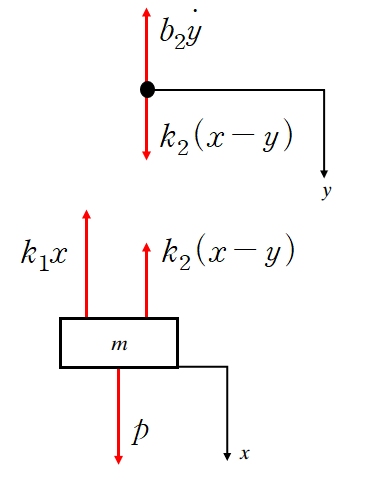
댐퍼의 경우 연결된 좌표계(변수)가 y밖에 없기 떄문에 댐퍼요소에 의한 힘은 b2 y' 가 됩니다.
이를 정리하면 두 개의 운동방정식을 얻습니다.
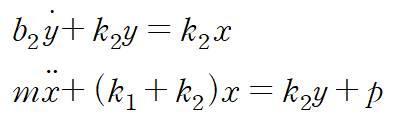
이때 노드 y에는 질량이 없기때문에 y'' 항이 없습니다.
두 식에 라플라스 변환을 취합니다.

우리는 X와 P의 관계만을 알고 싶으니 (1) 식을 정리해 Y를 소거시켜 줍니다.

이것을 (2) 식에 대입합니다.

양변에 b2s + k2 를 곱해 정리합니다.

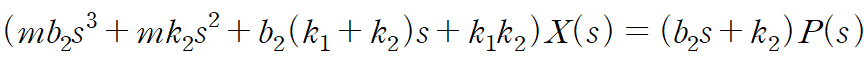
따라서 전달함수는 다음과 같습니다.
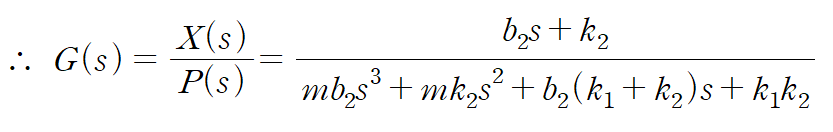
'기계공학 > 4대 역학' 카테고리의 다른 글
| [재료역학] 전단력 선도, 굽힘모멘트 선도 예제 (SFD, BMD) (0) | 2022.12.26 |
|---|---|
| [동역학] 상태공간 모델(State-space model), 전달함수(Transfer Function) (0) | 2022.12.15 |
| [동역학] 라플라스 변환의 초깃값 정리(Initial-value theorem) (0) | 2022.10.24 |
| [동역학] 라플라스 변환의 좌극한 (lower limit of the Laplace integral), 최종값 정리 (final-value theorem) (0) | 2022.10.23 |
| [동역학] Step, Ramp, Sinusoidal, Pulse, Impulse Function (0) | 2022.10.21 |