지난 시간에 이어 보의 순수 굽힘을 알아보도록 합시다. 크게 다섯 가지 공식이 등장합니다.

이번 글에서는 간단하게 다섯 가지 공식의 의미와 각 공식들의 표현을 배워봅시다.
공식 소개
(1) 변형률
중립면을 기준으로 높이 y에서의 보의 길이에 대한 축 방향(x축 방향) 변형률은 다음과 같습니다.
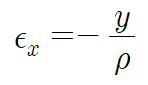
마이너스 부호가 붙는 이유는 ρ>0, y>0 일 때 압축, y<0 일 때 인장이 일어나기 때문입니다.
ρ<0 인 경우는 보가 아래쪽으로 쳐진(휘어진) 상태에서의 곡률반경입니다. U자로 휘면 ρ>0, 반대의 경우 ρ<0를 대입해야 합니다.
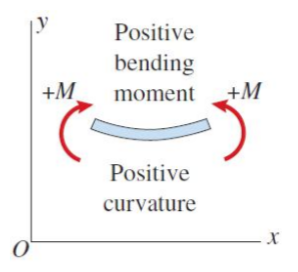
아래 그림처럼 보에 양의 굽힘 모멘트가 발생했다고 합시다.

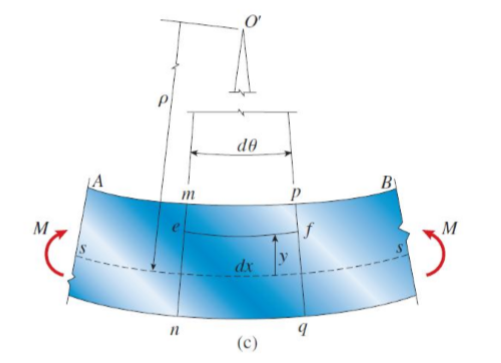
중립면으로부터 위에 위치한 ef 면은 길이가 줄어든 반면, 중립면 아래에 위치한 nq 면은 길이가 늘어나는 것을 볼 수 있습니다.
중립면으로부터 y만큼 떨어진 면 ef대한 변형률을 구해봅시다.
변형률의 정의는 길이변화량/길이 입니다.
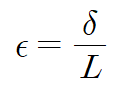
면 ef의 처음 길이는 dx입니다.
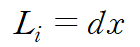
굽힘모멘트로 인한 변형이 일어난 후 면 ef의 길이는 반지름이 ρ-y 이고 중심각이 dθ 인 호의 길이와 같습니다.
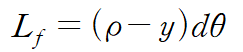
이때 중립면의 길이는 변하지 않으니 다음 관계식이 성립합니다.
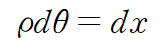
면 ef의 나중길이는 다음과 같이 정리됩니다.
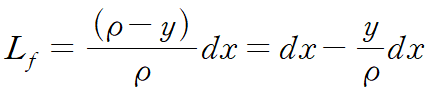
변위는 나중길이에서 처음길이를 뺀 것으로 다음과 같습니다.

x축 방향에 대한 변형률 εx는 다음과
같습니다.
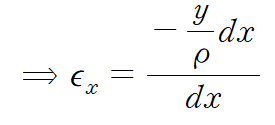
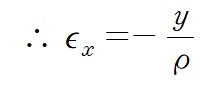
변형률의 크기는 y=c에서 최대입니다. 아래 식에서 좌변의 아래첨자 m는 maximum의 약자입니다.
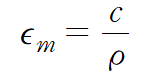
(2) 응력 분포
중립면을 기준으로 높이 y에서의 보의 응력 분포는 다음과 같습니다.
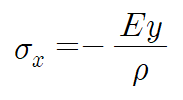
위 식은 훅의 법칙을 이용한 것으로, 보가 탄성 재료일 경우에 중립면을 기준으로 응력분포가 y축을 따라 선형적으로 증가함을 의미합니다.
이 응력은 단면에 수직인 방향으로 작용하지만, 굽힘에 대한 응력이기 때문에 굽힘응력(Bending stress 또는 Flexural stress)이라고 부릅니다.
재료가 선형탄성일 때 x축방향 응력과 x축방향 변형률의 관계는 다음과 같습니다.(훅의 법칙)

E는 재료의 탄성계수(Modulus of Elasticity)입니다.
위 식에 x축방향 변형률을 대입하면
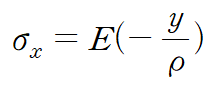
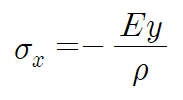
곡률 κ로 표현하면

이때 y=0인 지점인 중립면을 기준으로 응력의 부포가 바뀌게 됩니다.
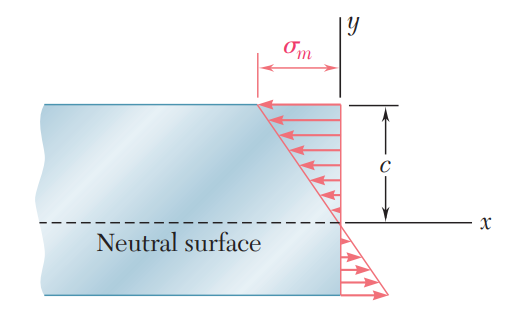
위 그림은 곡률이 positive curvature, 즉 양의 곡률일 때 응력분포를 나타낸 것으로 중립면 기준 상부는 압축, 하부는 인장임을 의미합니다.
c는 중립축으로부터 가장 먼 지점까지의 길이 입니다.
최대 굽힘응력의 크기는 y=c일 때 응력의 크기입니다.
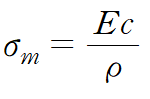

(3) 중립축의 위치
중립축(중립면)은 다음과 같은 식을 통해 유도됩니다.
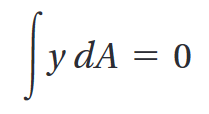
위 식은 z축에 대한 단면의 면적 모멘트가 0임을 의미하며, 단면의 도심이 곧 중립축의 위치임을 의미합니다.
보에 수직력이나 굽힘모멘트만이 작용하기 때문에 x축 방향 합력은 0입니다.

미소구간 dx에 작용하는 미소힘 dFx 는 다음과 같습니다.
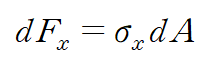
이를 적분한 합력은 다음과 같습니다.
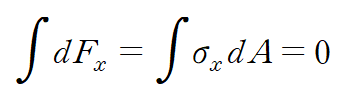
굽힘응력을 대입하면
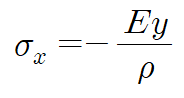
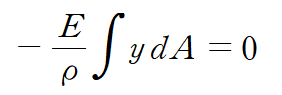
따라서 아래 단면 1차모멘트가 0입니다.

그러기 위해서는 y축이 단면의 도심(Centroid) 이어야만 합니다.
(4) 모멘트-곡률 관계식
보에 대해 발생하는 굽힘모멘트 M과 곡률 κ 의 관계식은 다음과 같습니다.
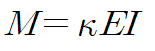
곡률 대신 곡률 반경 ρ으로 관계식을 표현하면 다음과 같습니다.
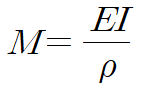
간단히, 가해지는 굽힘모멘트 M에 대해 곡률 κ가 굽힘 강도 EI를 통해 정해지거나, 굽어진 정도에 따라 굽힘모멘트 M을 구할 수 있다는 것을 의미합니다.
Z축을 기준으로 하는 모멘트는 다음과 같습니다.
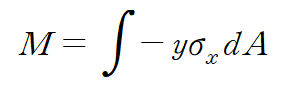
마이너스(-)부포가 붙는 이유는 굽힘모멘트의 부호 때문입니다.
위 식에 마찬가지로 굽힘응력을 대입하면
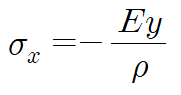
다음과 같이 정리됩니다.
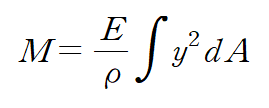
우변의 적분이 단면 2차 모멘트이기 때문에
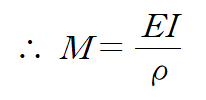
단순히 굽힘응력을 대입하는 과정에서 굽힘모멘트의 부호를 양으로 맞추기 위해 처음 식에서 마이너스(-)부호를 곱해주었다고 생각해도 지장 없습니다.
(5) 굽힘 공식
중립면을 기준으로 높이 y에서의 x축 방향 굽힘 응력은 다음과 같습니다.
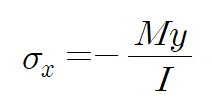
가해진 굽힘모멘트와 관성모멘트 I에 대해 굽힘 응력이 정의된다는 것은 외부에서 가해지는 굽힘모멘트 뿐만 아니라 보의 단면 또한 응력과 깊은 관계가 있음을 의미합니다. "기하학적 형상"이라고 하지요.
굽힘응력과 변형률 관계식을 조금 변형하면 아래와 같습니다.

이 식을 모멘트-곡률 관계식에 대입합니다.
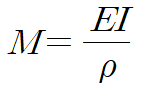
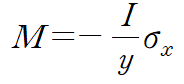
굽힘응력에 대해 정리하면 굽힘 공식을 얻을 수 있습니다.
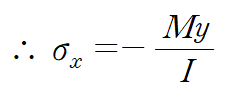
마찬가지로 최대 굽힘응력은 y=c인 지점에서 발생합니다.
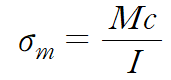
굽힘 공식은 가해진 굽힘모멘트 M에 대해 굽힘응력을 구하기 유용합니다.
여기까지 순수 굽힘 - 공식편 이었습니다. 다음 시간에는 예제를 풀어보며 실제로 공식들이 어떻게 사용되는지, 어떻게 사용해야 하는지 감을 익혀봅시다.
'기계공학 > 4대 역학' 카테고리의 다른 글
| [재료과학] 보의 처짐 예제 (1) | 2023.02.24 |
|---|---|
| [재료역학] 보의 처짐 : 처짐 미분방정식 유도 (Deflections of Beams) (0) | 2023.01.01 |
| [재료역학] 보의 순수 굽힘 - 개념 편 (2) | 2022.12.26 |
| [재료역학] 전단력 선도, 굽힘모멘트 선도 예제 (SFD, BMD) (0) | 2022.12.26 |
| [동역학] 상태공간 모델(State-space model), 전달함수(Transfer Function) (0) | 2022.12.15 |