#동역학
#시스템해석

https://search.shopping.naver.com/book/catalog/32464065666
System Dynamics : 네이버 도서
네이버 도서 상세정보를 제공합니다.
search.shopping.naver.com
1. State Equation & Output Equation
(1) State Equation
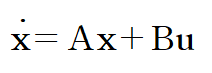
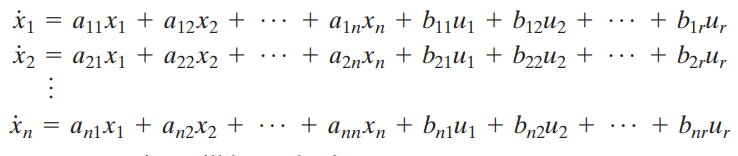
(2) Output Equation
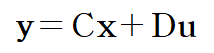
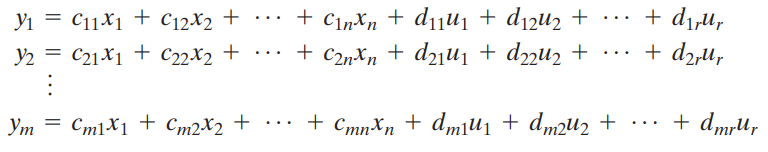
> 용어설명
x : State Vector
u : Input Vector
y : Output Vector
A : State Matrix (A matrix)
B : Input Matrix (B matrix)
C : Output matrix (C matrix)
D : Direct Transmission matrix (D matrix)

State equation은 state variable(x1, x2, . . . , xn)의 개수만큼 유도해야 합니다 (State를 결정하기 위해서 ; 선형대수학의 Basis 개념과 유사)
동역학 시스템에서는 운동방정식과 state 선언에 의해 state equation을 유도할 수 있습니다.
state equation을 유도하는 방법은 다음과 같습니다.
- 운동방정식 세워서 계수 정리 (n계 미분방정식 -> n 개의 state variable)
- state variable 선언 (x1 = output)
- 앞선 state variable을 미분한 것을 새로운 state variable 로 선언
state - space 로 나타내기 위해서(행렬 표현) 두 가지 방법을 이어서 진행합니다.
4. 운동방정식에 state variable 대입 (x1)하여 state equation 정리
5. Output equation 정리
(예제 1) Obtain a state - space representation of the system
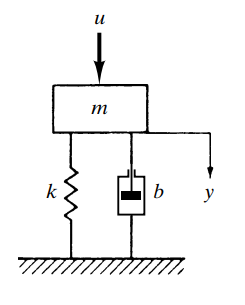
1. 운동방정식을 세웁니다.

이것을 고계도함수의 계수가 1이 되도록 정리합니다.
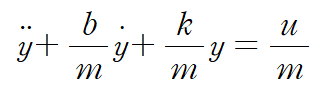
2. state variable 선언 (x1 = y)
x1 을 output 에 해당하는 y로 정의합니다.
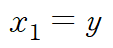
3. x1을 미분한 것을 두 번째 state variable로 정리합니다. (첫 번째 state equation)
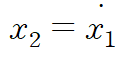
4. 운동방정식의 y 대신 x1를 대입하여 또다른 state equation을 얻습니다.
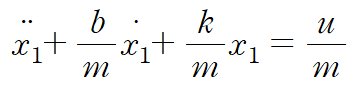
state equation의 좌변이 1계 도함수이므로 그에 맞추어 x1``대신 x2`을 대입합니다. (과정 3)
또한 우변에 미분항이 없어야 하므로 x1`에도 x2를 대입합니다.

이상을 정리하면 아래와 같이 두 번째 state equation을 얻습니다.
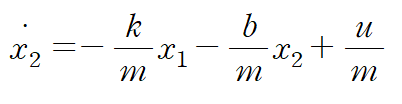
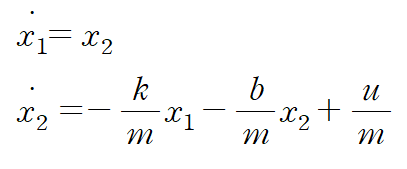
이것을 행렬형태로 표현하면 다음과 같습니다.
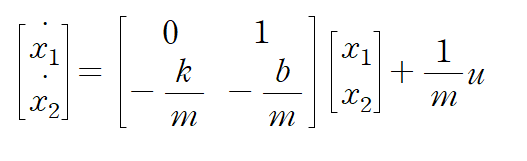
5. Output equation
x1을 선언할 때의 정의에 따라서 output equation을 간단히 정리할 수 있습니다.
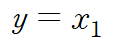
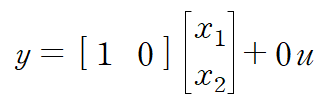
State - space modelling의 경우 여러 개의 연립미분방정식이 유도되더라도 하나로 통합할 필요 없이 각 방정식에서 state를 정의해도 된다는 장점이 있습니다. 또한 state는 unique하지 않기 때문에 어떻게 정의하느냐에 따라 천차만별입니다. 예제 1은 간단한 예시를 든 것이고 x1 = -y, x2 = x1` +x1 처럼 정의해도 상관 없습니다. 그때의 state equation을 구성하는 요소들은 조금 달라지겠지요
2. with Input Derivatives
하지만 input에 도함수 형태가 있을 경우 굉장히 복잡해집니다. state equation에서 input의 미분항은 없기 때문에 state 선언에 적절한 수정이 필요합니다.
(1) method 1
Input function(u)를 포함한 운동방정식을 아래와 같이 세웁니다.
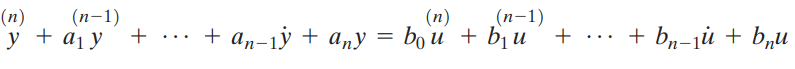
여기서 주의할 점은 좌변에서 output 최고계도함수의 계수가 1이라는 것과 우변 input function들은 좌변의 output 최고계도함수의 미분차수를 따라서 설정해야 한다는 것입니다.( 좌변에는 y''이 있고 우변에는 u'만 존재한다면 0u'' 처럼 써줘야 함)
1. method 1에서는 전형적인 state equation을 가집니다.
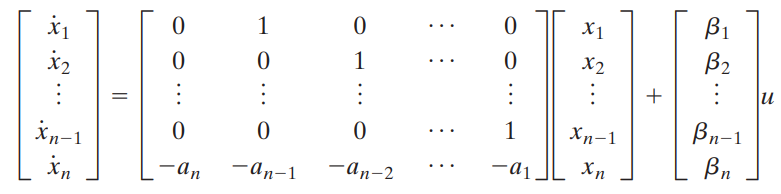
A matrix(state matrix)가 굉장히 복잡해보이지만 사실 앞선 예제1과 같이 x1을 설정하고 x2를 x1`으로 정의한 방법과 같습니다. 앞선 state variable을 미분한 것을 새로운 state로 정의합니다. 마지막 줄은 운동방정식을 정리해서 얻습니다.
2. B matrix
문제는 B matrix(input matrix)입니다. 아래 규칙을 사용하여 정리합니다. a는 output의 계수, b는 input의 계수입니다.
우변에서 첫 항은 bn으로 고정되고 a는 1부터 n까지 올리고 b는 β0까지 내린다고 생각하면 쉽습니다.
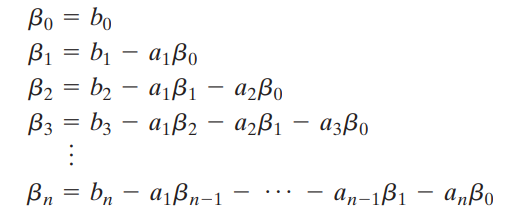
β의 유도는 생략하겠습니다.
3. Output equation
마찬가지로 y = x1 + β0 u 의 전형적인 형태를 가진다고 생각할 수 있습니다.
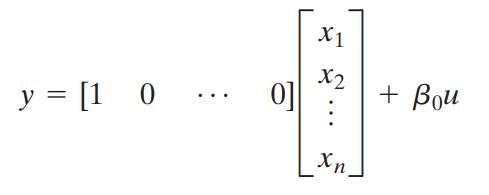
(예제 2) Obtain a state - space representation of the system (method I)
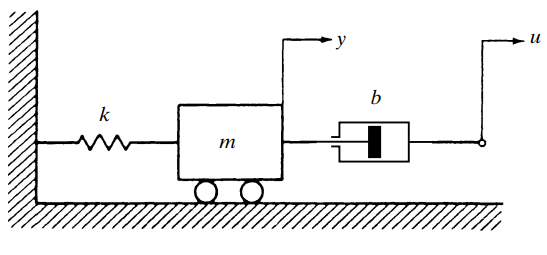
시스템의 운동방정식을 유도합니다.
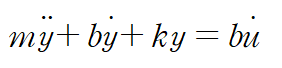
양변을 m으로 나누어 y``의 계수를 1로 맞추고 우변을 정리합니다.
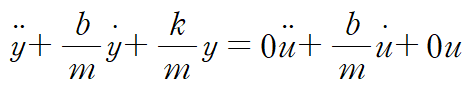
계수를 정리하고 β를 구합니다.
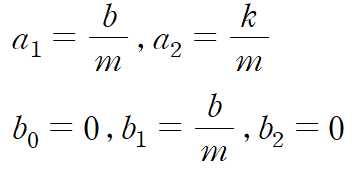
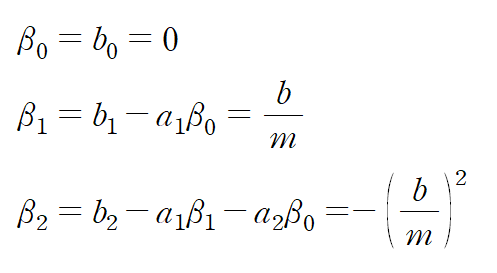
A matrix는 우변이 0이라고 생각하고 두고 예제 1과 같이 정리하고 (input과 무관)
B matrix는 β1, β2 로 구성합니다. ( β0가 아님에 주의!)

마지막으로 Output equation을 정리합니다.
y = x1 + β0u 입니다.
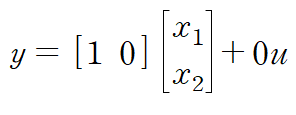
(2) method 2
method 2는 매개변수 z와 매개함수 Z(s)를 사용하는 방법입니다.
Y(s)/U(s) 꼴 전달함수를 아래와 같이 Z(s)라는 어떤 함수를 통해 표현하는 것부터 시작합니다.
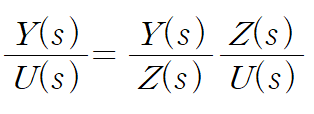
예시 2의 시스템을 그대로 가져오겠습니다.
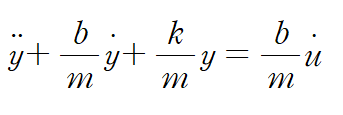
이것의 전달함수를 구하면 아래와 같습니다.
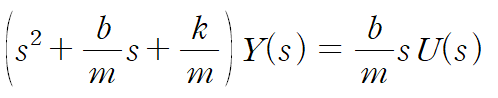
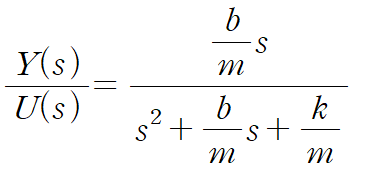
이것을 Z(s)를 사용해 표현합니다.
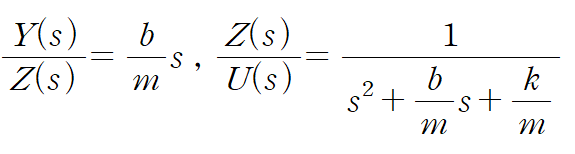
각 식에 라플라스 역변환을 취합니다.
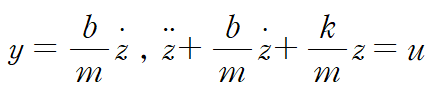
매개로 삼은 z를 state variable로 정의합니다.
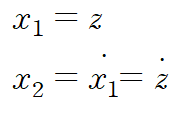
이것을 역변환을 취한 식에 대입합니다.
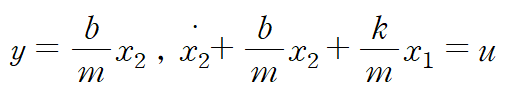
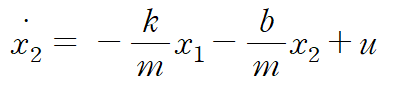
위 식을 정리하면 state equation과 output equation 을 얻습니다.
y가 포함된 식에서 output equation을 얻을 수 있음을 직관적으로 알 수 있습니다.
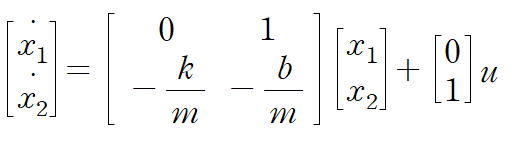
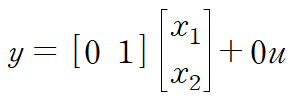
3. Transfer Function
앞서 정리한 state equation과 output equation으로부터 전달함수 G(s)를 유도할 수 있습니다.
전달함수는 Output/Input이므로 Y(s)와 U(s) 로 이루어진 식이 필요합니다.
두 식에 라플라스 변환을 취하고 X(s)를 소거하면 전달함수가 유도됩니다.
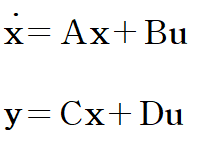
시간과 관련있는 "x,u,y" 벡터들에 라플라스 변환을 취합니다.
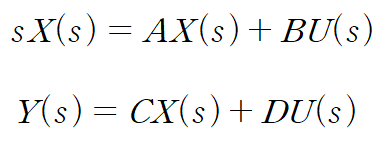
첫 번째 식에서 우변의 첫 번째 항을 이항하고
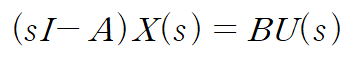
양변에 X(s) 앞에 있는 (sI-A)의 역행렬을 양변에 곱합니다.
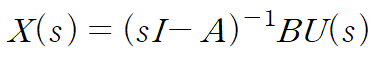
이것을 두 번째 식에 대입하여 정리합니다.
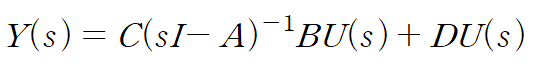
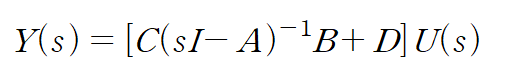
전달함수는 다음과 같습니다.
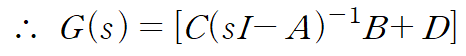
'기계공학 > 4대 역학' 카테고리의 다른 글
| [재료역학] 보의 순수 굽힘 - 개념 편 (2) | 2022.12.26 |
|---|---|
| [재료역학] 전단력 선도, 굽힘모멘트 선도 예제 (SFD, BMD) (0) | 2022.12.26 |
| [동역학] 전달함수(Transfer Function) 정의, 연립 운동방정식 예제 (0) | 2022.10.26 |
| [동역학] 라플라스 변환의 초깃값 정리(Initial-value theorem) (0) | 2022.10.24 |
| [동역학] 라플라스 변환의 좌극한 (lower limit of the Laplace integral), 최종값 정리 (final-value theorem) (0) | 2022.10.23 |