
테일러 급수전개
테일러 급수전개는 미분방정식을 공부하면서도 나오는 내용이고, 어떤 값을 근사하는 데도 사용되는 유용한 Tool이다. 계산기에는 이 테일러 급수전개 꼴로 수식이 들어가있어, 우리가 원하는 값을 근사적으로 계산해준다고 한다. 예를 들어

의 값을 계산기에게 물어보면 계산기는 다음과 같은 계산을 실행한다.

(i) 테일러 급수 전개
Basic Concept는 "미분 가능한 함수를 급수의 형태로 나타내보자"이다. 갑자기 왜 급수의 형태로 나타내는거냐고 묻지말고 그냥 그렇게 해보고 싶었나보다 하고 넘어가라. 위대한 발견은 종종 우연이라는 발상에서 시작되니까.
미지의 상수

을 이용해 멱급수 꼴로 f(x)를 전개하면(가정하면) 아래와 같다


x=a에서의 멱급수 전개를 살펴보자. 궁극적으로

을 구하는 게 우리의 목표임을 기억하고
x=a에서의 멱급수 전개식의 양변에 x=a를 대입하는 것부터 출발한다. x=a를 대입하면 우변은

만 남는다.
그 다음 양변을 미분해서 x=a를 대입하니

만 남았다. 이 과정은 반복한다

짜잔

은 이렇게 정리된다. 이

을 이용해서 x=a에서의 멱급수 전개를 다시 정리하면

이런 형태의 아름다운 멱급수를 얻을 수 있다. 이를 테일러 급수라고 한다
추가로, x=0에서의 멱급수전개를 Maclaurin 급수라고 한다

(ii) 대표적인 테일러 급수
e^x, cos x, sin x와 같은 대표적인 함수들을 x=0에서 전개한 테일러 급수는 다음과 같다
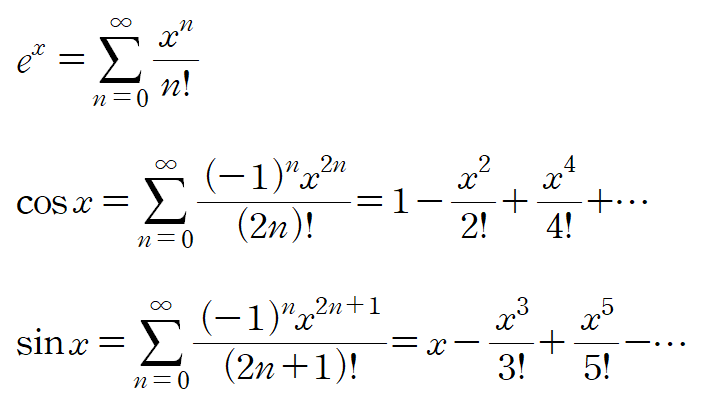
(iii) 급수전개 시각화
초월함수들이 어떻게 다항함수의 합으로 표현될 수 있는가?에 대한 물음은 위에서 증명했다. 무한 번 미분가능한 함수라면 가능하다는 것이 수식으로는 증명이되었지만, 정말로 그럴까? 라는 물음에 대한 답변으로서 실제 그래프를 통해 테일러 급수전개를 시각해보았다. 대표함수 세 가지에 대해 각각 두 지점에서 급수전개하였으며 사용자가 임의로 k값을 조정하면서 근사되는 과정을 볼 수 있다

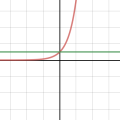
테일러 급수전개 (1)
www.desmos.com

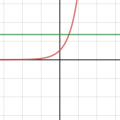
테일러 급수전개 (2)
www.desmos.com

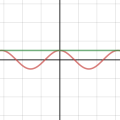
테일러 급수전개 (3)
www.desmos.com

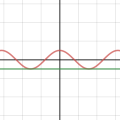
테일러 급수전개 (4)
www.desmos.com

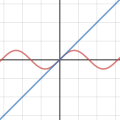
테일러 급수전개 (5)
www.desmos.com

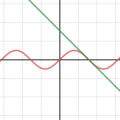
테일러 급수전개 (6)
www.desmos.com
'MATHEMATICS > 미분적분학' 카테고리의 다른 글
| [미분적분학] 야코비안(Jacobian) 예제 (0) | 2021.02.06 |
|---|---|
| [미분적분학] 이상적분 (Improper Integral) (1) | 2021.01.17 |
| [미분적분학] 삼각치환법 (Trigonometric Subtitution) (0) | 2021.01.17 |
| [미분적분학] 교대급수 판정법 (0) | 2020.12.06 |
| [미분적분학] 벡터함수의 미분 (0) | 2020.10.09 |