중적분은(double integral)은 기본적으로 주어진 영역 R에서 수행되는 계산이다. 이 영역 R의 x범위, y범위를 구하고 dxdy 또는 dydx 로 미분소 dA를 치환해 계산한다.
그러나 가끔 x와 y의 범위로 깔끔하게 나타내기 어려운 경우가 있다. 원이나 이차곡선 영역이 대표적인 예고, 아래와 같은 형태의 영역도 해당된다.
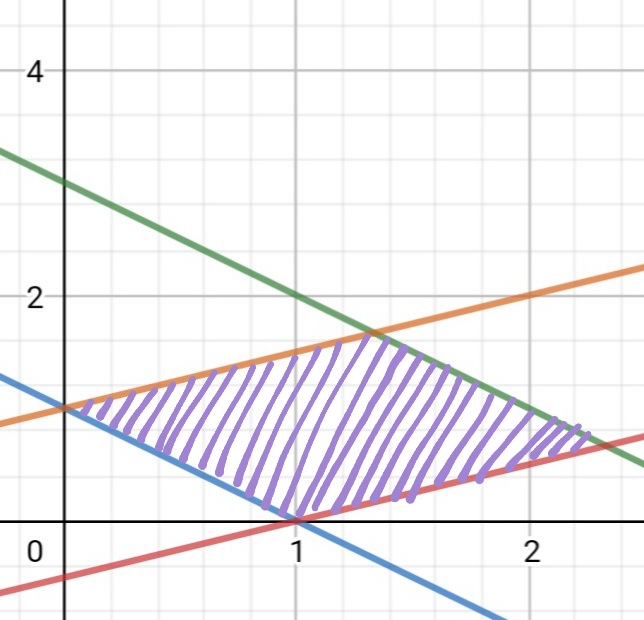
이럴 때면 일반 1차원 정적분의 치환적분과 비슷한 개념으로 변수를 바꿀 수 있는(chage of variables) 유용한 도구 "Jacobian"을 떠올리자. 한국어로는 야코비안으로도 번역되는데 이 Jacobian은 치환적분시 dx 가 dt로 바뀌는 과정 중 dt에 해당하는 느낌이다.
Jacobian의 정의와 이를 이용한 중적분 계산을 간단히 살펴보고 바로 예제풀이에 들어가자
x와 y가 두 변수 u, v로 이루어졌다면, 다시말해 x(u,v) , y(u,v) 라면 다음 행렬식을 Jacobian(야코비안)이라 정의한다
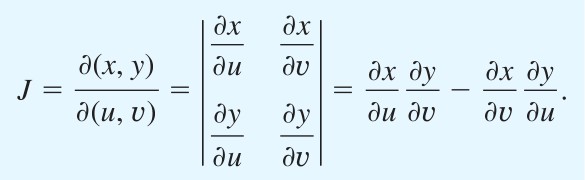
야코비안의 정의
x와 y가 u, v로 이루어졌다기보다는 x와 y를 u와 v로 표현했을때가 조금 더 적절하다. 실제로 x와 y가 u,v의 함수일 때보다 임의의 u와 v를 설정하는 식으로 사용하니까. 정의 다음에 나오는 예제에서 느낌 잡아볼 테니 어지러워도 걱정말자 ;)(찡긋)
야코비안을 이용해 이중적분을 표현할 경우, 일변수 함수의 치환적분처럼 세 가지가 바뀐다.
1. dxdy => dudv (적분하는 문자의 변환)
2. R => R* (적분을 수행하는 영역의 변환)
3. f(x,y) => f(u,v) (피적분함수의 변환)
+) 절댓값 야코비안 곱하기
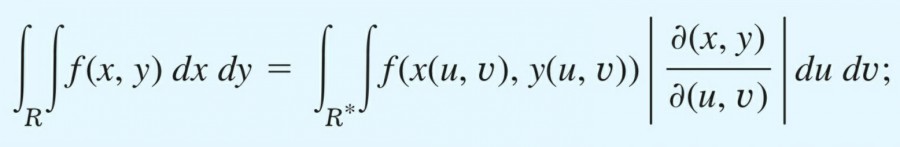
차근차근 1번부터 알아보자. 사실 설명할 게 없는 게 이 1번인게 우리가 원하는 건 적분을 수행하는 주체인 변수를 바꿔 좀 더 편리하게 계산하기 위함이다. 그러기 위해선 당연히 미분소 dxdy가 dudv로 바뀌어야 맞다.
(말이 이상할 수도 있는데 좀 어렵다면 요리를 하기 위해 생 채소를 사용하는 게 아니라 손질하여 사용하는 것을 떠올려보자. 생 채소가 dxdy, 손질된 새로운 채소가 dudv 그리고 잘려나간 껍질 부분을 보충해주기 위한 게 야코비안의 절댓값에 대응한다)
영역 R에서 R* 으로의 변환은 마치 치환적분에서 적분범위가 바뀌는 것과 같다
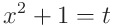
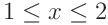
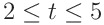
이렇게 일련의 과정을 거쳐 적분범위가 변하는 것처럼
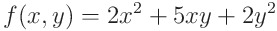
라는 피적분함수에 대해
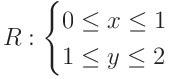
라는 영역에서 이중적분을 수행한다고 하자
이때 피적분함수가 아래와같은 간단한 꼴로 바뀌므로
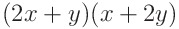
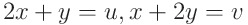
라고 새로운 변수 u와 v를 사용해 치환할 수 있다. 이때 새로운 이중적분을 수행하는, 다시 정의된 영역 R*은 아래와 같다.
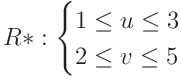
마지막 3번째. 피적분함수의 변환이다. 별 어려운 건 없고 하던대로 새로 정의한 변수들로 기존함수를 표현하는 것이다. 바로 이전 경우에서 살펴보면
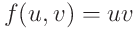
처럼 피적분함수의 변환이 일어난다
기본적인 야코비안의 개념은 여기까지. 예제를 통해 감을 잡아보자 라고 하기에는 아직 야코비안 계산을 하지 않았다(..??) 바로 이전 예시를 통해 야코비안 계산을 해보자
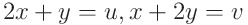
위처럼 u와 v를 정의했었다
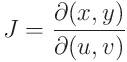
헌데 우리가 구해야 하는 야코비안은 x(u,v), y(u,v)에 대해 수행된다. 즉 x와 y 를 u,v로 다시 표현해줘야 한다
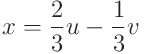
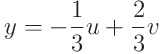
야코비안의 정의에 따라 계산을 해보자
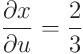
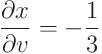
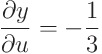
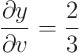
라는 일련의 계산을 거쳐
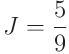
을 얻는다
이게 끝이다!
예제 풀이
(1) 다음 이중적분을 계산하여라
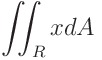
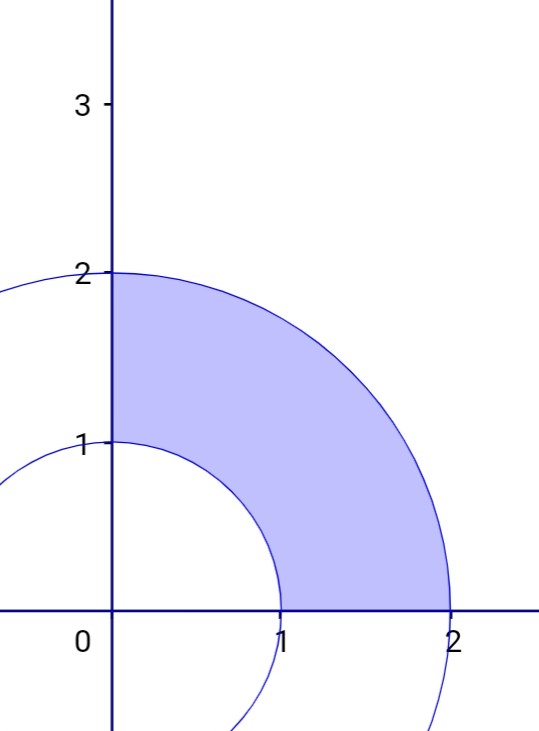
주어진 영역을 x와 y로 표현하는 건 무리가 있습니다. 물론 근호를 사용해 나타낼 수도 있지만 영역을 한 번에 정의하는 건 어렵습니다. 적어도 두 개로 쪼개야 합니다.
x와 y가 아닌 r과 θ를 이용한다면 훨씬 간단하게, 한 번에 영역을 정의할 수 있습니다.
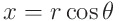
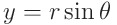
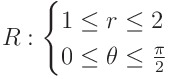
짠 간단해졌습니다. 이제 야코비안을 구해 중적분을 계산하면 끝입니다.
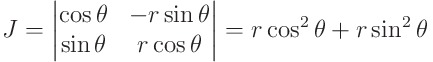
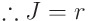
따라서 중적분은 아래와 같이 정의됩니다
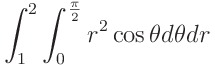
θ부터 적분해주면 0부터 π/2 까지 cos θ 의 정적분 값이 1 이므로
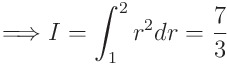
3분의 7이라는 답을 얻습니다
(2) 다음 이중적분을 계산하여라
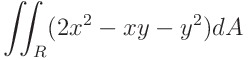
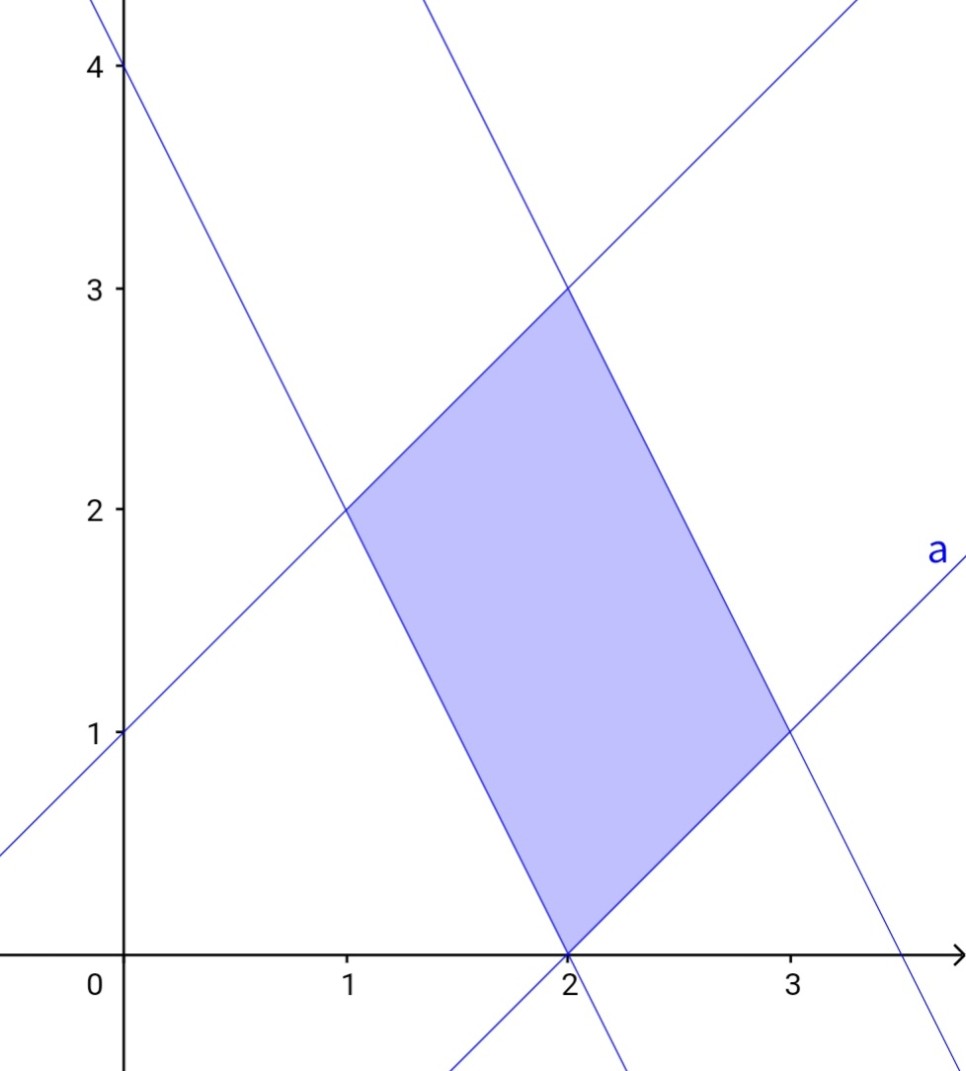
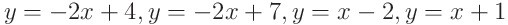
피적분함수를 보자마자 감이 오죠?
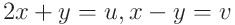
이렇게 설정해주면 영역도 한 번에 정의할 수 있습니다. 마치 직선이 움직인다는 느낌으로 받아들이시면 됩니다.
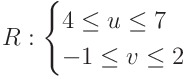
야코비안은 아래와 같습니다.
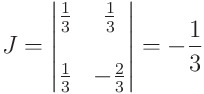
이를 이용해 중적분을 다시 정의하면 아래와 같습니다
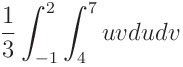
u에 대한 적분을 먼저 해줍시다
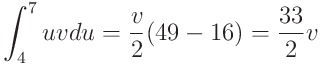
v도 계산하면 다음과 같습니다
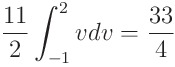
따라서 중적분의 값이 33/4 임을 알 수 있습니다
'MATHEMATICS > 미분적분학' 카테고리의 다른 글
| [미분적분학] 이상적분 (Improper Integral) (0) | 2021.02.06 |
|---|---|
| [미분적분학] 비판정법 (Ratio Test) (0) | 2021.02.06 |
| [미분적분학] 이상적분 (Improper Integral) (1) | 2021.01.17 |
| [미분적분학] 삼각치환법 (Trigonometric Subtitution) (0) | 2021.01.17 |
| [미분적분학] 테일러 급수전개 (0) | 2020.12.06 |