반응형
1. Lower limit of the laplace integral
라플라스 변환의 우극한과 좌극한을 다음과 같이 정의합니다.
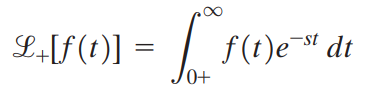
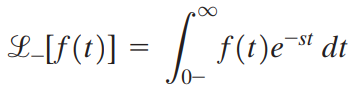
라플라스 변환의 좌극한은 우극한을 이용해 나타낼 수 있습니다.
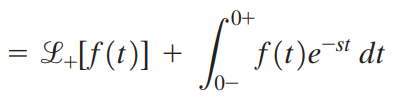
만약 f(t)가 impulse function을 포함하고 있다면 아래 정적분은 0이 아닙니다.
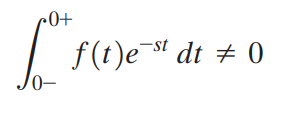
이것을 바꿔 말하면 f(t)가 t = 0에서 임펄스 함수를 가지고 있지 않다면 라플라스 변환의 좌극한과 우극한은 다음과 같습니다.
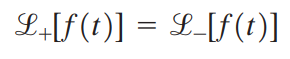
2. Final-value Theorem
최종값 정리는 f(t)의 steady state(정상 상태)와 관련이 있습니다. 초기에 시스템이 인풋을 받은 이후로 긴 시간이 흐르면 시스템은 일정한 움직임을 보입니다. 즉 f(t)의 양의 무한대 극한에 관한 이야기입니다.
최종값 정리는 다음과 같습니다.
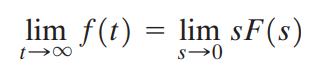
도함수 f'(t)의 라플라스 변환에 s->0 극한을 취함으로 간단히 증명할 수 있습니다.
도함수에 대한 라플라스 변환은 다음과 같습니다.
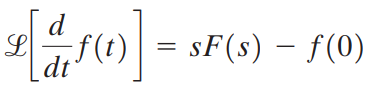
이것의 양변에 s->0 극한을 취합니다.
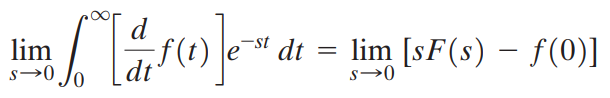
좌변에서 e^-st -> 1이므로 다음과 같습니다.
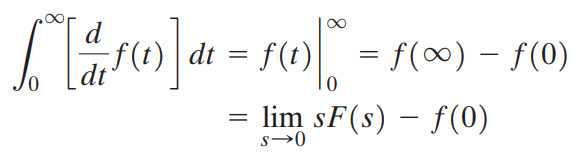
만약 t가 양의 무한대로 갈 때 f(t)의 극한이 존재한다면 아래 식이 성립합니다.
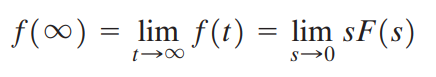
만약 s -> 0 sF(s) 의 극한이 존재하지 않는다면(발산) f(t)는 일정한 값으로 수렴하지 않는다고 이해할 수 있습니다.
반응형
'기계공학 > 4대 역학' 카테고리의 다른 글
| [동역학] 전달함수(Transfer Function) 정의, 연립 운동방정식 예제 (0) | 2022.10.26 |
|---|---|
| [동역학] 라플라스 변환의 초깃값 정리(Initial-value theorem) (0) | 2022.10.24 |
| [동역학] Step, Ramp, Sinusoidal, Pulse, Impulse Function (0) | 2022.10.21 |
| [유체역학] 가속도장 (Acceleration Field) 유도, 물질도함수 (0) | 2022.10.20 |
| [열역학] 검사체적에서 에너지 방정식 (3) : 과도유동(transient flow process) (0) | 2022.10.01 |