1. 가속도장 유도

유체는 많은 입자들의 집합체이기 때문에 하나의 입자를 관찰하는 것보다 전체입자에 대한 해석이 더 유용할 때가 많습니다. (특정 입자의 이동을 알아보는 문제의 경우는 반대) 때문에 Field 라는 도구를 이용해 각 점에서의 유체 운동을 편하게 기술할 수 있습니다.
3차원 상에서 전체 입자의 속도를 표현하면 다음과 같습니다.

x,y,z가 시간 t에 영향을 받는다고 생각하여 유도합니다.
가속도 a는 속도를 시간에 대해 미분한 것이므로 다음과 같습니다.

연쇄법칙(Chain Rule)을 적용하면 같이 네 개의 항으로 전개됩니다. (미분하는 변수인 t와 관계가 있는 다른 변수들을 거쳐간다는 느낌으로 이해하시면 쉽습니다)


이상의 미분결과를 통해 가속도를 정리한 것은 아래와 같습니다.
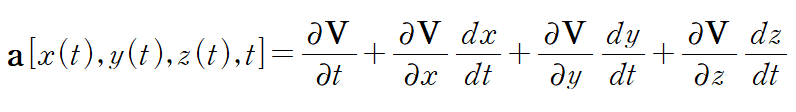
2. 가속도식의 간소화
먼저 속도 V의 x,y,z 방향 성분을 u,v,w 라 한다면 다음과 같이 가속도식을 간소화할 수 있습니다.


이것을 델 연산자(▽ ; "nabla") 를 사용해 벡터곱 형태로 표현할 수 있습니다.
델 연산자의 정의는 아래와 같습니다.
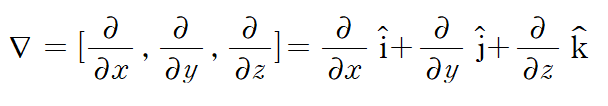

속도 V의 x,y,z방향 성분을 각각 u,v,w라 한다면 가속도식의 2,3,4 번째 항을 하나로 정리할 수가 있습니다.


이상의 결과로부터 가속도식은 다음과 같이 표현됩니다.

3. 물질도함수
위 마지막 식에서 물질도함수의 정의가 등장합니다.

물질도함수(material derivative)
물질도함수는 대문자 D를 사용해 표현합니다.
물질도함수라는 개념은 역학(특히 열, 유체)에서 가속도 뿐 아니라 다양한 방면에서 유용한 해석을 제공합니다.
물질도함수의 첫 번째 항은 시간에 대한 변화율(local derivative)을, 두 번째 항은 유체 유동에 의한 변화율(convective derivative)을 의미합니다.
4. 특정 상황에서의 가속도장
특정 조건 하에서 가속도항은 매우 간단해집니다.
(1) x방향 유동만 고려(1차원 유동)
속도의 x성분인 u만 남으니 두 개의 항만 남게 됩니다.

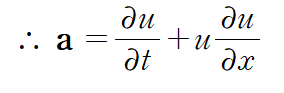
(2) 정상유동(시간에 의한 속도 변화 X)
속도가 시간이 흘러도 일정하다면 시간에 대한 속도 변화율은 0이 됩니다.

이를 정리하면 다음과 같습니다.

델 연산자로 표현하면 하나의 항으로 정리됩니다.

'기계공학 > 4대 역학' 카테고리의 다른 글
| [동역학] 라플라스 변환의 좌극한 (lower limit of the Laplace integral), 최종값 정리 (final-value theorem) (0) | 2022.10.23 |
|---|---|
| [동역학] Step, Ramp, Sinusoidal, Pulse, Impulse Function (0) | 2022.10.21 |
| [열역학] 검사체적에서 에너지 방정식 (3) : 과도유동(transient flow process) (0) | 2022.10.01 |
| [열역학] 검사체적에서 에너지 방정식 (2) : 정상상태 유동(steady state flow) (1) | 2022.09.30 |
| [열역학] 검사체적에서 에너지 방정식 (1) : 기본 식 설명 (0) | 2022.06.08 |