특정 함수에 대한 시스템의 방정식이 전형성을 보이기 때문에 간단히 정리한 여러 function들에 관한 내용입니다.
1. Step Function
Unit step function 은 함숫값이 1인 함수고 step function은 함숫값이 임의의 상수 A입니다. system dynamics에서는 대부분 초기상태 t = 0에 가해진 input이기 때문에 t = 0 에서 상수 input을 주는 함수라 생각하면 됩니다.

step function의 좌극한과 우극한은 다음과 같습니다.

step function의 라플라스 변환은 다음과 같습니다.

2. Ramp Function
다음과 같은 함수를 Ramp function이라 부릅니다.
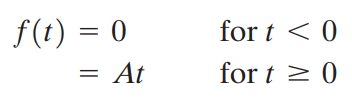
ramp function의 좌극한과 우극한은 다음과 같습니다.
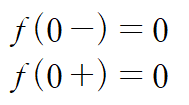
ramp function의 라플라스 변환은 다음과 같습니다.

3. Sinusoidal Function
"사인파"로 해석되는 Sinusoidal Function입니다.
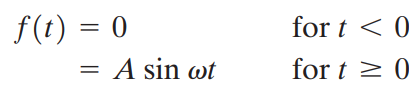
sinusoidal function의 좌극한과 우극한은 다음과 같습니다.
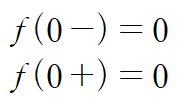
sinusoidal function의 라플라스 변환은 다음과 같습니다.
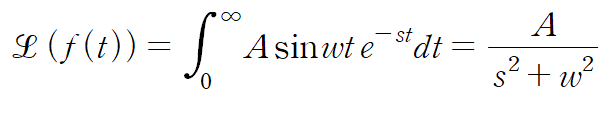
4. Pulse function
Pulse function은 일정 시간동안 상수 인풋을 주는 함수입니다.


pulse function의 좌극한과 우극한은 다음과 같습니다.
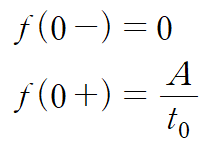
pulse function의 라플라스 변환은 다음과 같습니다.

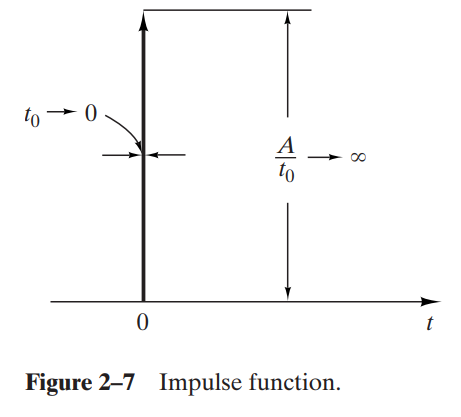
5. Impulse Function
시스템에 짧은 시간 동안 매우 큰 단위의 인풋이 가해질 때 impulse function으로 간주합니다.

impulse function의 좌극한과 우극한입니다.

impulse function의 라플라스 변환입니다.

아래 지수함수의 극한 공식을 사용해 계산합니다.
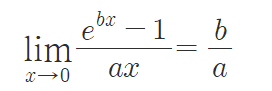
'기계공학 > 4대 역학' 카테고리의 다른 글
| [동역학] 라플라스 변환의 초깃값 정리(Initial-value theorem) (0) | 2022.10.24 |
|---|---|
| [동역학] 라플라스 변환의 좌극한 (lower limit of the Laplace integral), 최종값 정리 (final-value theorem) (0) | 2022.10.23 |
| [유체역학] 가속도장 (Acceleration Field) 유도, 물질도함수 (0) | 2022.10.20 |
| [열역학] 검사체적에서 에너지 방정식 (3) : 과도유동(transient flow process) (0) | 2022.10.01 |
| [열역학] 검사체적에서 에너지 방정식 (2) : 정상상태 유동(steady state flow) (1) | 2022.09.30 |