https://search.shopping.naver.com/book/catalog/32487155058
Linear Algebra and Its Applications, Global Edition : 네이버 도서
네이버 도서 상세정보를 제공합니다.
search.shopping.naver.com
§ 목차 §
0. LU분해 소개
1. LU분해
2. LU분해 알고리즘
3. 파이썬 구현
4. LU분해로 행렬방정식의 해 구하기
5. LU분해로 행렬식 계산하기
0. Introduction
LU분해는 행렬 분해의 한 종류입니다. L은 Lower triangular matrix(하삼각행렬), U는 Upper triangular matrix(상삼각행렬)을 의미합니다. 또다른 행렬 분해로는 직교행렬과 상삼각행렬로 분해하는 QR분해가 있습니다.
QR 분해 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 선형대수학에서 QR 분해(영어: QR decomposition, QR factorization)는 실수 행렬을 직교 행렬과 상삼각 행렬의 곱으로 나타내는 행렬 분해이다.[1] 그람-슈미트 과정이나
ko.wikipedia.org
※ 본 게시글에서는 n x n 행렬에 대한 LU분해만을 다룹니다.
1. LU Factorization
정사각행렬 A에 대한 LU 분해의 정의는 다음과 같습니다.

A를 크기가 n x n 인 정사각행렬인 경우 하삼각행렬 L과 상삼각행렬 U의 곱으로 A가 표현될 수 있다. 이때 A = LU 꼴 표현을 A의 LU분해라 하자.
복잡하게 느껴질 수 있는데 단순히 행렬의 인수분해와 같은 느낌으로 이해하시면 됩니다.
예제를 먼저 보며 LU분해하는 방법을 알아보겠습니다.
(예제 1) 행렬 A에 대해 LU분해를 수행하여라
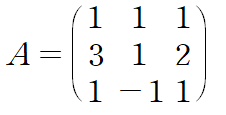
A가 아래 식과 같은 형태의 두 행렬로 분해된다고 가정하겠습니다.
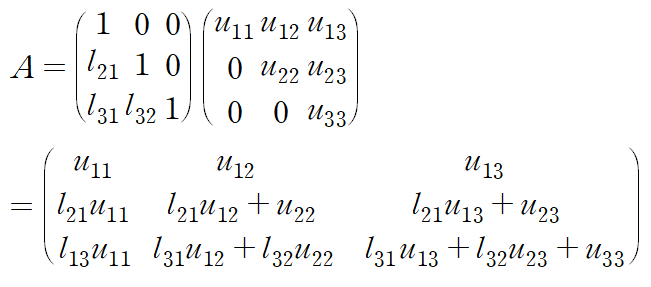
각 요소가 같다는 것을 이용하여 9개의 변수를 결정합니다.
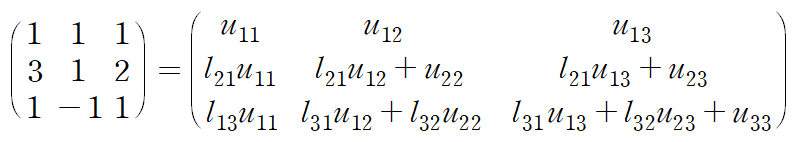
각 성분이 같다는 조건으로부터 행렬 L, U를 구하면 다음과 같습니다.
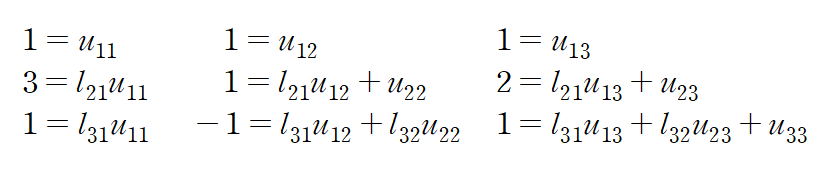
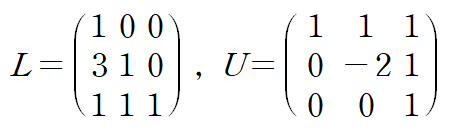
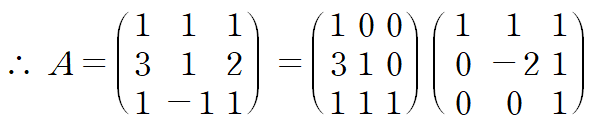
이것은 LU 분해의 한 방법이며 LU분해를 수행하는 여러 가지 방법이 있습니다.
또한 LU분해를 수행했을 때 얻게 되는 두 행렬 L, U는 유일하지 않습니다.
하나의 행렬 A는 다양한 L,U 쌍을 가질 수 있으며 앞선 예제처럼(대각성분이 모두 1) 몇 가지 제약 조건을 주었을 때 유일성을 갖게 됩니다.
2. Algorithm
위 방법을 사용해 LU 분해를 하는 것은 상당히 많은 방정식을 풀어야 하기 때문에 시간도 많이 걸리고 그닥 효율적인 방법이 아닙니다.
다양한 방법으로 LU 분해를 수행할 수 있는데 그 중 대중적으로 사용되는 방법은 "record"를 이용하는 방법입니다.
1. 행렬 A를 상삼각행렬 U로 만드는 행연산(Row addition)을 수행합니다. 이 때 어떤 행연산을 수행했는지 단계별로 기록해야 합니다.
2. 단위행렬 I를 앞서 기록한 행연산에 (-1)을 곱해 동일한 위치에 적용합니다. "이때 단계별로(열 별로) 별도의 행연산, 즉 별도의 단위행렬로부터 행연산을 수행합니다."1번에서 수행한 모든 단계를 거치면 하삼각행렬 L를 얻습니다.
예시로 확인해봅시다.
(예제 2) 2 x 2 행렬 A에 대해 LU 분해를 수행하여라
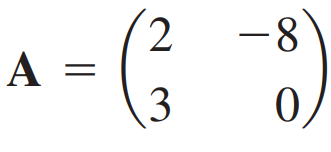
A를 상삼각행렬 U로 만들기 위해서는 첫 번째 행(R1)에 -3/2를 곱해 두 번째 행(R2)에 더해야 합니다. (Row addition 을 수행할 때 cR1 + R2 -> R2 규칙을 따릅니다. 더해지게 되는 행에는 별도의 곱하기를 하지 않습니다. 2R1 + 3R2 -> R2 와 같이 사용하지 않는다는 뜻)
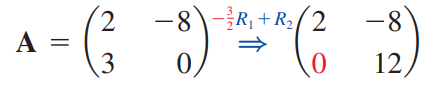
상삼각행렬 U이 만들어졌습니다. 이 -3/2를 기억해두세요.
단위행렬에 앞서 기록된 행연산 (-3/2)에 (-1)을 곱해 하삼각행렬 L을 얻습니다.
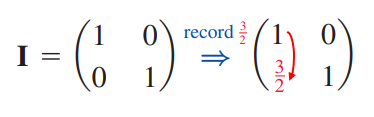
즉 다음과 같이 LU 분해가 수행됩니다.
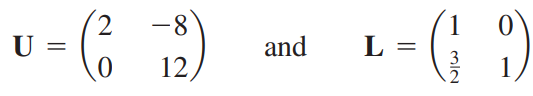
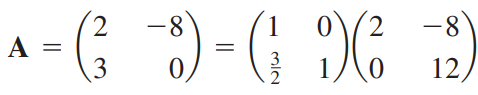
3 x 3 행렬도 마찬가지입니다.
(예제 3) 3 x 3 행렬 A에 대해 LU 분해를 수행하여라
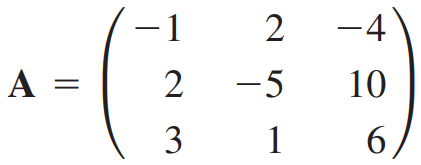
가우스 소거법을 따라 A를 사다리꼴 행렬(Echelon form)으로 만드는 행연산을 수행합니다.
첫 번째 대각성분 -1 아래에 있는 성분을 모두 0으로 만들도록 행연산을 수행하고
그 다음 두 번째 대각성분 -1(정 가운데 있는)의 아래 있는 성분을 0으로 만들도록 행연산을 수행하면
상삼각행렬 U를 얻습니다.
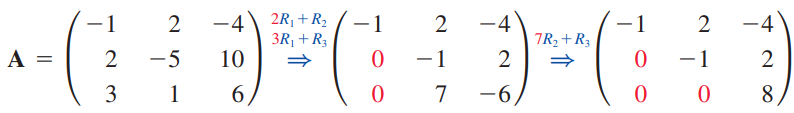
행연산은 두 단계로 진행되었으며, (-1)을 곱한 record들을 사용해 하삼각행렬을 구하면 다음과 같습니다. 처음 이 알고리즘을 소개할 때 "별도의 단위행렬로부터 행연산을 한다"라고 했습니다.
1열의 record는 -2, -3입니다. 이것을 사용해 행연산을 수행하고
2열의 record인 -7을 사용해 행연산을 수행할 때는 단위행렬부터 독립적으로 행연산을 수행한다는 것입니다. 더 쉽게 설명하자면 단순히 현재 pivot인 대각성분 바로 아래부터 record를 써내려가면 된다는 것입니다.
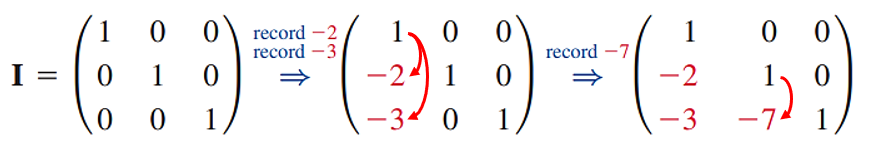
다음과 같이 LU분해가 수행됩니다.
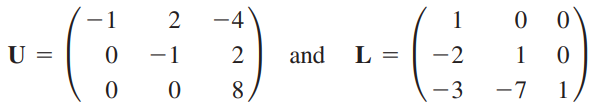
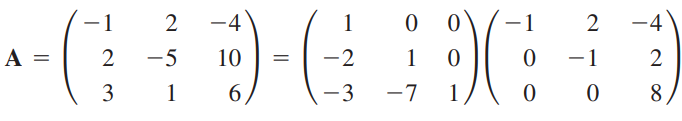
다시 LU 분해 알고리즘을 정리해보겠습니다.
- n x n 행렬 A를 상삼각행렬이 되도록 행연산(Row addition). 1열부터 연산을 거친다. 연산은 1열 : n-1 번, 2열 : n-2 번, . . . , n-1열 : 1번 수행하며 연산 시 사용한 상수(2R1 + R2 -> R2 에서 R1에 곱한 상수 2)를 기록(record)
- n x n 단위행렬 I에 1번에서 사용한 상수들에 (-1)을 곱한 행연산을 수행해 하삼각행렬 U를 얻는다. 이때 주의할 점은 일반적인 행연산처럼 수행하는 것이 아니라 각 단계별로 독립적인 단위행렬 I로부터 행연산을 수행해 합친다. 또는 단순히 현재 pivot인 대각성분 바로 아래부터 record를 써내려간다.
3. Python
위 예시를 파이썬 numpy로 구현할 수도 있습니다.
먼저 행렬 A로부터 상삼각행렬 U를 구합니다.
import numpy as np
a = np.array([[-1,2,-4],[2,-5,10],[3,1,6]], dtype = float)
print(a,"\n") # 행렬 A
# 1열에 대해 기초 행연산
record_1_0 = a[1][0]/a[0][0] # record 추출
a[1] += (-1)*a[1][0]/a[0][0]*a[0]
record_2_0 = a[2][0]/a[0][0]
a[2] += (-1)*a[2][0]/a[0][0]*a[0]
print(a,"\n")
# 2열에 대해 기초 행연산
record_2_1 = a[2][1]/a[1][1]
a[2] += (-1)*a[2][1]/a[1][1]*a[1]
print(a,"\n") # 상삼각행렬 U
> 상삼각행렬 U

하삼각행렬 L를 구하는 방법은 앞서 설명했듯이 별도의 단위행렬로부터 record를 적용하거나 단순히 pivot이 되는 열의 아래에 record를 써내려가면 됩니다.
# 첫 번째 방법 : 행연산 할 때마다 단위행렬 불러오기
I = np.identity(3, dtype = float) # 크기가 3인 단위행렬 I 생성
I[1] += record_1_0*np.identity(3, dtype = float)[0]
I[2] += record_2_0*np.identity(3, dtype = float)[0]
print(I,"\n")
I[2] += record_2_1*np.identity(3, dtype = float)[1]
print(I,"\n") # 하삼각행렬 L
# 두 번째 방법 : 단순히 record가 기록된 위치에 써내려가기
I = np.identity(3, dtype = float)
I[1][0] += record_1_0
I[2][0] += record_2_0
I[2][1] += record_2_1
print(I)
> 하삼각행렬 L

4. Matrix Equation
Ax = b 라는 행렬 방정식(또는 Linear system)에 대해 LU분해를 수행하면 forward-substitution과 back substitution 총 두 단계의 대입과정으로 해를 간단하게 구할 수 있습니다.
LU분해를 행렬방정식(선형방정식)에 적용하여 푸는 방법은 다음과 같습니다.
- Ly = b를 만족하는 y 구하기
- Ux = y를 만족하는 x 구하기
아래와 같은 행렬방정식에서(행렬 A의 크기는 n x n, x의 크기는 n x 1, b의 크기는 n x 1)
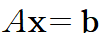
만약 A가 LU분해가 가능하다면
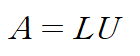
아래와 같이 행렬방정식을 다시 쓸 수 있습니다.
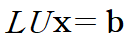
Ux = y라 둔다면(y의 크기는 n x 1)
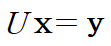
원래 방정식은 아래와 같이 Ly = b를 구하는 문제로 바뀝니다.
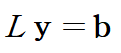
y를 먼저 구하고 그 다음 x를 구합니다.
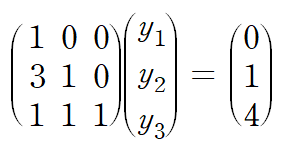
삼각행렬 형태의 행렬로 이루어진 행렬방정식은 위에서부터 아래로 대입하여 해를 쉽게 구할 수 있습니다.
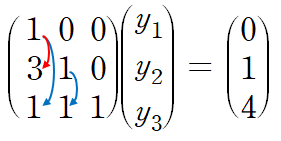
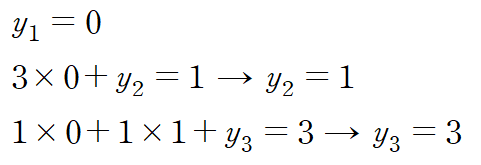
이러한 대입 방식을 forward-substitution이라 합니다.
상삼각행렬의 경우 아래서부터 위로 대입하는 back-substitution을 사용합니다.
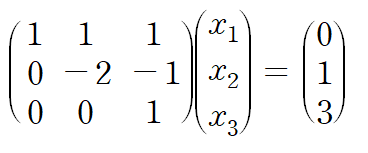
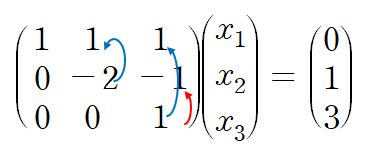
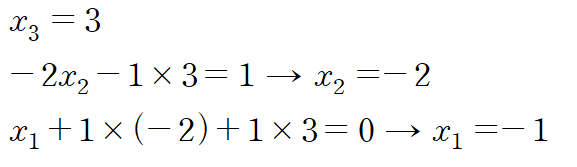
일련의 과정을 종합한 예제를 살펴봅시다.
(예제 4) 연립방정식의 해를 구하여라
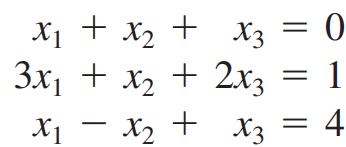
행렬을 사용해 방정식을 표현하면 다음과 같습니다.
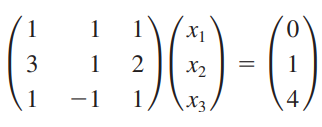
좌변의 행렬에 LU분해를 수행하면 다음과 같습니다.
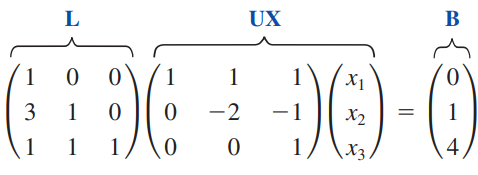
우리가 원하는 건 x이니 Ux = y로 두고 Ly = b 에서 y를 구한 다음 Ux = y를 풀면 됩니다.
1. Ly = b
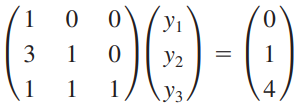
forward-substitution을 사용하여 y를 구합니다.

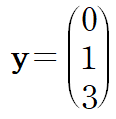
2. Ux = y
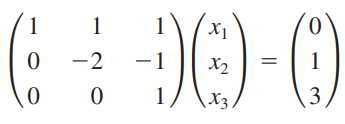
back-substitution을 사용하면 x를 구할 수 있습니다.
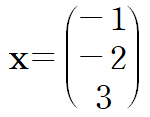
5. Determinant
행렬식의 성질 중 아래와 같은 성질이 있습니다.
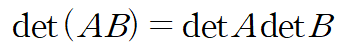
그리고 상삼각행렬 또는 하삼각행렬의 행렬식은 대각성분들을 곱한 것과 같습니다.
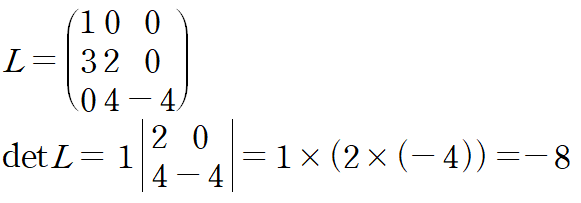
이로부터 행렬 A에 대해 LU분해를 수행해놓으면 단순히 두 삼각행렬의 대각성분들을 모두 곱하는 것으로 A의 행렬식을 구할 수 있다는 것입니다. 이 글에서 소개한 LU분해 알고리즘은 하삼각행렬 L의 대각성분이 모두 1이므로 상삼각행렬 U의 대각성분들을 곱한 것이 A의 행렬식이 됩니다.
(예제 5) A의 행렬식을 구하여라
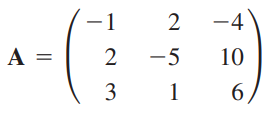
행렬 A에 대해 다음과 같이 LU분해가 가능함을 예제 3에서 확인했습니다.
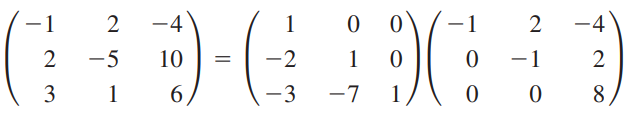
A의 행렬식은 다음과 같습니다.

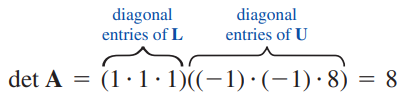
간단히 파이썬으로 구현해봅시다.
이미지 원본 출처 : Advanced Engineering Mathematics 6th Edition by Dennis G. Zill
'MATHEMATICS > 수치해석학' 카테고리의 다른 글
| [수치해석] 비선형 회귀(Nonlinear Regression) 예제, 매트랩 코드 (0) | 2023.07.27 |
|---|---|
| [수치해석] 룽게-쿠타 방법(Runge-Kutta Method), 룽게 쿠타 4차 예제 (0) | 2023.06.08 |
| [수치해석학] 뉴턴-코츠 공식, 심슨 룰(Newton-Cotes Formula, Simpson's Rule) (1) | 2021.12.25 |
| [수치해석학] 뉴턴 보간법 (Newton's Interpolating Polynomial, Divided difference) (0) | 2021.12.16 |
| [수치해석학] 라그랑주 다항식 (Lagrange Polynomial), 파이썬 코드 (0) | 2021.12.08 |