반응형
#재료역학
가스가 든 탱크 등 용기 내의 압력이 외부보다 클 경우 용기에 발생하는 응력은 구형 용기와 원통형 용기로 케이스를 나누어 볼 수 있습니다.
1. Spherical Pressure Vessels
구형 압력용기를 아래 그림과 같이 반으로 잘라보면 중심을 포함하는 단면에서 압력에 의한 힘 P와 응력에 의한 힘 F가 작용합니다.
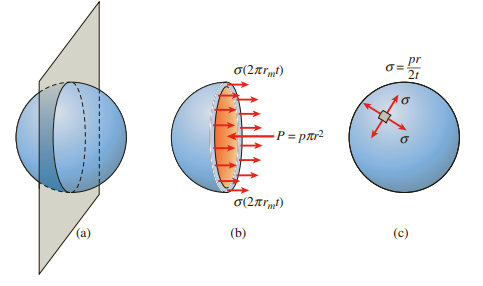
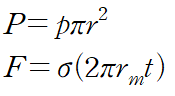
압력에 의한 힘은 압력 X 단면적 이고 응력에 의한 힘은 두께t를 가지는 껍질의 중심까지의 반지름 rm을 사용해 산정하였습니다.
이 두 힘이 평형을 이뤄야 한다는 것에서 용기에 작용하는 응력을 유도할 수 있습니다.
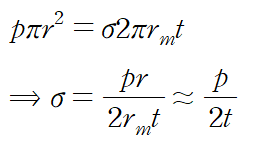
반응형
2. Cylindrical Pressure Vessels
원통형 용기의 경우 원주방향(Circumference) 응력과 축방향(Axial) 응력으로 구분합니다.

원주방향 응력은 위 그림에서 (b)이고, 축방향 응력은 위 그림에서 (c)입니다.
구형 용기와 마찬가지로 평형방정식을 적용해 응력을 구할 수 있습니다.
여기서는 반지름 r과 rm이 큰 차이가 없다고 가정(t가 매우 작은 경우)하였습니다.
> 원주방향 응력
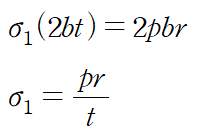
> 축방향 응력
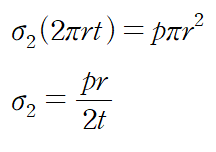
원주방향 응력이 축방향 응력보다 2배가 크다는 것을 알 수 있는데
이는 길이방향 용접강도가 원주방향 용접강도보다 2배 강해야 한다는 것을 의미합니다.
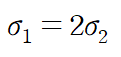
반응형
'기계공학 > 4대 역학' 카테고리의 다른 글
| [유체역학] 버킹엄 파이 정리, 반복변수법 (0) | 2023.02.26 |
|---|---|
| [재료역학] 부정정보 예제 (3) | 2023.02.24 |
| [재료과학] 보의 처짐 예제 (1) | 2023.02.24 |
| [재료역학] 보의 처짐 : 처짐 미분방정식 유도 (Deflections of Beams) (0) | 2023.01.01 |
| [재료역학] 보의 순수 굽힘 - 공식 편 (2) | 2022.12.31 |