1. Conservation of mass
에너지 방정식 이전에, 검사체적에서의 질량유동(유량; 질량유량) 식을 소개합니다.

좌변은 검사체적 내부의 질량의 시간 변화율이고 우변의 첫 번째 항은 들어오는 질량 유동, 두 번째 항은 나가는 질량 유동입니다.
(1) mass flow rate [kg/s]
mass flow rate는 단위시간당 질량의 입출입을 의미하며 아래 관계식이 성립합니다.
(2) volume flow rate [m^3/s]
volume flow rate는 단위시간당 체적의 변화량으로 검사체적에 출입하는 체적이라는 의미를 가집니다.
mass flow rate와 volume flow rate에 대해 다음 관계식이 성립합니다.
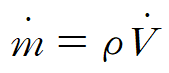
이때 밀도는 질량 / 체적 이며 시간에 따라 변하지 않는다 가정합니다.(출입하는 지점에서의 밀도 변화가 없다고 생각)
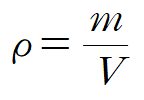
비체적을 사용하면 다음과 같이 나타낼 수 있습니다.
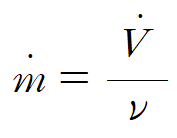
또한 체적을 단면적 A와 질량이 지나간 거리 d의 곱이라 하면 출입 단면적이 일정할 때 다음과 같이 volume flow rate를 나타낼 수 있습니다.
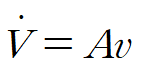
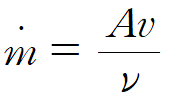
※ 밀도의 단위는 kg / m^3
※ 비체적의 단위는 m^3 / kg
(예제)
공기가 직경 0.2m 의 파이프를 따라 일정한 속도 0.1 m/s 로 유동중이다.
섭씨 25도, 150 kPa의 압력 조건 하에서 질량 유량을 구하여라
Air is flowing in a 0.2m diameter pipe at a uniform velocity of 0.1 m/s.
T = 25°C, P = 150 kPa. What is mass flow rate?
이상기체 방정식으로부터 비체적을 구합니다. (공기의 기체상수는 R = 0.287 kJ/kg·K)
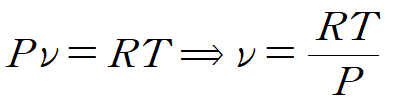

주어진 단면적과 속도를 이용해 mass flow rate를 구합니다.
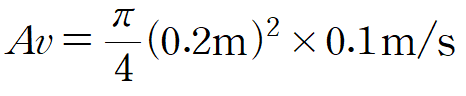
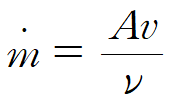
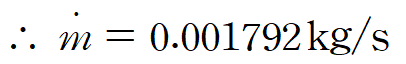
2. Energy equation for a control volume
(1) energy equation for a control volume
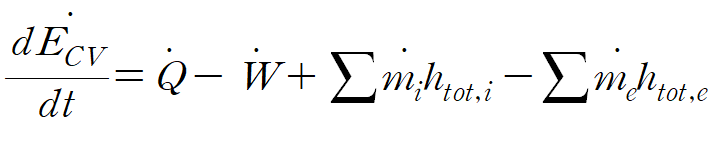
이때 우변의 마지막 두 항을 flow term이라 부릅니다.
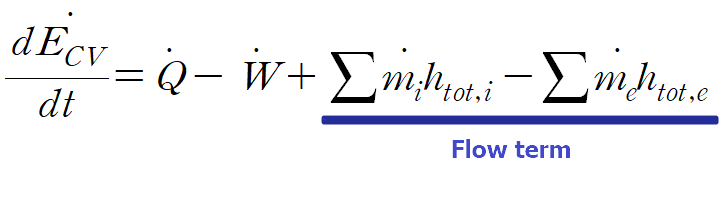
원래 질량유동이 없는 밀폐계에서 에너지 방정식은 flow term 이 없습니다.
flow term은 유동으로 인한 검사체적(control volume) 내부의 에너지를 나타내는 것이며 htot 를 total enthalpy라 합니다.
(2) total enthalpy
total enthalpy는 앞서 말했듯이 출입하는 질량의 에너지를 의미합니다. 다음과 같이 세 항으로 정의됩니다.
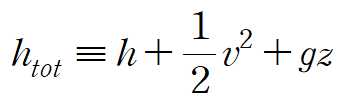
첫 번째 항은 출입하는 질량의 엔탈피, 두 번째 항은 운동에너지(ke), 세 번째 항은 위치에너지(pe)를 의미합니다.
KE라 쓰면 Kinetic Energy를, ke라 쓰면 specific kinetic energy(KE/m) 를 의미합니다. (pe도 마찬가지)
'기계공학 > 4대 역학' 카테고리의 다른 글
| [열역학] 검사체적에서 에너지 방정식 (3) : 과도유동(transient flow process) (0) | 2022.10.01 |
|---|---|
| [열역학] 검사체적에서 에너지 방정식 (2) : 정상상태 유동(steady state flow) (1) | 2022.09.30 |
| [열역학] 이상기체의 엔트로피 변화 (Entropy change for an ideal gas) (0) | 2022.06.06 |
| [열역학] 열역학적 성질들 간의 관계식(The thermodynamic property relation ; gibbs relation) (0) | 2022.06.03 |
| [열역학] 고체, 액체에서의 엔트로피 변화 (0) | 2022.06.01 |