고체, 액체에서 비열(C)을 사용해 엔트로피를 구한 것과는 다르게 기체의 경우 정적비열(Cv0)과 정압비열(Cp0) 두 가지를 사용해 엔트로피 변화를 구할 수 있습니다.
0. Relation, Assumption
이상기체의 엔트로피 변화를 비열로 표현한 관계식은 다음과 같습니다. (결론)
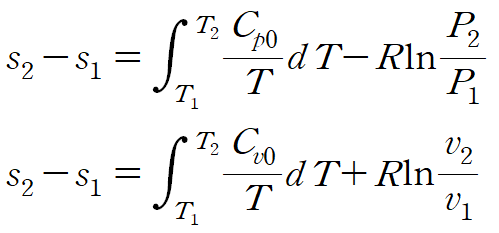
이상기체 방정식, 비열 관계식과 gibbs relation을 사용해 위 식을 유도해보겠습니다.
1. Ideal gas equation

P는 압력, v는 비체적(단위질량당 체적), R은 기체상수, T는 기체의 절대온도입니다.
2. Specific heat relation

원래는 편미분 기호를 사용해야 하지만 내부 에너지 u가 온도 T에만 영향을 받는 함수 u(T)라 가정합니다.
변수분리를 통해 다음과 같이 dh와 du를 나타낼 수 있습니다.
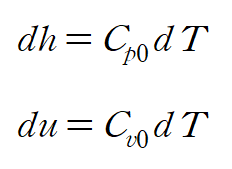
3. Gibbs relation

위 두 식은 gibbs relation입니다. 순물질의 property (P,v,T,h,u,s) 간의 관계를 나타낸 식이며 유도는 아래 글을 참조바랍니다.
https://subprofessor.tistory.com/96
[열역학] 열역학적 성질들 간의 관계식(The thermodynamic property relation ; gibbs relation)
#열역학 0. Relation Thermodynamic property(P,v,T,u,h,s) 간의 관계식은 다음과 같습니다. 1. Energy equation 위 에너지 식으로부터 열역학에서 사용되는 property(P,v,T,u,h,s) 들 사이의..
subprofessor.tistory.com
4. Entropy change for an ideal gas
(1) 정압비열을 이용한 식 유도
gibbs relation 에서 첫 번째 식과 정압비열 식을 사용해 다음과 같이 정리합니다.

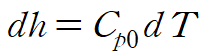
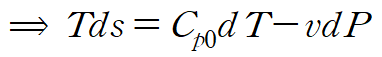
우리가 관심있는 건 ds이므로 양변에 T를 나눠줍니다.

이상기체 방정식을 적용합니다.
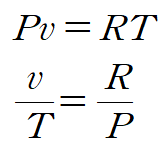

양변을 각 문자에 대해 적분하면 다음과 같이 엔트로피 변화를 표현할 수 있습니다.

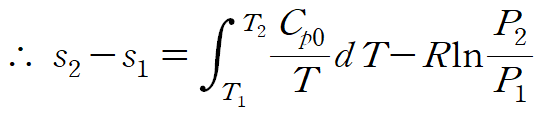
(2) 정적비열을 이용한 식 유도
이번에는 gibbs relation의 두 번째 식과 정적비열 식을 사용합니다.

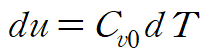
마찬가지로 du를 소거해줍니다.

양변에 T를 나누어줍니다.
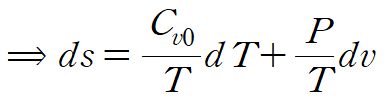
이상기체 방정식을 사용해 정리합니다.
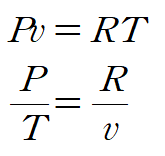

따라서 다음과 같이 이상기체에서 엔트로피 변화를 표현할 수 있습니다.
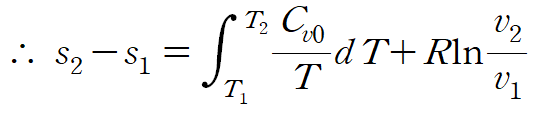
5. Conclusion
이상기체의 엔트로피 변화는 다음과 같이 정압비열과 정적비열로 표현할 수 있습니다.
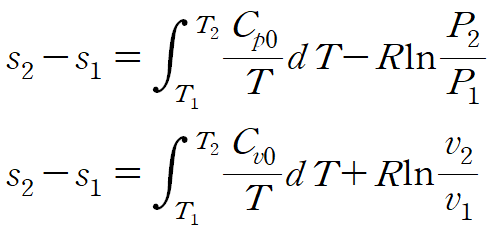
(1) 비열을 상수로 취급할 경우
정적비열과 정압비열을 상수로 취급할 경우 다음과 같이 식을 정리할 수 있습니다.

(2) 사실 두 식은 본질적으로 동일합니다.
정압비열이 정적비열에 기체상수를 더한 것이기 때문에 아래 식을 이용해 두 식이 같은 식이라는 것을 확인할 수 있습니다.

적분형에서 비교해도 되지만 미분형에서 유도해보겠습니다.
정압비열 식에서 시작합니다.

아래 식과 연립하여 식을 정리합니다.



이상기체 방정식에서 양변을 미분소로 표현합니다. (양변 미분)
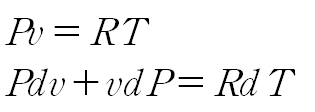
RdT에 위 식을 대입하여 정리합니다.

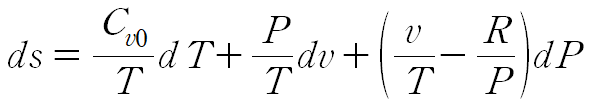
이때 이상기체 방정식으로부터 dP 항이 소거됩니다.
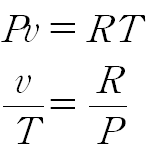
이와같이 정적비열 식을 유도할 수 있습니다.
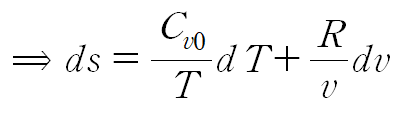
'기계공학 > 4대 역학' 카테고리의 다른 글
| [열역학] 검사체적에서 에너지 방정식 (2) : 정상상태 유동(steady state flow) (1) | 2022.09.30 |
|---|---|
| [열역학] 검사체적에서 에너지 방정식 (1) : 기본 식 설명 (0) | 2022.06.08 |
| [열역학] 열역학적 성질들 간의 관계식(The thermodynamic property relation ; gibbs relation) (0) | 2022.06.03 |
| [열역학] 고체, 액체에서의 엔트로피 변화 (0) | 2022.06.01 |
| [열역학] 압축인자 (Compressibility factor, Z) (0) | 2022.04.30 |