ㄴ
#공업수학
1계 상미분방정식은 네 가지 형태만 알면 됩니다. P(x)dx = Q(y)dy 꼴로 표현가능한 변수분리형과 M(x,y)dx + N(x,y)dy = 0 꼴의 완전미분방정식, y' + P(x)y = r(x) 꼴인 선형 상미분 방정식, y' + p(x)y = r(x)y^a 꼴의 베르누이 방정식.
(1) 변수분리형
https://blog.naver.com/subprofessor/222094390913
[공업수학] 1.3 Separable ODEs (변수분리형 상미분 방정식)
드디어 시작이다. 간단한 변수분리형 1계 상미분 방정식을 풀어보자. 1.2는 방향장(direction field)에 관...
blog.naver.com
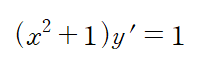
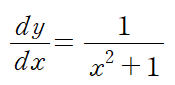
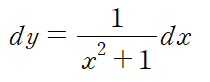
위와 같이 각 변수로만 묶이도록 양변을 정리하여 적분할 수 있는 형태를 변수분리형 미분방정식이라 합니다.
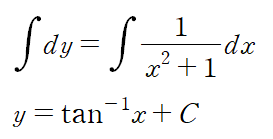
※ 적분상수는 양변에 모두 쓸 필요 없고 마지막에 우변에만 하나 써주면 됩니다.
푸는 방법을 정리하면
(1) 양변을 x, y 각각의 문자들만 모이게끔 정리한다.
(2) dy와 dx를 분리해 P(x)dx = Q(y)dy 꼴로 정리한다.
(3) 양변을 각각의 문자로 정리해 y = f(x)를 얻는다.
(2) 완전 미분 방정식
https://blog.naver.com/subprofessor/222094820066
[공업수학] 1.4-1 완전미분방정식(Exact ODEs)
슬슬 WOWOWOW 할 수준이 슬금슬금 보인다. 오늘 배울 완전미분방정식의 기반을 이루는 개념은 편미...
blog.naver.com
다음과 같이 x, y 두 변수로 이루어진 함수 u가
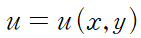
아래 관계식을 만족한다고 생각해봅시다.
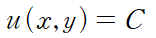
양변을 미분한다고 생각해보면 일단 우변은 0이 되고, u에 대한 전미분은 다음과 같습니다.
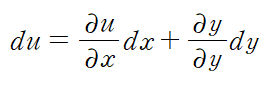
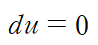
즉 아래와 같은 식을 얻게 됩니다.
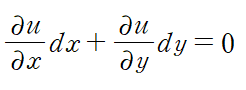
편의상 x에 대한 편도함수를 M, y에 대한 편도함수를 N이라 합시다.
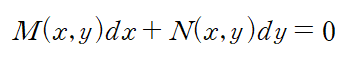
클레로 정리에 의해, u의 이계도함수가 연속이라면 f_xy = f_yx가 성립합니다.
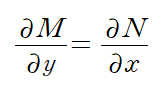
따라서 Mdx + Ndy = 0 꼴의 미분방정식에서 dx 앞의 항과 dy 앞의 항을 각각 y, x에 대해 미분했을 때 같은 결과가 나온다면 그 해는 u(x,y)=C꼴로 나타낼 수 있다는 것입니다. 또한 M와 N은 u의 편도함수라는 의미에서 연관성이 생기구요.
완전미분방정식을 푸는 방법을 정리하면 다음과 같습니다.
(1) 완전성 검사 : M을 y에 대해 편미분한 것과 N을 x에 대해 편미분한 것을 비교한다.
(2) u = int(M) dx +k(y) 로 설정. 또는 u = int(N)dy + k(x) 로 설정.
(3) u의 편도함수가 N임을 (M임을) 이용해 k(y) 또는 k(x)를 결정한다.
(4) u = C꼴의 해를 정리한다.
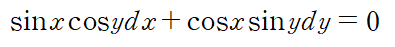
dx 앞에 있는 것이 M이고 dy 앞에 잇는 것이 N이므로
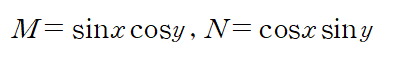
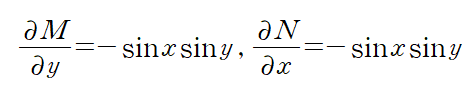
따라서 완전성을 만족함을 알 수 있습니다.
x에 대한 u의 편미분이 M이므로 다음과 같이 u를 설정할 수 있습니다.
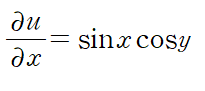
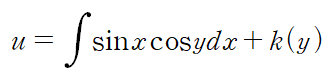
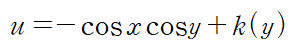
양변을 편미분하고 아래 식에 대입하여 k 를 결정합니다.
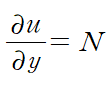
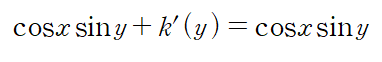
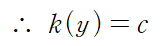
이때 u(x,y) = C 이므로 해는 다음과 같이 음함수 형태로 표현됩니다.
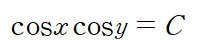
(3) 선형 상미분 방정식
1계 선형 상미분 방정식은 다음과 같이 변수분리가 불가능한 형태의 미분방정식입니다.
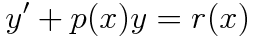
푸는 방법은 간단합니다.
(1) y'+p(x)y =r(x) 꼴 표준형으로 정리하고 적분인자를 구한다.
(2) 양변에 적분인자를 곱한다. (좌변이 적분인자와 y의 곱으로 정리됨)
(3) 양변을 적분해 y = f(x)꼴 해를 얻는다.
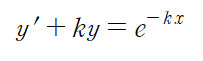
적분인자를 곱해주어 좌변을 정리해주면 쉽게 풀립니다.
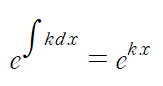
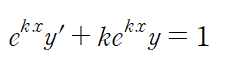
이때 좌변이 적분인자와 y의 곱을 미분한 형태이기 때문에
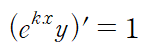
양변을 x에 대해 적분하면 해를 구할 수 있습니다.
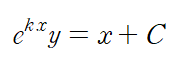
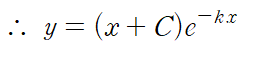
※ 처음 적분인자를 구할 때 적분상수는 등장하지 않습니다. 마지막 적분할 때만 적분상수를 넣어주면 됩니다.
(4) 베르누이 방정식
베르누이 방정식은 선형 상미분 방정식의 형태와 유사하지만 r(x)에 y^a 가 곱해져있는 비선형 방정식입니다.
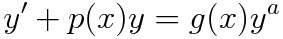
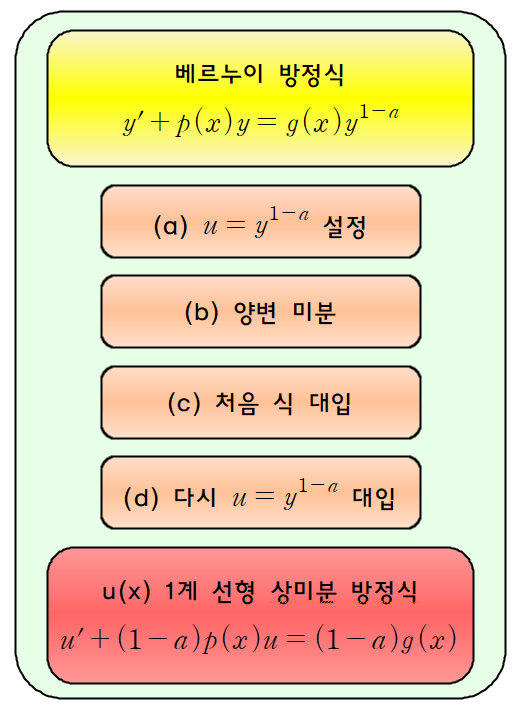
베르누이 방정식을 푸는 방법은 다음과 같습니다.
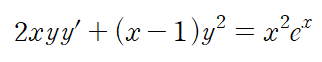
미분방정식을 풀 때 일반적으로 가장 먼저 해야 할 것은 표준형으로 정리하는 것입니다.
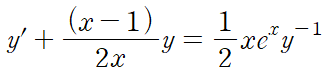
a = -1 인 베르누이 방정식을 얻습니다.
u를 설정하고 양변을 미분합니다.
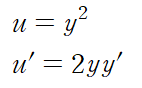
처음식에서 y' 를 정리해 u'에 대입합니다.
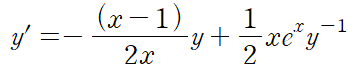
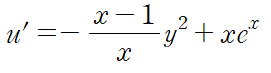
이때 y^2 = u이므로 선형 상미분 방정식 형태로 정리됩니다. (무조건 치환되고 소거되는 형태로 정리됩니다.)
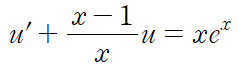
이제 정리된 선형 상미분 방정식을 풉니다. 적분인자를 구하고 양변에 곱해 정리합니다.
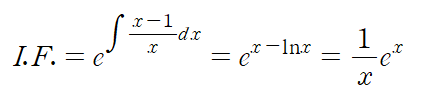
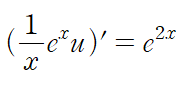
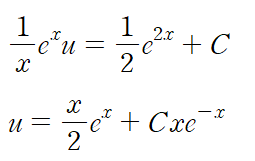
이때 u = y^2 이었으므로
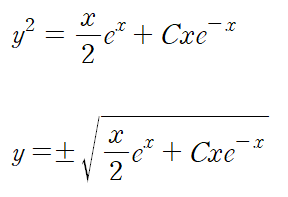
우변의 부호는 초깃값이 주어지면 결정됩니다.
Any Qustions, Any Comments are WELCOME :)
오타나 오류 지적 감사히 받습니다
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] *편미분 방정식 예제 : 라플라스 변환* (0) | 2022.06.17 |
|---|---|
| [공업수학] 1계 상미분방정식 총정리 (2) : 동차방정식(제차방정식), u = ax+by+c 꼴 치환 (0) | 2022.03.21 |
| [공업수학] 코시 적분 정리와 공식 (Caychy's Integral Theorem, Formula) (0) | 2021.12.19 |
| [공업수학] 코시-리만 방정식(Cauchy-Riemann Equations) 예제 (2) | 2021.12.07 |
| [공업수학] 12. 푸리에 사인 급수, 푸리에 코사인 급수 (0) | 2021.04.16 |