1. 코시-리만 방정식 (Cauchy-Riemann Equations)

z = x + yi 인 복소공간에서 f(z) = u(x,y) + i v(x,y) 가 연속이고 미분가능하면 u, v는 아래 방정식을 만족합니다.

위 방정식을 코시-리만 방정식이라 부릅니다.
즉 f(z)가 정의역 D에서 해석적(analytic)이라면 D의 모든 점에서 f(z)의 편도함수가 존재하고 코시-리만방정식을 만족합니다.
2. 증명
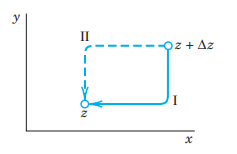
복소함수는 어느 방향으로 Δz 를 잡더라도 미분계수가 존재할 때 미분가능합니다.
따라서 x, y 두 방향으로의 f(z) 미분계수를 따져봅시다.
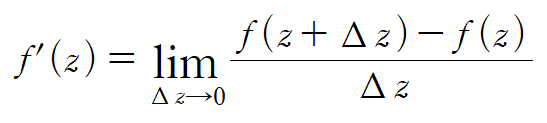
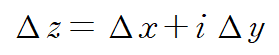
Δx와 Δy를 이용해 f'(z)를 표현합니다.
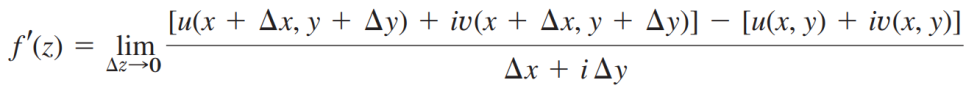
이때 1번 경로는 Δy=0 인 경우니까 1번 경로에 대한 임의의 점 z에서의 미분계수는 아래와 같습니다.
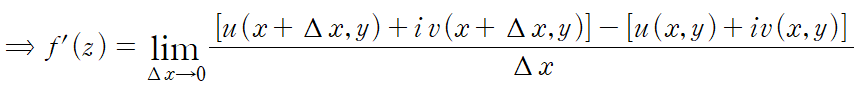
따라서 x축과 평행한 방향으로 접근했을 때 미분계수는 아래와 같습니다.
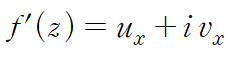
2번 경로의 경우 Δx=0 이므로
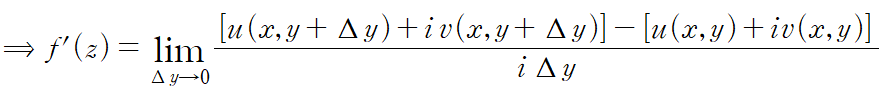
y축과 평행한 방향으로 접근했을 때 미분계수는 아래와 같습니다.
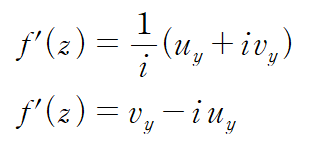
f'(z)를 실수부와 허수부로 나눴을 때 f(z)가 미분가능하다면,
1번 경로의 실수부 = 2번 경로의 실수부에서
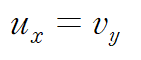
1번 경로의 허수부 = 2번 경로의 실수부에서
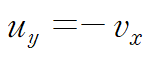
따라서 미분가능하다는 조건(f(z) is analytic)과 코시-리만 방정식이 성립함은 필요충분조건이 됩니다.
3. 예제
(예제 1) f(z)가 해석적인지 판별하여라
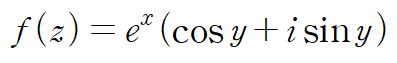
먼저 실수부와 허수부를 나눕니다.
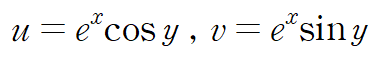
코시-리만 방정식으로부터 다음 식이 성립합니다.
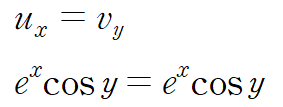
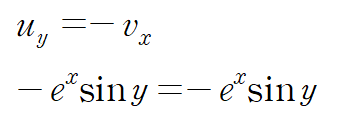
코시-리만 방정식이 성립하므로 f(z)는 해석적입니다.
(예제 2) f(z)가 해석적이고, 실수부 u가 다음과 같을 때 f(z)를 구하여라
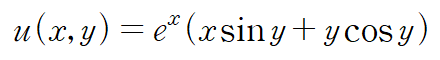
문제에서 원하는 함수는 아래와 같은 형태의 f(z)입니다.
f(z)가 해석적이니, 코시-리만 방정식이 성립합니다.
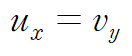
로부터 vy 는 다음과 같습니다.
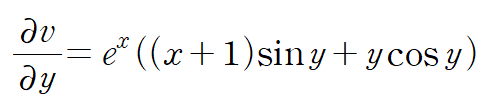
양변을 y에 대해 적분을 취해 v를 얻을 수 있습니다. 이때 x는 편미분 할 때처럼 상수취급합니다.
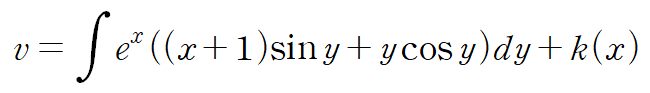
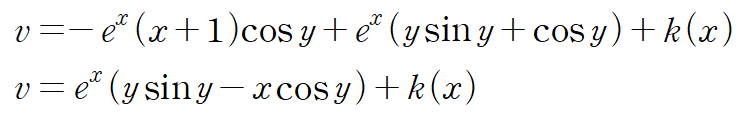
얻은 v를 x에 대해 편미분합니다.
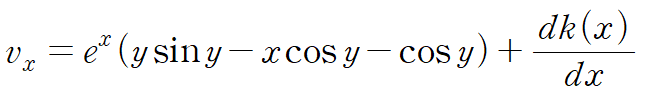
코시-리만 방정식의 두번째 식을 적용합니다.
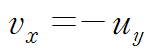
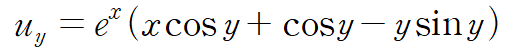

위 식으로부터 k(x)를 확정합니다.
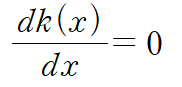
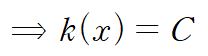
f(z)의 허수부는 다음과 같습니다.
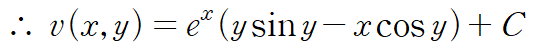
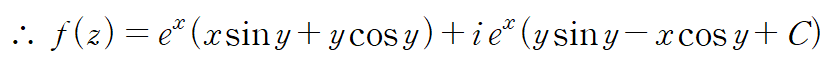
(예제 3) f(z)가 해석적이고, 실수부 u가 다음과 같을 때 f(z)를 구하여라. 단 f(0)=0
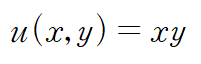
첫 번째 코시-리만 방정식으로부터
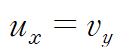
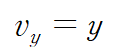
양변을 y에 대해 적분합니다.
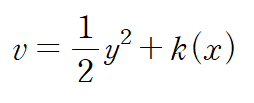
두 번째 코시-리만 방정식을 적용하여 허수부 함수 v(x,y)를 구합니다.
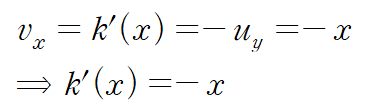
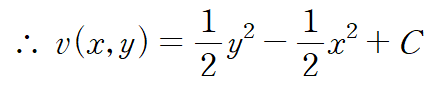
f(z)는 다음과 같습니다. (f(0)=0 조건을 적용)
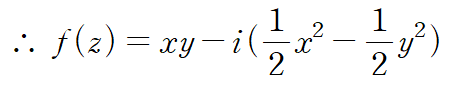
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 1계 상미분방정식 총정리 (1) : 변수분리형, 완전미분방정식, 선형 상미분 방정식, 베르누이 방정식 (1) | 2022.03.19 |
|---|---|
| [공업수학] 코시 적분 정리와 공식 (Caychy's Integral Theorem, Formula) (0) | 2021.12.19 |
| [공업수학] 12. 푸리에 사인 급수, 푸리에 코사인 급수 (0) | 2021.04.16 |
| [공업수학] 11. 편미분 방정식 : 1차원 파동방정식 유도 (0) | 2021.03.27 |
| [공업수학] 10. 라플라스 변환의 미분과 적분 (0) | 2021.03.01 |