영어로는 "Differentiation and Integration of Transforms"
t-domain 함수 f(t)에 라플라스 변환을 취한 s-domain 함수 F(S). F(s)를 s에 대해 미분하거나 적분했을때 어떤 관계식이 성립하는지 알아봅시다
(i) Definition
(1) 라플라스 변환의 미분
라플라스 변환 F(s)에 대해 다음 관계식이 성립합니다.
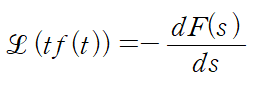
<증명>
f(t)에 대한 라플라스 변환을 F(s)라 합시다

라플라스 변환의 정의에 따라 F(s)는 아래와 같이 이상적분으로 정의됩니다.
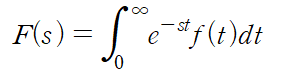
양변을 s에 대해 미분하면 아래와 같은 관계식을 얻습니다.
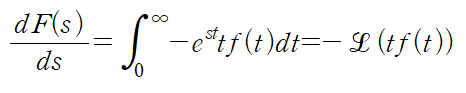

역변환을 취하면 다음과 같습니다.

(2) 라플라스 변환의 적분
f(t)에 대한 라플라스 변환 F(s)은 다음 관계식을 만족합니다. s~는 문자의 혼동을 피하기 위해 사용한 것입니다. 합성곱 포스팅에서 나온 τ(tau)와 같은 역할입니다.

<증명>
이것 또한 라플라스 변환의 정의를 이용해 유도할 수 있습니다.
정의에 따라 F(s~)을 정적분 형태로 전개하면 아래와 같습니다.

이중적분 형태로 정리되는데, 구간을 바꿔도 무방합니다. 해서 다음과 같이 정리할 수 있습니다.

안쪽에 있는 s~부터 적분해줍니다

따라서 다음과 같이 정리되며
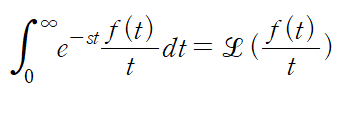
식이 유도됩니다
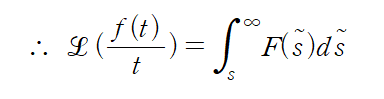
(ii) Application
미분 공식과 적분공식은 일반적인 라플라스 변환을 취하기 어려운 f(t)에 대해 변환을 수행하거나, 주어진 F(s)를 미분하여 보다 쉽게 역변환을 구하는 용도로 사용됩니다.
예제 1 : 다음 f(t)에 대하여 라플라스 변환을 구하여라

두 가지 방법으로 라플라스 변환을 구해보겠습니다. 첫 번째 방법은 s-shifting을 이용한 방법입니다. e^kt가 곱해져있으니, t^n 의 라플라스 변환에 s-shifting theorem 을 적용해주면 됩니다.
혼동이 없도록 g(t)를 설정해주겠습니다.


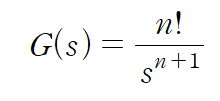

두 번째 방법은 오늘 배운 F(s)의 미분 공식을 사용하는 것입니다.
이번에는 t^n이 아니라 e^kt에 포커스를 맞춥니다.
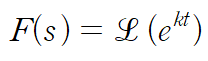
양변을 미분합니다. 미분 공식에 의해 아래와 같은 관계식을 얻습니다.

한 번 더 미분해줍시다.

이에, F(s)를 s에 대해 n번 미분하면 아래와 같은 관계식이 성립함을 알 수 있습니다.

우리가 구하고자 하는 t^n e^kt에 대해 정리합시다
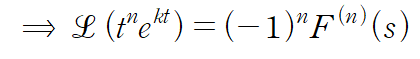
이제 F(s)를 n번 미분한 결과를 대입해주면 끝나겠지요
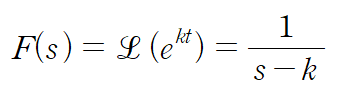
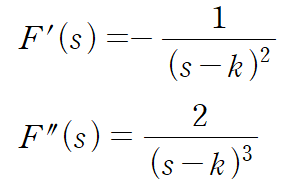
마찬가지로 n번 미분해준 결과를 정리합시다

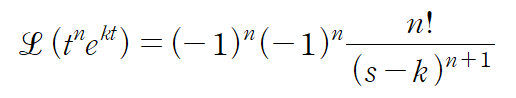
(-1)이 두개 곱해져 있으니, 모든 n에 대하여 상쇄됩니다. 따라서 다음과 같이 라플라스 변환이 이루어짐을 알 수 있습니다.

예제 2 : 다음 F(s)에 대하여 라플라스 역변환을 구하여라

먼저 F(s)를 미분하기 쉬운 형태로 바꾸겠습니다.
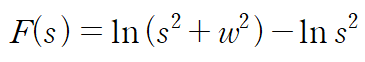
s에 대해 양변을 미분합니다
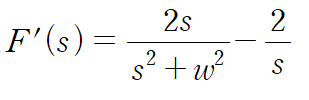
양변에 역변환을 취하면 다음과 같습니다.
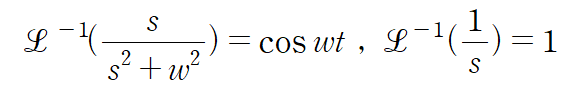

이때, 미분공식에 의하여 다음이 성립합니다


따라서 F(s)의 역변환은 다음과 같습니다.
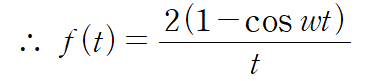
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 12. 푸리에 사인 급수, 푸리에 코사인 급수 (0) | 2021.04.16 |
|---|---|
| [공업수학] 11. 편미분 방정식 : 1차원 파동방정식 유도 (0) | 2021.03.27 |
| [공업수학] 9. 적분방정식(Integral Equation) (0) | 2021.03.01 |
| [공업수학] 8. 합성곱(convolution) (2) | 2021.03.01 |
| [공업수학] 7. 디랙 델타, Short Impulse (0) | 2021.02.18 |