#재료역학
#고체역학
보의 전단력이 작용하고 있을 때 단면의 y지점에서 발생하는 전단응력은 다음과 같습니다.
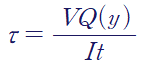
V는 단면에 작용하는 전단력
y는 중립축(도심)으로부터의 거리
Q(y)는 y지점에서 "바깥쪽 단면에 대한 단면 일차 모멘트"
I는 중립축 기준 단면 이차 모멘트(Iz 또는 Iyy). 모든 지점에서 동일한 값
t는 y지점에서의 가로폭. y지점마다 다를 수 있음.
응용하는 예제를 한 번만 따라가면 공식을 어떻게 적용하는지 바로 감을 잡을 수 있습니다.
예제를 통해 . . .
> 복잡한 형상의 단면 이차 모멘트
> 단면 일차 모멘트(Q)를 쉽게 구하는 방법
> 전단응력의 분포
등을 익히게 됩니다.
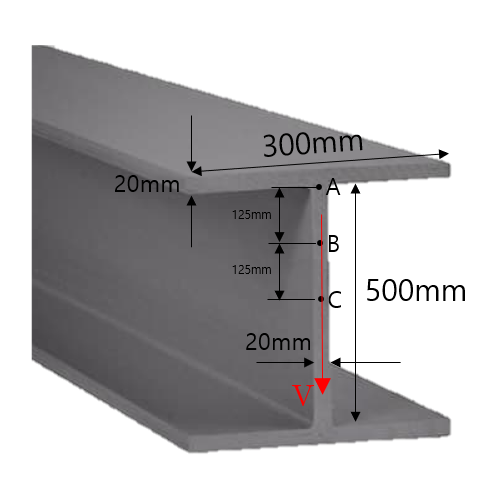
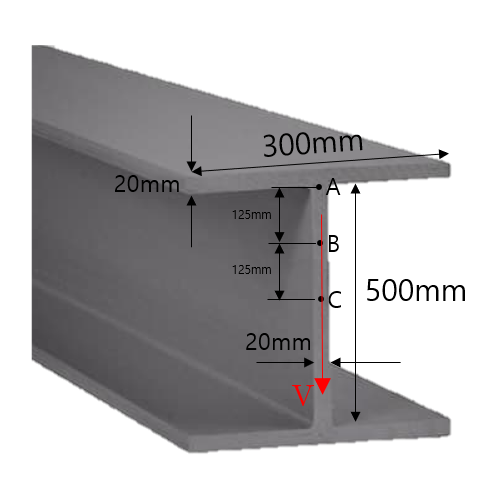
(예제) WF보에 V = 10kN의 전단력이 작용할 때, 점 A, B, C에서의 전단응력을 구하여라
C점은 도심이다.
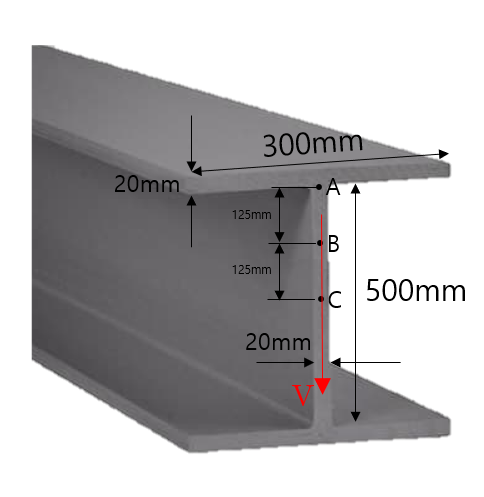
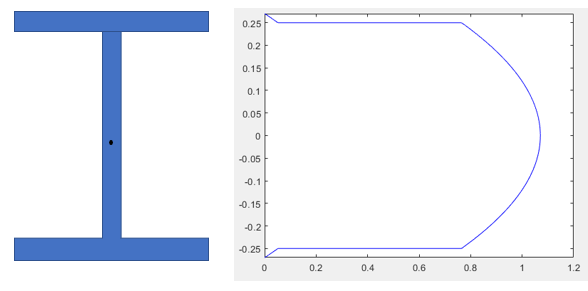
> WF보(Wide-Flange Beam / Web-Flange Beam)
WF보는 중심부Web과 상,하단의 대칭적인 Flange로 구성되어있는 구조물입니다.
> A,B,C점에서 전단응력 구하기
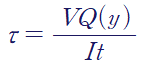
문제에서 전단력V를 주었고, 폭t는 A,B,C점 모두에서 20mm(0.02m)입니다.
복잡한 형상의 단면 이차 모멘트
간단한 형상들의 단면 이차 모멘트는 다음과 같습니다.
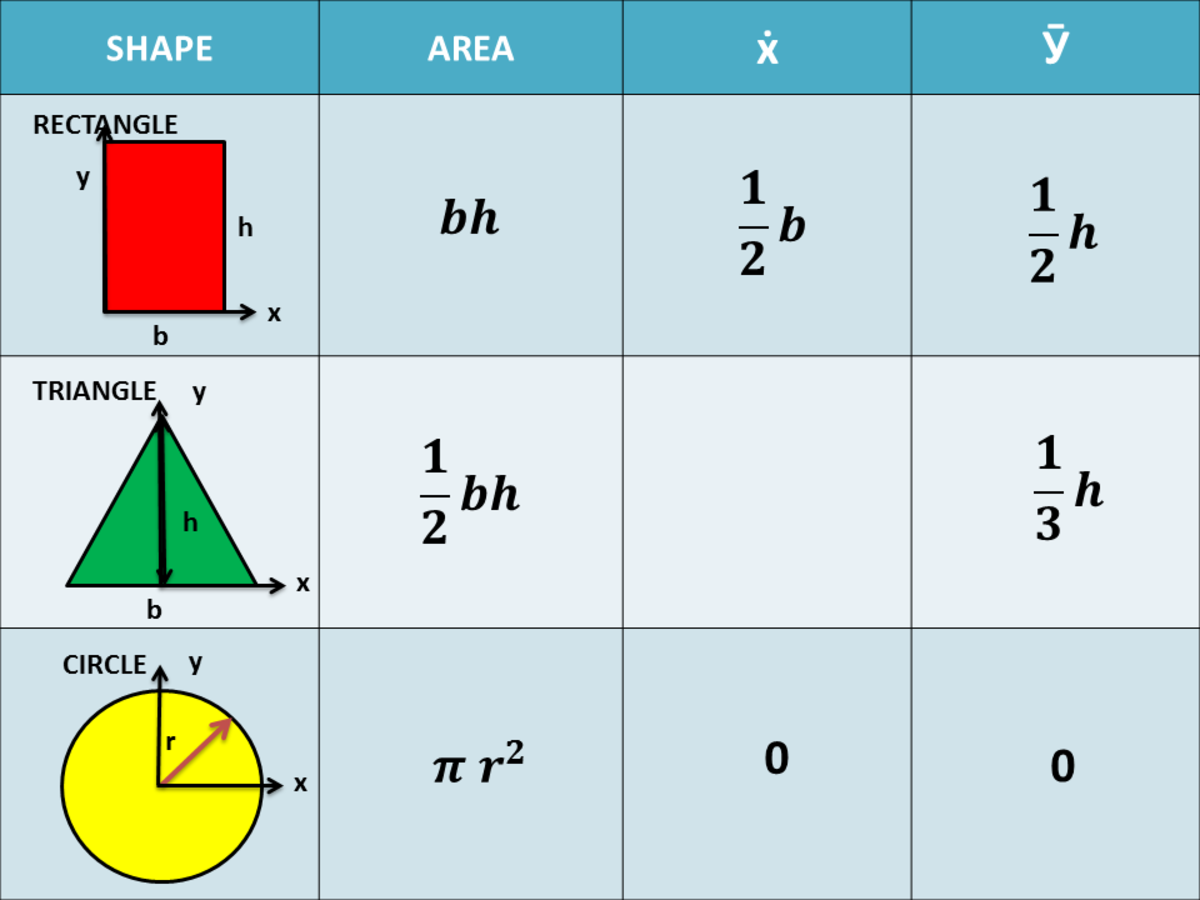
직사각형, 원같이 간단하지 않은 복합 단면에서의 단면 이차 모멘트는 크게 두 가지 테크닉으로 계산할 수 있습니다.
[1] 간단한 단면들로 나누어 계산 후 합치기
[2] 큰 단면에서 없는 부분을 빼기
WF보의 경우 Web의 I와 Flange의 I를 각각 구해 더해주거나, 큰 직사각형 단면에서 양옆 사이드를 제거했다고 보는 거죠
[1] 간단한 단면들로 나누어 계산 후 합치기
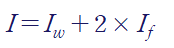
web)
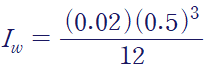
flange)
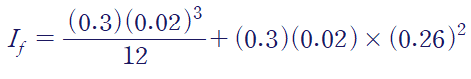
평행 축 정리 (Parallel Axis Theorem)
1. 평행 축 정리 (Parallel Axis Theorem) 평행축 정리는 단면 2차 모멘트를 평행 이동된 다른 좌표계에 대해서 구할 때 유용하다. H beam이나 I beam과 같이 복잡한 단면 형상의 경우 간단한 사각형으로 나
satlab.tistory.com
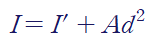
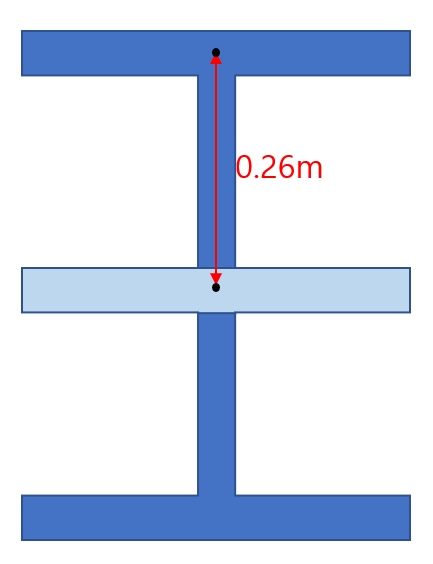
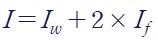
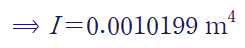
이렇게 구한 단면 이차 모멘트는 전체 큰 직사각형에서 양옆 사이드를 빼어 구한 것과 동일합니다.
[2] 큰 단면에서 없는 부분을 빼기
아래 그림처럼 큰 직사각형에 대하여, 양옆 사이드의 초록 부분을 뺍시다.

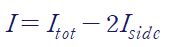
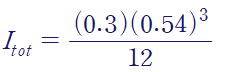
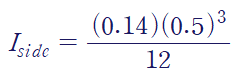
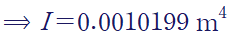
[1],[2] 어떤 방법을 사용하여도 같은 단면 이차 모멘트를 구할 수 있습니다.
첫 번째 방법은 직관적이라는 장점이 있지만 평행축정리를 사용해야 한다는 단점이,
두 번째 방법은 평행축정리를 사용하지 않아도 된다는 장점이 있습니다.
단면 일차 모멘트 Q
이제 마지막으로 남은 것은 "바깥쪽" 단면 일차 모멘트 Q를 계산하는 것입니다.
단면 일차 모멘트Q는 다음과 같이 정의됩니다.
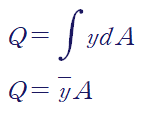
두 번째 식에서 y_bar가 의미하는 것은 전체 단면의 도심으로부터 계산하고자하는 단면의 도심까지의 거리입니다.
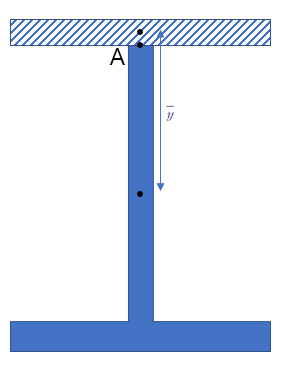
바깥쪽이라고 하는 것은 도심으로부터 바깥쪽 면적을 말합니다.
A의 경우 아래와 같은 빗금친 부분이 바깥쪽 면적이 되겠죠
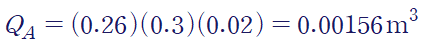
B의 경우 복합 단면이니, 각각의 단면 일차 모멘트를 분리해서 계산한 다음 합산합니다.
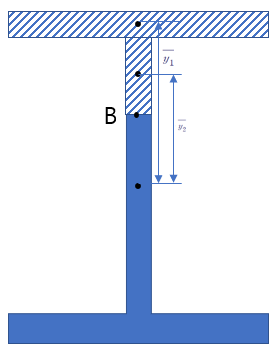
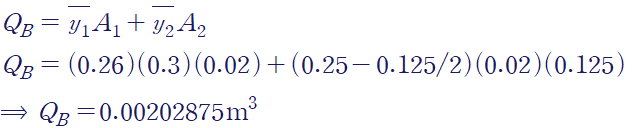
C도 마찬가지로 구해줍니다.
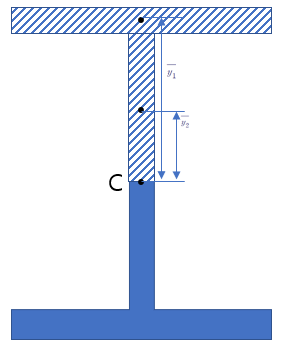
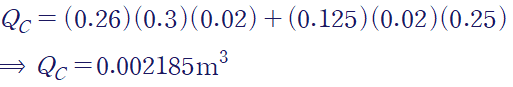
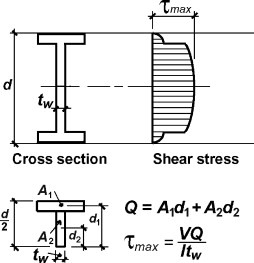
전단응력
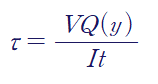
점 A,B,C에서의 전단응력은 다음과 같습니다.
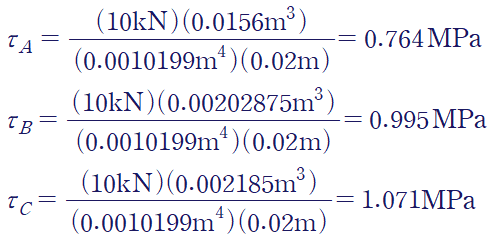
도심 근처로 갈수록 전단응력이 커짐을 볼 수 있습니다.
☆통상적으로 도심에서 전단응력이 최대입니다.
단면에서 y값에 따른 전단응력 분포는 이차곡선의 형태를 가집니다.
전단응력 그래프 라는 용어는 없지만 아래와 같이 표현할 수 있겠습니다.
저희도 이와 같은 그래프를 표현해봅시다.
(i) 0.25<y<0.27
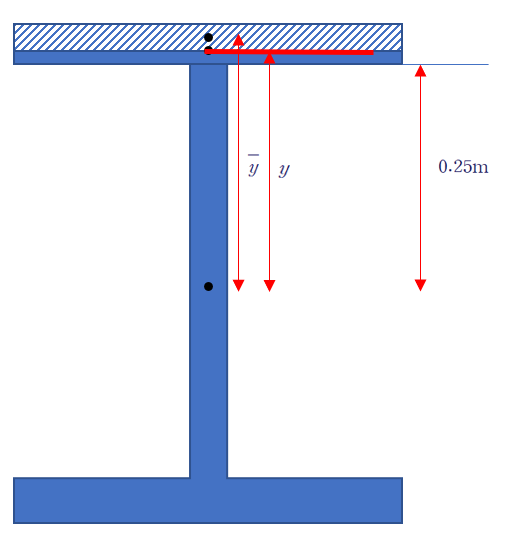
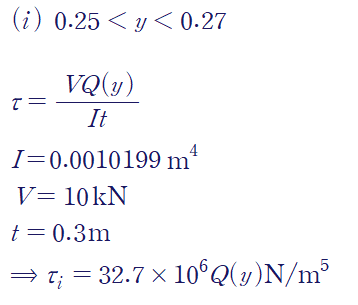
Q(y)를 계산해야 하는데, 바깥쪽 단면의 도심은 직사각형 요소의 바깥점(0.27)과 안쪽점(y)의 중점이므로, 둘을 더해 2로 나누어 계산할 수 있습니다.
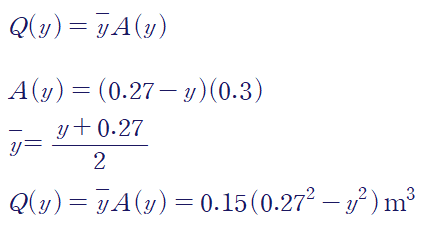
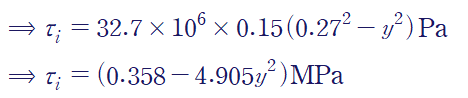
(ii) 0<y<0.25 의 경우도 마찬가지로 표현할 수 있습니다.
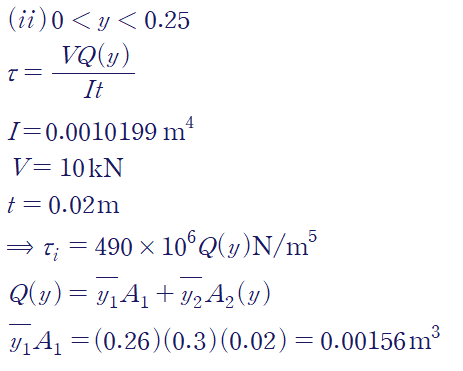

이상의 결과를 나타내면 다음과 같습니다.
'기계공학 > 4대 역학' 카테고리의 다른 글
| [유체역학] 개수로 유동(Open Channel Flow) 예제 : Specific Energy (0) | 2024.10.12 |
|---|---|
| [유체역학] 나비에-스톡스 방정식의 무차원화 (0) | 2024.10.08 |
| [유체역학] 블라시우스 해법(Blasius Solution) 유도 (0) | 2024.06.13 |
| [재료역학] 모어 원 그리는 법(Morh's Circle) (0) | 2024.06.12 |
| [유체역학] 운동량 적분 방정식 유도(Momentum Integral Equation) (1) | 2023.10.06 |