위가 뚫려 있는 (Open Channel) 상황인 개수로 유동에서 유체 흐름의 구동력은 중력입니다.
에너지 관계식(베르누이 방정식)
속도 프로파일이 V1, V2로 각 단면에서 균일하다고 합시다.
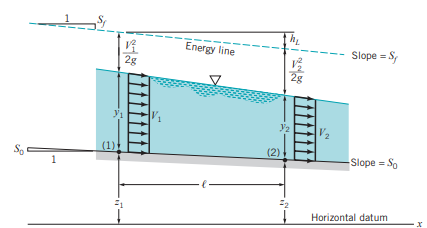
1지점 상단(공기와 맞닿는 표면)과 2지점 상단에 베르누이 방정식을 적용하면 다음과 같습니다.
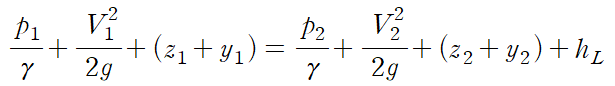
여기서 1지점과 2지점 모두 대기압으로 사라지고
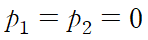
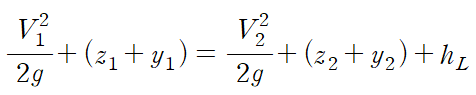
수로의 경사(기울기)를 S0(bottom slope)라 하면 z1-z2= S0l 입니다.
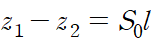
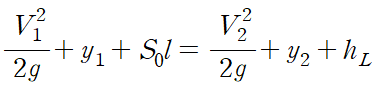
수로 표면과 마찰로 인해 발생하는 수두 손실 hL(head Loss)은 관의 길이(l)에 비례하므로
Sf(friction slope)를 이용하여 다음과 같이 나타낼 수 있습니다.
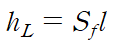
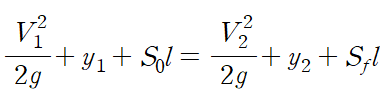
식을 정리하면 다음과 같습니다.
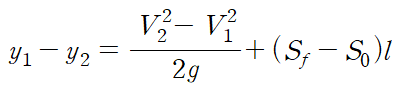
기울기와 마찰로 인한 손실을 무시하는 경우
기울기와 마찰로 인한 손실을 무시하는 경우, 다시말해 Sf = S0 = 0인 상황입니다.
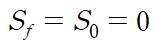
앞서 정리한 에너지 관계식은 다음과 같이 간단하게 표현이 됩니다.
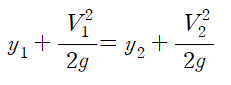
<단위폭당 유량(Flowrate per unit width)>
유량 Q를 폭 b(width)로 나눈 것을 단위폭당 유량 q라 합니다.
즉 q = Q/b입니다.
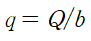
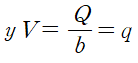
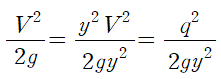
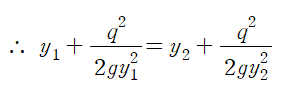
위와 같은 유도과정을 거쳐 표현한 것을 (Specific Energy)라 합니다.
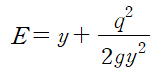
여기서 E의 단위는 일반적인 에너지의 단위가 아니라 길이(m)입니다.
즉 우리는 "기울기와 마찰로 인한 손실을 무시하는 경우"에 E1 = E2라는 관계식을 쓰겠습니다.
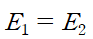
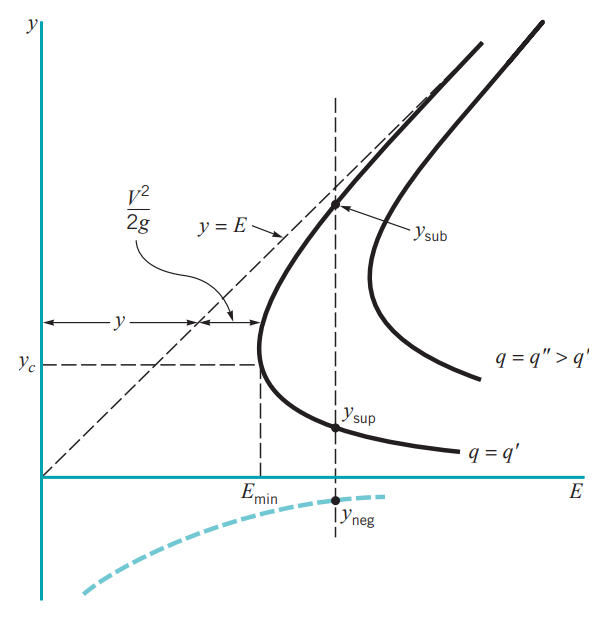
고정된 E값에 대해 가능한 y값의 양상은 위와 같습니다.
같은 E값에 대하여 실수 y는 보통 두 개가 존재하게 되는데
큰 값을 subcritical depth(condition), 작은 값을 supercritical depth(condition)이라 합니다.
한국어로는 각각 상류 수심, 하류 수심입니다.
Example
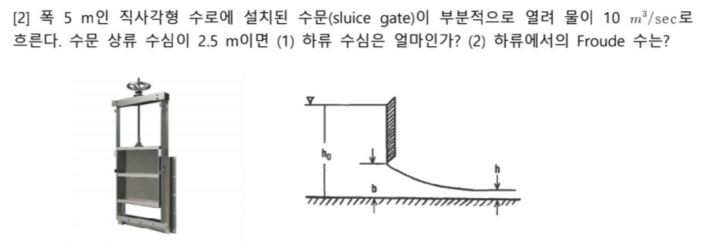
실제로는 수문을 지나가는 부분에서 에너지 손실이 있지만, 여기서는 무시하고 계산하겠습니다.
(1) 하류 수심은 얼마인가?
상류에서의 Spicific Energy가 하류에서와 동일하다고 합시다.
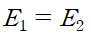
중요한 것은 "유량과 수심을 알고 있으면 Specific Energy를 계산할 수 있다는 것"입니다.
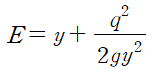
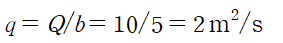
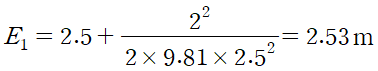
E2를 알기 위해 식을 정리하고
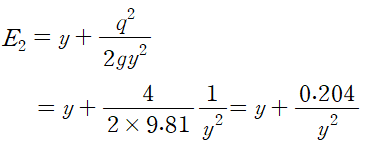
E1 = E2 = 2.53m를 적용하면
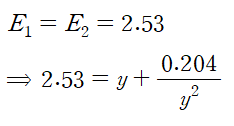
삼차방정식을 얻게 됩니다.
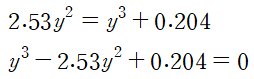
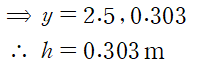
하류 수심은 0.303 m 입니다.
(2) Froud 수의 정의는 다음과 같습니다.
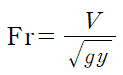
하류에서의 유속(V)은 다음과 같습니다.
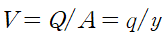
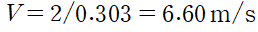
따라서 하류에서의 Froud 수는 다음과 같습니다.
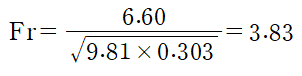
'기계공학 > 4대 역학' 카테고리의 다른 글
| [재료역학] 보의 전단응력 예제(WF보) (0) | 2024.10.21 |
|---|---|
| [유체역학] 나비에-스톡스 방정식의 무차원화 (0) | 2024.10.08 |
| [유체역학] 블라시우스 해법(Blasius Solution) 유도 (0) | 2024.06.13 |
| [재료역학] 모어 원 그리는 법(Morh's Circle) (0) | 2024.06.12 |
| [유체역학] 운동량 적분 방정식 유도(Momentum Integral Equation) (1) | 2023.10.06 |