블라시우스 해법은 평판 위를 흐르는 정상, 비압축성 층류 경계층 방정식의 고전적 해법입니다. 이를 유도하기 위해 몇 가지 단순화와 변환 과정을 거칩니다. 자세한 유도 과정을 아래에 설명합니다.
지배방정식(Governing Equation)
2차원 정상, 비압축성 흐름을 위한 나비에-스토크스 방정식은 다음과 같습니다:

경계층 가정(Boundary Layer Assumptions)
평판 위 경계층 흐름의 경우:

이러한 가정에 따라 경계층 방정식은 다음과 같이 단순화됩니다 :

유사 변환(Similarity Transformation)
위 방정식을 풀기 위해 유사 변환을 사용합니다. 유사 변수 η(eta) 와 유동함수(stream function) ψ(psi) 를 도입합니다 :

여기서 U는 자유흐름 속도입니다
유동함수(stream function) ψ는 다음과 같이 속도 성분 u와 v와 관련됩니다:

유동함수(stream function)를 이 관계식에 대입하면:

운동량 방정식에 대입
유사 변수와 유동함수(stream function)를 단순화된 운동량 방정식에 대입하면:

u와 v를 대입하면:

정리하면, η가 소거되고 블라시우스 방정식이 유도됩니다:

경계 조건(Boundary Conditions)
문제의 경계 조건은 다음과 같습니다:

해법과 결론(Solution and Conclusion)
블라시우스 방정식은 3차 비선형 상미분 방정식으로, 일반적으로 수치적으로 풀립니다. RK 4th method를 사용해 풀 수 있고, 그 해는 이미 구해져 있습니다.
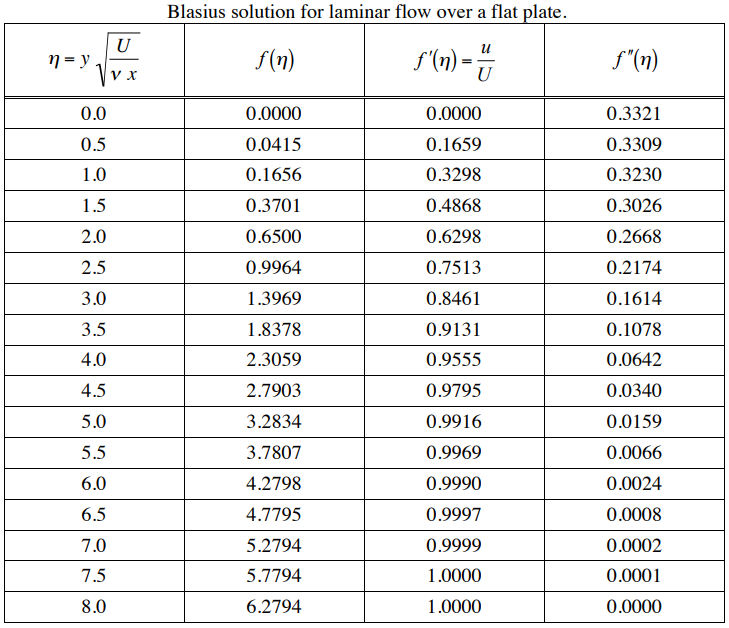
블라시우스 해법은 평판 위 층류 경계층 흐름에 대한 속도 분포를 제공하며, 경계층이 선단에서부터 거리의 제곱근에 따라 어떻게 성장하고, 속도가 벽에서 자유흐름 속도로 어떻게 전이하는지를 설명합니다.
'기계공학 > 4대 역학' 카테고리의 다른 글
| [유체역학] 개수로 유동(Open Channel Flow) 예제 : Specific Energy (0) | 2024.10.12 |
|---|---|
| [유체역학] 나비에-스톡스 방정식의 무차원화 (0) | 2024.10.08 |
| [재료역학] 모어 원 그리는 법(Morh's Circle) (0) | 2024.06.12 |
| [유체역학] 운동량 적분 방정식 유도(Momentum Integral Equation) (1) | 2023.10.06 |
| [유체역학] 항력계수(Drag Coefficient) (0) | 2023.08.09 |