#고체역학
#재료역학
모어 원
모어 원은 원하는 임의의 경사면 요소에 대하여 응력 상태를 쉽게 알 수 있게 해주는 유용한 도구입니다.
"평면응력 상황에서" 주로 사용되며
모어 원을 그리게 되면 재료에 작용하는 최대,최소 수직응력 그리고 최대전단응력을 한 눈에 살펴볼 수 있다는 큰 장점이 있습니다.
수업을 하다보면 많은 학생분들이 어려워하는 부분인데
사실 한,두 번 정확히 그리다보면 쉽게 익숙해질 수 있는 파트입니다.



모어 원 그리는 법
모어 원 그리는 방법은 간단합니다.
1. 삼각형을 그린다. 이때, 빗변이 원의 반지름(R)이 되고 각도는 2θp이다.
2. 원의 중심(Center)를 구한다.
3. 모어 원을 그리고, 시작점을 표시한다.
아래와 같은 응력 상황을 보겠습니다.

1. 삼각형을 그린다.

이 삼각형의 가로와 세로는 응력들을 이용해 정의되어 있으며
삼각형을 그리는 목적은 빗변이자 모어 원의 반지름이 되는 R을 구하기 위함입니다.
여기서 삼각형의 왼쪽 각은 주각(θp)의 두 배입니다.
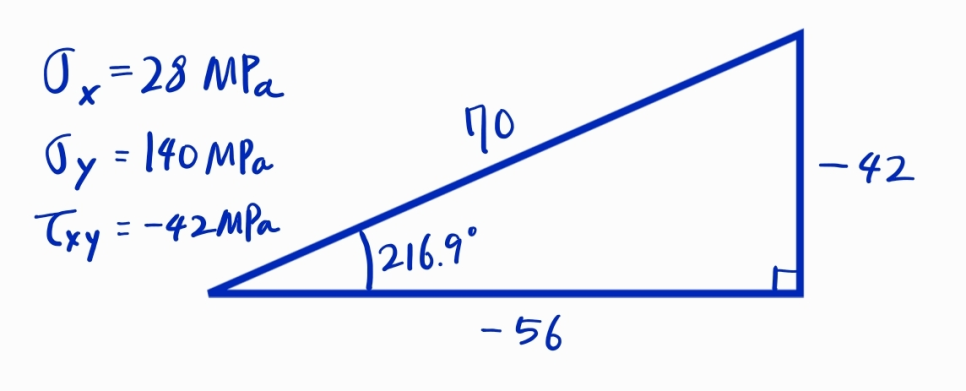
반지름 R = 70이고, 주각(Principal Angles)은 216.9/2 = 108.4가 됩니다.
2. 원의 중심을 구한다.
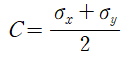
위 식을 이용하면 C = 84 입니다.
3. C와 R을 가지고 모어 원을 그립니다.
이때 중심은 항상 가로축 위에 있습니다.
아래 그림은 일반적인 상황의 모어 원을 그린 겁니다.
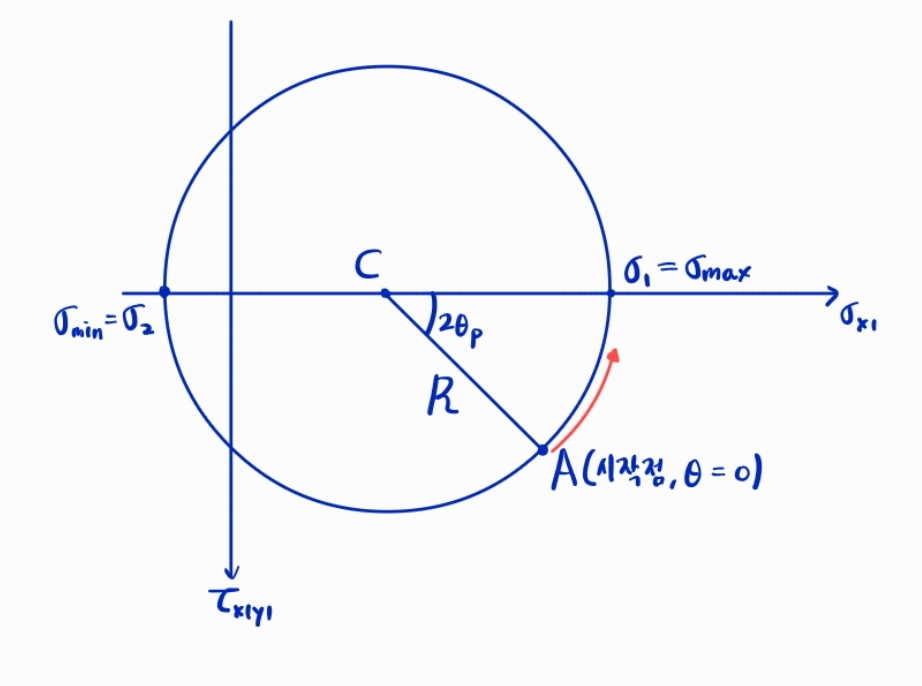
★ 주각은 "현재 상태에서 최대 수직응력을 갖기 위해서 회전해야 하는 각도"를 의미합니다.
1, 2의 결과를 가지고 모어 원을 그리면 다음과 같습니다.
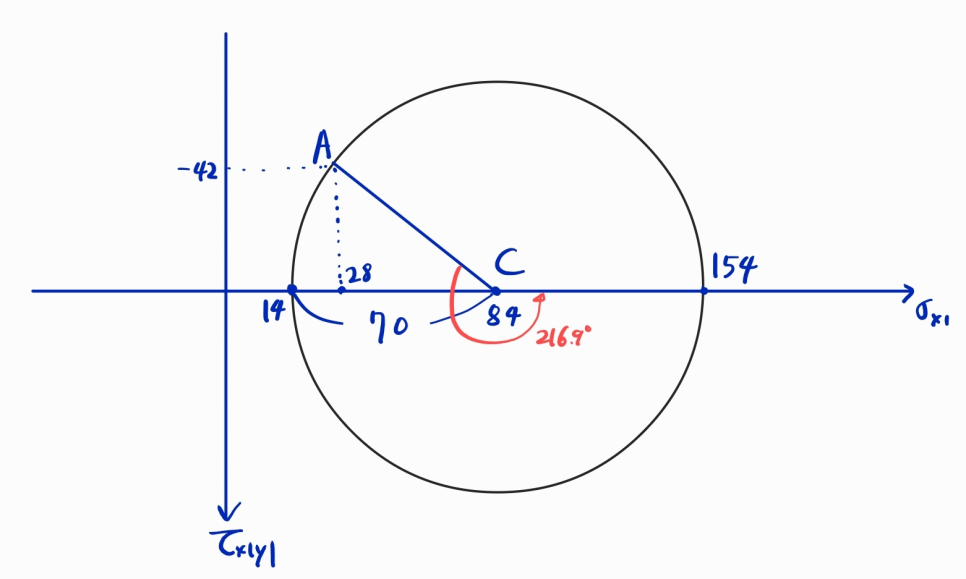
주각을 가지고 시작점 A를 표시하기 어렵다면, 단순히 초기상태에서 응력을 좌표처럼 생각해서 A점을 구할 수 있습니다.
<모어원에서의 규칙>
1. 각도 단위는 2θ, 반시계 방향으로 회전
2. 전단응력 축은 아래를 향하도록
3. 중심은 항상 수평축 위에
이게 끝입니다.
핵심은 반지름, 중심, 시작점입니다.
문제에서 주로 요구하는 것
1. 주응력(최대,최소 수직응력)과 최대전단응력(R)
2. 주각(Principal Angles) 또는 주축(Pricipal Axis)을 구하여라
3. 각도 θ 만큼 회전한 응력 요소 그리기
4. 주응력 상황에서 응력 요소 그리기
1.
주응력은 모어원을 그리게 되면 수평축과 만나는 지점을 쉽게 찾을 수 있는데(C+R, C-R)
그 두 값을 주응력이라 합니다.
앞서 예시로 든 상황에서 주응력은 다음과 같습니다.
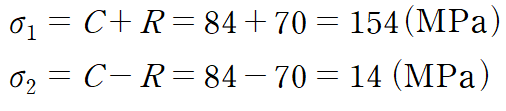
최대 전단응력은 모어원 그림에서도 알 수 있듯이 원의 반지름과 같습니다.
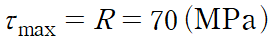
2.
주각은 삼각형의 각도/2입니다.
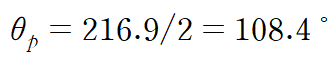
3.
가령, 반시계 방향으로 30도 회전한 요소의 응력을 구한다 합시다.
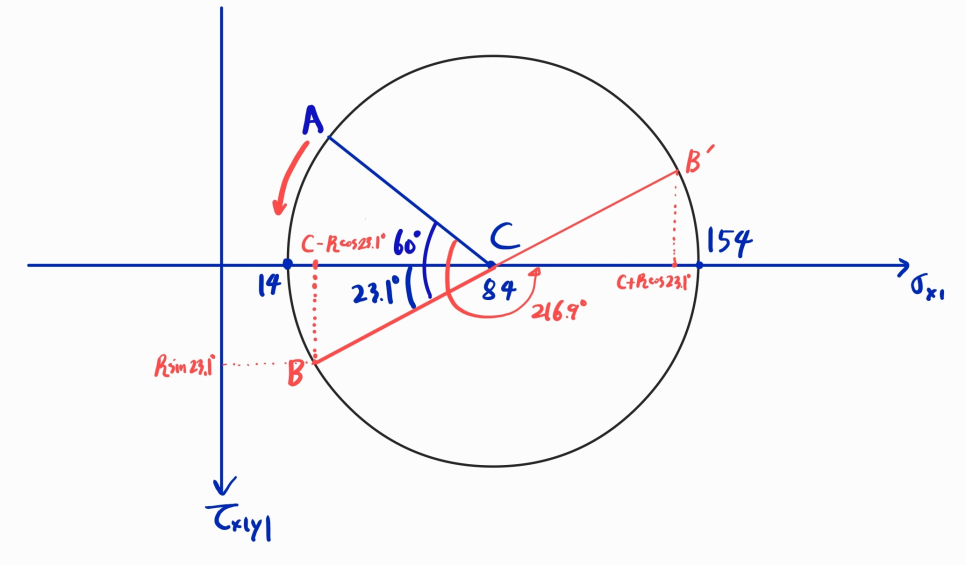
모어원에서는 각도 단위가 2θ가 되기 때문에 이를 꼭 주의해주시구요
B점을 회전한 상태라 한다면, 위와 같은 그림에서 응력을 구하는 것은 너무나 쉽습니다.
또 주의해야 할 것은 수직응력이 2개이기 때문에, 거기서 90도 회전한(모어원 상에서는 180도) B'점의 응력을 구해서 표시해줘야 합니다.
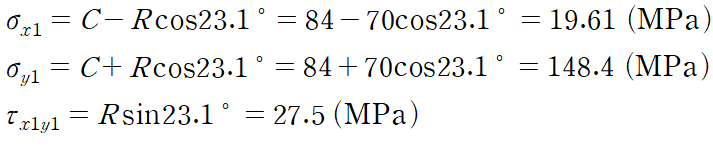
전단응력 축이 아래 방향이라는 것도 주의해주세요
4.
주응력 상황에서는 전단응력이 없습니다.
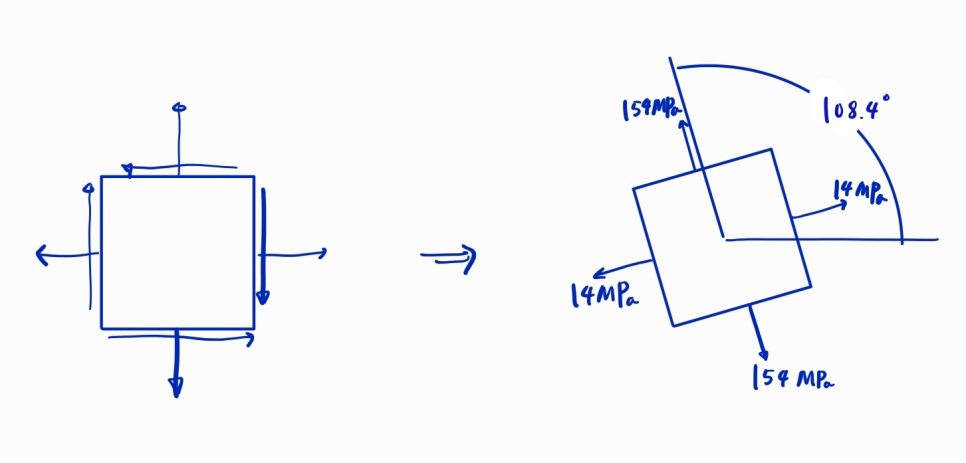
주각만큼 회전한 면(축)에 최대 수직응력을, 수직인 면에 최소 수직응력을 쓰면 됩니다.
'기계공학 > 4대 역학' 카테고리의 다른 글
| [유체역학] 나비에-스톡스 방정식의 무차원화 (0) | 2024.10.08 |
|---|---|
| [유체역학] 블라시우스 해법(Blasius Solution) 유도 (0) | 2024.06.13 |
| [유체역학] 운동량 적분 방정식 유도(Momentum Integral Equation) (1) | 2023.10.06 |
| [유체역학] 항력계수(Drag Coefficient) (0) | 2023.08.09 |
| [유체역학] 수력도약(Hydraulic Jump) (0) | 2023.08.05 |