#유체역학
#무차원화
목차
1. 차원과 단위(Dimensions and Units)
2. 방정식의 무차원화(Nondimensionalization of Equations)
3. 예제1 : 운동방정식 - 중력가속도
4. 무차원화의 장점
5. 예제2 : 나비에-스톡스 방정식(Navier-stokes equation)
6. 특수한 경우들
1. 차원과 단위
무차원화(Nondimensionalization)을 이해하기 위해서는 먼저 차원의 정의를 알아야 합니다.
정의 : Dimension is a measure of physical quantity while a unit is a way to assign a number to that dimension.
예를 들어 "길이"는 차원이고, 미터(m)나 인치(inch)는 단위가 됩니다.
Length : Dimension(L)이고 이에 대응되는 unit은 m, km, cm, inch, ft . . .
주요한 7가지 차원(Primary dimensions)으로 존재하는 모든 물리량을 표현할 수 있습니다.
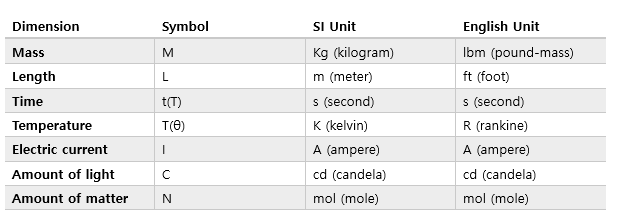
예를 들어 밀도의 경우 아래와 같이 M,L로 표현할 수 있습니다.
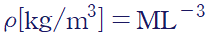
2. 방정식의 무차원화
방정식의 각 항의 차원이 없을 때(dimensionless) 무차원 방정식(nondimensional equations)이라 합니다.
(1) 무차원 변수
무차원 변수의 정의는 다음과 같습니다.
Quantites that change or vary in the problem, but have no dimensions.
예를 들어 우리가 푸는 수학 문제들은 대부분 무차원 방정식입니다.
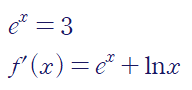
(2) 방정식의 무차원화
다음 세 가지 순서로 진행됩니다.
1. 적절한 Scaling parameters를 선정
2. 무차원 변수를 정의
3. 기존의 방정식을 무차원화
3. 예제 1 : 운동방정식 - 중력가속도
다음과 같은 운동방정식을 생각해봅시다.
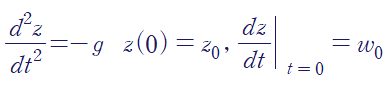
초기위치와 초기속도가 각각 z0, w0으로 주어진 z방향 운동방정식입니다.
현재 중력만이 외력으로 작용하고 있어, F=ma에서 질량 m을 소거한 형태로 주어졌습니다.
이 방정식의 해는 아래와 같습니다.
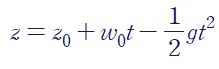
그렇다면 위 운동방정식의 차원은 무엇일까요?
어떤 방정식의 차원을 쉽게 파악하는 방법은 양변의 차원이 같다는 것입니다.
우변이 중력가속도인데, 가속도의 차원은 m/s^2이므로 주어진 방정식의 차원은 다음과 같습니다.
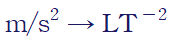
1. 적절한 Scaling parameters를 선정
scaling parameter는 방정식을 무차원화하기 위해 방정식의 양변에 곱해거나 나눠줄 parameter를 말합니다.
여기서는 초기값으로 주어진 z0와 w0를 사용합시다.
2. 무차원 변수를 정의
방정식을 구성하고 있는 변수인 z와 t가 무차원 변수가 되도록 각 차원에 맞추어 나눠줍니다.
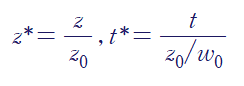
이때, 무차원 변수를 정의하는 것은 문제를 푸는 사람의 자유입니다.
그렇지만, 통상적으로 어떤 상황에서 어떻게 무차원변수를 정의하는지 정해져 있으며
공부를 조금만 하면 감을 익힐 수 있습니다.
z는 z0로 나누어 주었는데 t는 t0로 나누지 않은 이유?
> t0라는 것이 따로 정의된 것도 아니고 크게 어떤 의미를 갖지 못하기 때문에 거리를 속도로 나눈 z0/w0로 t를 나눠줍다.
3. 기존의 방정식을 무차원화
앞서 정의한 무차원 변수들을 주어진 방정식에 대입합니다.
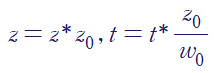
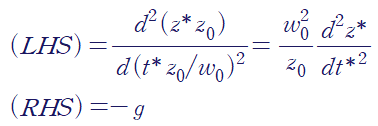
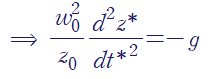
이를 정리하면 아래와 같이 양변이 무차원인, 무차원 방정식을 얻을 수 있습니다.
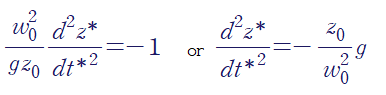
프루드 수(Fround number)를 다음과 같이 정의하면
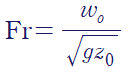
간단하게 무차원 방정식을 표현할 수 있습니다.
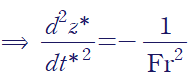
무차원 방정식의 해를 구하면 다음과 같습니다.
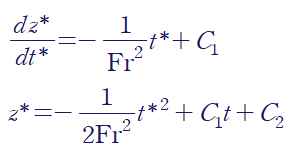
C1, C2를 구하기 위해 초기조건을 사용해야 하는데, 주어진 초기조건으로 무차원화된 초기조건을 사용합시다.
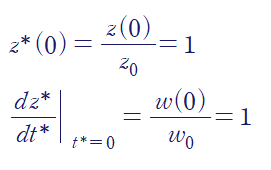
따라서 다음과 같은 해를 얻습니다.
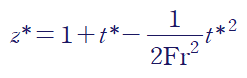
4. 무차원화의 장점
앞선 예제에서는 큰 장점이랄 것이 보이지 않은 것 같습니다.
어차피 같은 결과 아니야? 라고 생각할 수 있지만, 먼저 무차원화가 필요한 이유를 설명하겠습니다.
(1) 앞선 예시는 매우 간단하고 해석적인(analytical solution, exact solution) 해를 구할 수 있는 경우입니다.
(2) 그러나 더 복잡한 상황과 문제가 일반적입니다.(편미분 방정식이나 연립된 미분방정식) 이런 문제들은 손으로 완벽한 해를 구할 수 없기 때문에 공학자들은 수치적으로(numerically)나 실험적으로(experimentally) 문제를 풉니다.
(3) 하지만 비용과 시간이 많이 들기 때문에 방정식을 무차원화하는 것이 매우 유용하고 많은 시간과 비용을 줄여줄 수 있습니다.
어떤 항이 지배적인지, 어떤 항을 무시할 수 있는지 그러한 직관을 제시해준다고 할 수 있겠습니다.
영어 원문 : Relationships between key parameters in the problem are identified. The number of parameters in a nondimensionalized equation is less than the number of parameters in the original equation.
5. 예제2 : 나비에-스톡스 방정식(Navier-stokes equation)
이번 글의 본론이자 하이라이트입니다.
<비압축성 유체>에 대한 나비에-스톡스 방정식입니다.
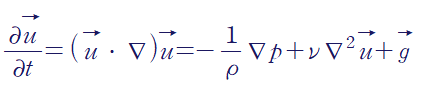
> 무차원 변수를 설정합니다.
(1) 길이(Length)
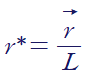
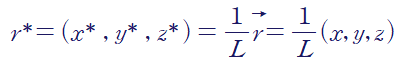
위 정의에 의해 nabla는 아래와 같이 무차원화됩니다.(nabla는 [1/L]의 차원를 가지고 있음)
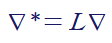
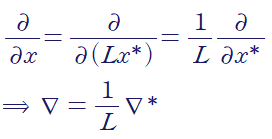
(2) 속도(Flow velocity)
벡터 u를 flow velocity라 하고, U를 특성속도(characteristic velocity)라 합시다. 특성길이나 특성속도같은 것들은 문제에 따라서 사용자가 정의하기 나름입니다.
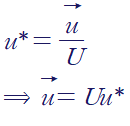
(3) 시간(Time)
앞선 예제1에서와 같이 L/U로 나누어줍니다.
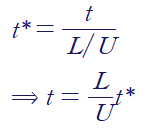
(4) 압력(Pressure)
압력에 대해서는 단일화된 무차원화방식이 없습니다. 여기서는 두 가지 형태로 무차원화하겠습니다.
① 점성 효과가 지배적일 때(viscous effects are dominant)
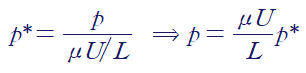
② 관성 효과가 지배적일 때(inertia effects are dominant)
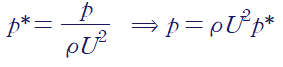
단순하게, 레이놀즈 수(Reynolds number; Re)가 작으면 점성 효과가 지배적, 크면 관성 효과가 지배적이라고 생각합시다.
> 앞서 정의한 관계식을 대입해 방정식을 무차원화합니다.
먼저, 좌변입니다.
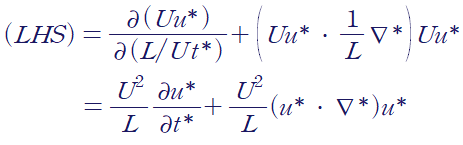
우변의 압력항은 먼저 관성효과가 지배적인 것으로 가정합시다.
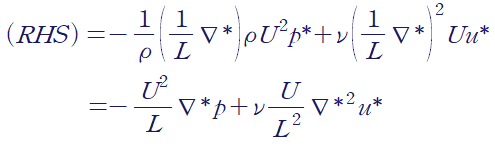
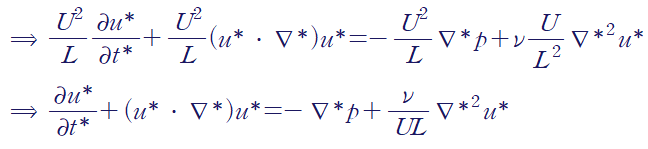
여기서 레이놀즈 수를 다음과 같이 정의하면
무차원화된 나비에 스톡스 방정식(Nondimensionalized NS equation)을 얻을 수 있습니다.
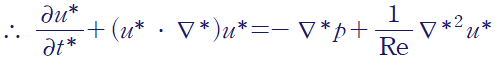
+) 만약 점성효과가 지배적인 상황이라면
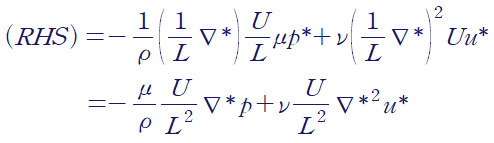
여기서 동점성계수의 정의를 사용합니다.
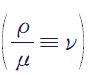
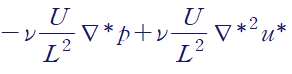
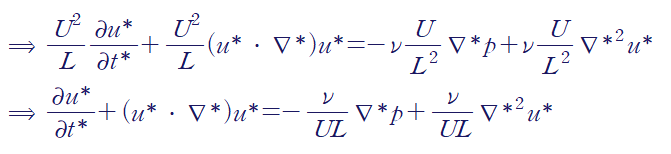
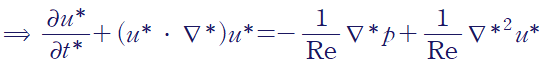
따라서 무차원화된 나비에-스톡스 방정식은 다음과 같습니다.
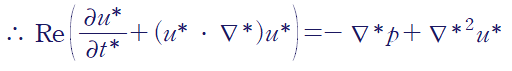
6. 특수한 경우들
앞서 무차원화의 장점에서, 변수간의 관계나 지배적인 효과를 다루기 용이하다고 했습니다.
(1) Stokes regime
Re -> 0 인 경우로 유속이 매우 작아 점성효과가 지배적인 영역입니다.
무차원화된 나비에-스톡스 방정식은 아래와 같이 항이 정리됩니다.
Creeping motion
Stokes equation(diffusion equation)
(2) Euler regime
Re -> ∞ 인 경우로 유속이 매우 크거나 점성항이 매우 작아 관성효과가 지배적인 영역입니다.
점성항을 무시할 수 있으며 아래와 같이 식이 정리됩니다.
레이놀즈 수와 무관한 flow라는 것을 알 수 있습니다.
+)
운동방정식을 무차원화시켜놓고 보니, 무차원변수가 거동에 지배적인 영향을 주고 있다는 것을 볼 수 있습니다. 이 과정을 통해 서로 다른 유체나 다른 길이 스케일에서도 무차원화시킨 데이터들이 같은 경향성을 보인다는 것을 받아들이고 이해할 수 있습니다.
'기계공학 > 4대 역학' 카테고리의 다른 글
| [재료역학] 보의 전단응력 예제(WF보) (0) | 2024.10.21 |
|---|---|
| [유체역학] 개수로 유동(Open Channel Flow) 예제 : Specific Energy (0) | 2024.10.12 |
| [유체역학] 블라시우스 해법(Blasius Solution) 유도 (0) | 2024.06.13 |
| [재료역학] 모어 원 그리는 법(Morh's Circle) (0) | 2024.06.12 |
| [유체역학] 운동량 적분 방정식 유도(Momentum Integral Equation) (1) | 2023.10.06 |