#유체역학

파이프 유동 문제는 관의 형상(지름, 길이), 관의 재질(거칠기, 마찰), 압력 차이가 주된 관심사입니다.
파이프 유동은 internal flow의 대표적인 예이며 유체의 유동을 유발하는 주된 원인이 두 지점의 압력차이가 됩니다.
때문에 내가 A지점에서 B지점까지 유체를 수송하려 할 때 얼마만큼의 압력차이가 요구되는가?라는 것이 설계의 주된 목적이 되며 관의 형상은 유량에 변화를, 관의 재질과 형상은 유동 중 손실되는 에너지에 변화를 줍니다.
때문에 에너지 방정식을 수립하고 상황을 잘 파악해서 식을 잘 정리한다면 어려울 게 없습니다.
파이프 유동에서 가장 복잡한 축에 속하는 문제는 여러 개의 관이 연결된 유동과 난류유동에서 달시 마찰계수 f를 trial and error로 찾는 문제이지만 기본적인 흐름은 동일합니다.
1. Pipe Flow Equations
파이프 유동에서 주로 사용되는 관계식은 다음과 같습니다.
1. 레이놀즈 수의 정의
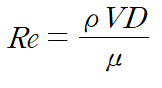
2. 에너지 방정식(V는 평균속도)

3. 수두손실

4. 연속방정식
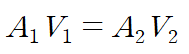
유동이 steady flow라면 Q1 = Q2 이므로 위 관계식이 성립합니다.
5. 관의 단면이 원형이 아닐 경우

거칠기가 주어진다면 동일하게 무디 차트를 읽으면 됩니다.
2. Pipe Flow Examples
파이프 유동 문제는 통상적으로 다음과 같은 메커니즘으로 접근합니다.
1. 층류 / 난류 구분
2. 연속방정식과 에너지 방정식 수립
3. 손실 계산(moody chart)
오늘 풀어볼 문제 순서입니다.
1. 공기의 층류 유동
2. 물의 경사관 유동
3. 여러 개의 관 사이의 유동 결정
4. 사각 덕트의 난류 유동
(예제 1) 공기의 압력이 200 kPa(절대압력)이고 온도가 15도 일 때,
지름이 2.0 cm인 관을 통해 흐르는 최대 층류 유량을 계산하여라
주어진 조건과 목표를 정리합니다.


파이프의 형상이 제시되어있을 때 난류 유동을 유지하며 가질 수 있는 최대 유량을 구하라는 문제입니다.
구해야 하는 유량 Q는 다음과 같습니다.

책마다 다르지만 여기서는 레이놀즈 수가 2100일 때까지를 층류유동이라고 하겠습니다.
레이놀즈 수의 정의를 살펴보면, 모르는 것이 공기의 밀도, 점성계수, 속도입니다.

공기가 이상기체이므로 이상기체 방정식에서 밀도를 얻고 점성계수는 테이블에서 가져오겠습니다.


레이놀즈 수가 2100일 때 최대 속도를 가집니다.

이것을 유량에 대입해 계산하면 문제가 요구하는 최대 유량을 구할 수 있습니다.


(예제 2) 분사 탱크에 부착된 노즐에서 물이 흐르고 있다. 그림에서 보여지는 것처럼 노즐의 손실 계수가 0.75이고 호스의 마찰 계수가 0.11인 경우 유량을 구하여라

출처 : Munson's Fundamentals of Fluid Mechanics
탱크 내부와 대기와의 압력차이로 인해 유동이 발생하는 상황입니다.
이 압력차가 유체의 운동에너지로 변환되며 파이프와 노즐에서 발생하는 손실을 고려해야 하는 문제입니다.
이런 경우 reference를 가장 간단한 지점으로 잡는 게 좋습니다. 분사 탱크의 수면을 1 지점으로 잡으면 주어진 압력 정보와 수면에서 속도가 0이라는 것을 사용할 수 있습니다.

유량을 구해야 하고, 노즐에서의 손실계수를 적용해야 하니 2지점은 당연히 노즐 분사구가 되어야 합니다.
따라서 2지점에서의 압력은 0입니다. (보통 대기압을 0으로 하는 계기압력(gage pressure)을 사용하는데 절대압력을 사용해도 어차피 양변에 같은 수(대기압)가 더해지는 것이므로 같은 결과가 나옵니다.)

수두손실은 주손실과 부손실로 나뉘는데, 관에 의한 주손실(major loss)가loss)이 우변의 첫 번째 항이고 노즐에 의한 부손실(minor loss)이 우변의 두 번째 항입니다.

여기까지 이해한 정보와 상황을 종합하면 다음과 같이 에너지 방정식을 정리할 수 있습니다.

V는 관에서 유체의 평균속도, V2는 노즐에서 사출되는 유체의 평균속도입니다.
관을 지나는 유량과 사출되는 유량이 같습니다.

여기서 노즐의 직경 D2 = 7.5mm, 파이프의 직경 D1 = 15mm 이므로


V2 = 4V입니다.
이쯤에서 모르는 값들을 정리해봅시다.
구해야 하는 유량 Q = AV에서 V를 모르고
정리해 둔 에너지 방정식에서는 V를 제외한 모든 값이 주어져 있으니, 에너지 방정식으로부터 V를 구할 수 있겠군요
연속방정식에서 얻은 V2 = 4V를 대입하고

V제곱의 계수를 깔끔하게 정리하기 위해 양변에 2g를 곱하고

V에 대해 식을 정리하면 다음과 같습니다.

이것을 정리하면 유체의 속도와 유량은 다음과 같습니다.

여기서 V는 파이프 내부에서의 평균속도입니다.
이 문제는 층류인지, 난류인지 확인하는 과정이 없었습니다. 애초에 달지 마찰계수와 손실계수를 모두 주었기 때문에 레이놀즈 수가 필요하지 않았기 때문이기도 하고, 속도 V를 모르는 상황에서 레이놀즈 수를 구하기가 쉽지 않습니다.
만약 마찰계수를 주지 않고 표면거칠기를 주어 무디차트에서 직접 마찰계수를 구해야 했다면 난이도가 더 상승했을 것입니다.
(예제 3) 여러 개의 관 사이의 유동을 결정하는 문제
부손실(minor loss)을 무시할 때, 각 관의 유량을 결정하여라

출처 : Munson's Fundamentals of Fluid Mechanics
왼쪽부터 각 reservoir의 수면을 1,2,3 지점이라 하겠습니다.
문제에서 구해야 하는 것은 각 관의 유량이며, 각 관의 직경이 주어졌으므로 각 관에서의 유체 속도를 구하는 것이 목표가 됩니다.
여러 개의 관 사이의 유동을 결정하는 문제는 "어떤 방향으로 유동하는지"에 대한 가정부터 시작합니다.
먼저 1,2 지점에서 상대적으로 고도가 낮은 3 지점(Elevation = 0)으로 유체가 흐른다고 가정하겠습니다.
흐르는 유량이 보존되어야 한다는(연속방정식) 조건을 사용합니다.

이것에 관의 단면적을 적용하여 정리하면 속도 관계식을 하나 얻습니다.


다음으로는 주손실(Major loss)을 고려한 에너지 관계식을 사용합니다.
1 지점에서 3 지점, 2 지점에서 3 지점으로의 두 가지 관계식을 유도할 수 있습니다.

1 지점에서 3 지점으로 가는 유동은 두 개의 관을 지나니, 두 개의 주손실 항이 발생합니다.
또한 1 지점과 3 지점은 수면이니 P = 0이고 V = 0입니다.
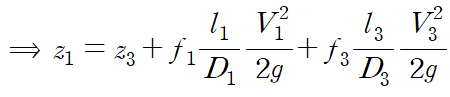
여기서 혼동이 생길 수 있는데, V1, V2, V3는 각각 관을 지나는 속력입니다.
에너지 관계식에서는 편의상 동일한 V를 사용하였지만 그 지점에서의 속력임을 주의합니다.
이를 정리하면 다음과 같습니다.


마찬가지로 2 지점과 3 지점 사이의 유동에 에너지 관계식을 적용합니다.

세 번째 관계식을 얻습니다.
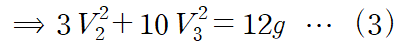
지금까지 얻은 관계식을 종합해 보면 다음과 같습니다.

그러나 이 연립방정식의 해는 존재하지 않습니다.
따라서 처음에 1,2 => 3로 흐른다는 가정이 틀렸으며, 다음으로 해볼 수 있는 "합리적인" 가정은 2 => 1,3으로 흐른다는 것입니다.
앞선 과정을 다시 수행합니다.


이것을 연립하여 각 관에서 유체의 속도를 구할 수 있습니다.
변수가 여러 개인 이차 연립방정식은 상수항이 없는 두 문자에 대한 이차식을 얻는 것으로 해를 구할 수 있습니다.
V1과 V2로 정리합니다.




이 이차방정식을 V1에 대하여 풀면 V1 = 1.002 V3이라는 관계를 얻습니다.

이것을 원래 가지고 있던 식에 대입해 모두 정리하면 ((4)식에 대입)


위와 같이 속도를 구할 수 있으며
이를 이용해 각 관에서의 유량 Q1, Q2, Q3을 구할 수 있습니다.

(예제 4) 표면의 거칠기가 ε = 0.015mm 인 직사각형 덕트에 공기가 0.068 m^3/s의 유량으로 유동중일 때 이 12m 덕트에서 발생하는 수두손실을 구하여라.
덕트의 사이즈는 0.15m x 0.30m이다.

그림과 같은 사각 덕트에서 공기가 유동 중이며 발생하는 수두손실은 표면의 거칠기로 인한 주손실(Major loss)만 고려합니다.

그러나 위 식은 포아실리 법칙을 통한 원형관의 수두손실입니다.
단면이 비원형인 경우 수력직경(hydraulic diameter)을 사용해 레이놀즈 수와 손실계수를 정의합니다.


A는 단면적, P(Perimeter)는 단면의 둘레입니다.
이제 마찰계수 f만 구하면 되는데 f가 주어져있지 않기 때문에 먼저 층류인지, 난류인지 확인해야 합니다.
층류인 경우 f = 64/Re 식을 사용하고 난류인 경우 무디 차트를 읽어야 합니다.
레이놀즈 수를 구합니다.

저는 간편하게 동점성계수로 바꿔서 한 번에 계산했습니다.
유량과 단면적이 주어졌으니 속도를 구하고

레이놀즈 수를 구합니다(동점성계수 1.4 x 10^-5 사용)

레이놀즈 수가 난류의 기준인 4000을 넘으니 공기의 유동이 난류 유동임을 알 수 있습니다.
따라서 무디 차트를 읽어 마찰계수를 구해야 합니다.(거칠기가 주어진 것에서 무디 차트를 예측할 수 있습니다)
레이놀즈 수를 알고 있으니 상대거칠기를 구하고 무디 차트를 읽습니다.


f가 대략 0.026 임을 알 수 있습니다.
따라서 사각 덕트 12m를 지날 때 발생하는 수두손실은 다음과 같습니다.

'기계공학 > 4대 역학' 카테고리의 다른 글
| [유체역학] 수력도약(Hydraulic Jump) (1) | 2023.08.05 |
|---|---|
| [재료과학] 재휘현상(Recalescence) (0) | 2023.06.30 |
| [열역학] 맥스웰 관계식, 열역학 관계식 예제 (0) | 2023.04.03 |
| [유체역학] 달시 마찰 계수, 무디 차트 보는 법 (0) | 2023.03.31 |
| [열역학] 맥스웰 관계식 (Maxwell Relations) (0) | 2023.03.10 |