#유체역학
0. Introduction
수력도약 현상(Hydraulic Jump)은 빠른 속도로 흐르는 유체가 갑자기 솟아오르는 듯한 현상으로, 수도꼭지에서 물을 세게 틀면 물줄기가 거세지며 두꺼워지는 것이 바로 이 수력도약 현상의 일종입니다.

다른 대표적인 예로는 계곡물이 어느지점에서 두꺼워지는 현상입니다


수력도약 현상이 정확히 "왜" 일어나는지에 대한 원인은 불분명합니다. 어떤 임계속도를 넘어선 빠른 유동에서 작은 턱(언덕같은, 방지턱 같이 생각)을 만날 때 주로 발생합니다. 하지만 유동의 폭이 늘어났기 때문에 유속은 감소해야만 하고 수력도약 현상이 일어나는 초기 지점에서 소용돌이(vortices)가 발생하며 많은 에너지 손실이 발생한다는 문제점도 있습니다.
이 게시글에서는 수력도약 관계식을 유도하고 예제를 풀어보겠습니다.
1. Hydraulic Jump
아래 관계식은 수력도약 전의 유동 깊이(y1)와 이후의 유동 깊이(y2)의 관계식을 나타낸 식입니다.(Fr : Froud number)
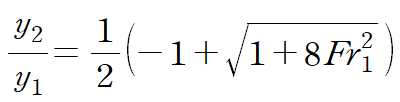
수력도약을 위해서는 유체가 얼마만큼의 속력을 가져야 하며 수력도약 현상 이후 유동 깊이(flow depth)은 어떻게 변화하는지 수학적으로 유도해봅시다.
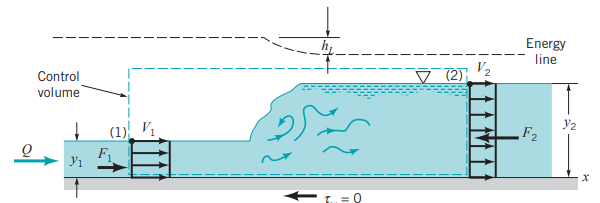
아래와 같이 검사체적을 설정하고 해석적인 해를 구하기 이전에 다음과 같은 가정이 요구됩니다.
1. 정상상태(Steady State) 유동이다
2. (1)지점과 (2)지점을 지나는 속도는 V1, V2로 일정하다
3. 벽면에 작용하는 전단응력(wall shear stress)을 비롯한 모든 에너지 손실을 무시한다
4. 유동시 가로폭(width)이 일정하다
세 가지 방정식이 사용됩니다.
(1) 연속 방정식(Continuity Equation)
(2) x방향 검사체적 운동량 방정식(Momentum Equation)
(3) 에너지 방정식(Energy Equation) : 이는 베르누이 방정식과 유사합니다.
(1) 에너지 방정식
정상상태 유동이기 때문에 (1)지점에서의 유량와 (2)지점에서의 유량이 같습니다.
가로폭을 b라고 한다면 다음과 같은 관계식을 얻을 수 있습니다.
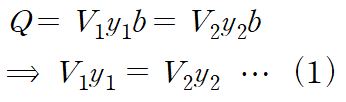
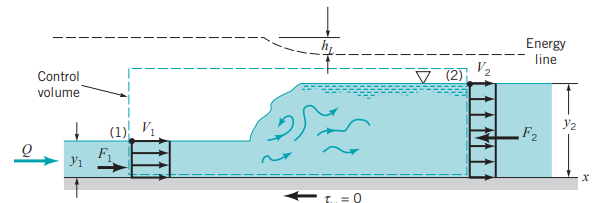
(2) x방향 운동량 방정식
검사체적의 표면에 발생하는 힘은 (1)지점에 발생하는 F1과 (2)지점에 발생하는 F2가 있습니다.
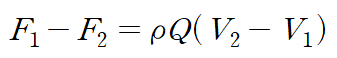
이 두 힘은 모두 정수력에 해당하며 다음과 같이 기술됩니다.
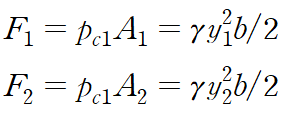
이것을 대입합니다.
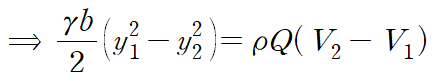
비중량의 정의와 앞서 구한 연속방정식을 대입합니다.
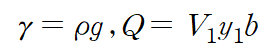
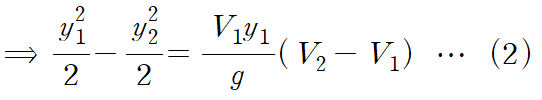
(3) 에너지 방정식
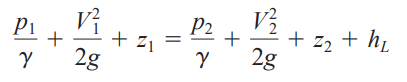
위와 같은 에너지 방정식을 적용할 건데 지금 살펴보고 있는 개수로 유동 문제(Open Channel Flow)의 경우
다음과 같이 에너지 방정식이 정리됩니다.
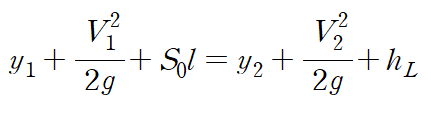
S0는 개수로의 기울기를, hL은 에너지 손실수두(head loss)를 의미합니다.
이 문제에서는 기울기가 0이고 에너지 손실을 무시한다고 하였으니 S0 = hL = 0입니다.
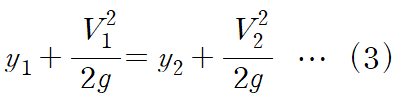
이제 (1), (2), (3) 세 개의 관계식을 연립합니다.
먼저 운동량 방정식으로부터 얻은 (2)에 연속방정식(1)을 적용합니다.
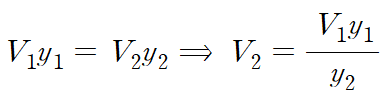
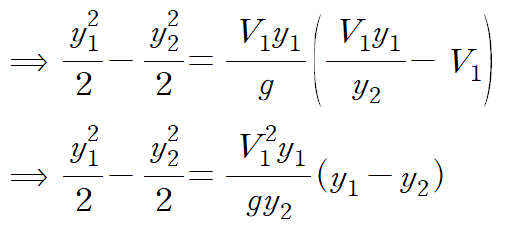
이때 좌변이 다음과 같이 인수분해가 됩니다.
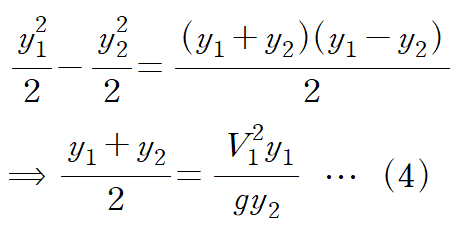
이때 프루드 수(Froud Number; Fr)의 정의와 유사한 형태가 우변에 있습니다.
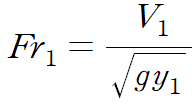
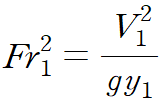
이것을 (4) 식에 대입합니다.
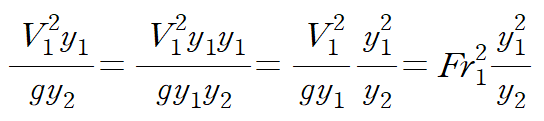
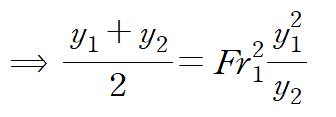
양변을 y1^2/y2 로 나누어 정리하면 다음과 같은 이차식을 얻습니다.
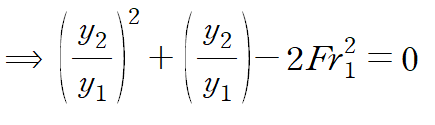
마지막으로 y2/y1 에 대한 이차방정식으로 보고 근의 공식을 사용해 해를 구하면 다음과 같습니다.
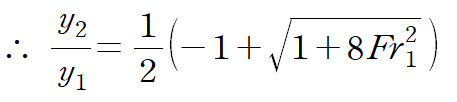
수력도약이 일어나기 위해서는 우변이 1보다 커야겠죠? 그래야 수력도약 이후의 유동깊이(y2)가 y1보다 커질 테니까요
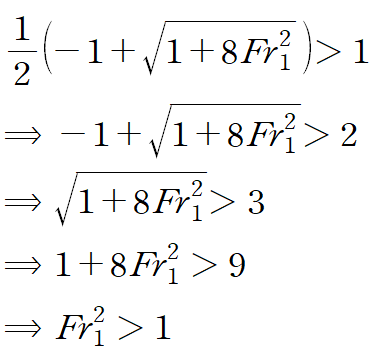
이것이 의미하는 것은 수력도약이 일어나기 위해서는 프루드 수(Fr)가 1보다는 커야한다는 것을 의미합니다.
여기서 프루드 수가 1보다 크다고 무조건 수력도약이 일어나는 것은 아닙니다!
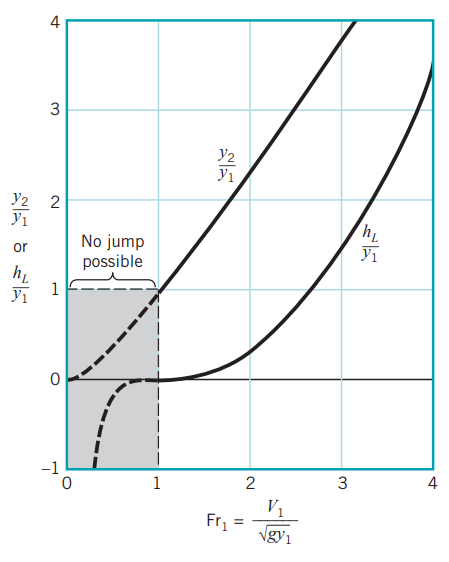
Froud number에 따른 수력도약 현상은 다음과 같습니다.
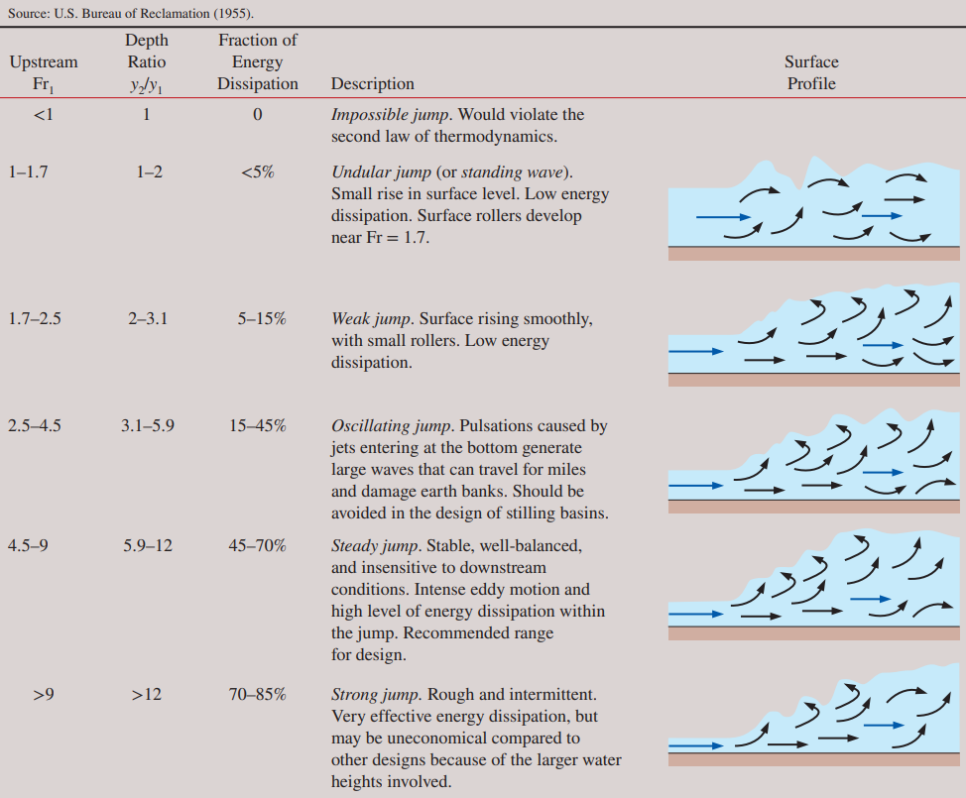
2. Example
(예제) 상류의 유동 깊이가 0.3m, 하류의 유동 깊이가 1.2m 일 때, 상류에서의 유속을 구하여라

photo by BRINGHAM YOUNG UNIVERSITY
수력도약 관계식을 사용합니다.
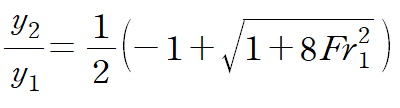
구해야 하는 것은 상류(y1 = 0.3m인 지점)에서의 유속 V1입니다.
이것은 위 관계식에서 우변에 위치한 Fr1과 관계가 있습니다.
먼저 y2/y1 = 1.2/0.3 = 4 이므로 이것을 대입합니다.
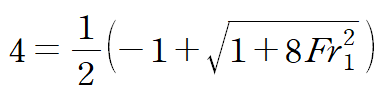
양변을 정리하여 프루드 수를 구할 수 있습니다.
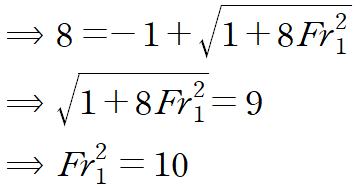
프루드 수의 정의를 사용해 유속을 구합니다.
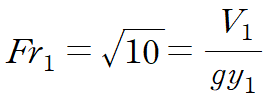
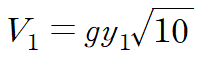
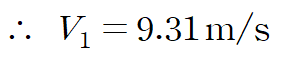
'기계공학 > 4대 역학' 카테고리의 다른 글
| [유체역학] 운동량 적분 방정식 유도(Momentum Integral Equation) (1) | 2023.10.06 |
|---|---|
| [유체역학] 항력계수(Drag Coefficient) (0) | 2023.08.09 |
| [재료과학] 재휘현상(Recalescence) (0) | 2023.06.30 |
| [유체역학] 파이프 유동 예제 : 에너지 법칙, 수두손실 (0) | 2023.04.19 |
| [열역학] 맥스웰 관계식, 열역학 관계식 예제 (0) | 2023.04.03 |