[공업수학] 2.2-1 상수계수를 가지는 제차 선형 상미분 방정식 (Homogeneous Linear ODEs with Constant Coeffici
공업수학(상)(Kreyszig)(Kreyszig)(10판) 『Kreyszig 공업수학, 10판』 상권. 이 책은 반세기 동안 전 세계적으로 가장 널리, 그리고 가장 많이 채택되어 사용되고 있는 Erwin Kreyszig 교수가 저술한 Advanced Engi
subprofessor.tistory.com
#공업수학
제차 ODE가 거의 다 끝나갑니다. 이번 시간에 오일러-코시 방정식을 배우고 나면 사실상 2계 제차 ODE는 더 배울 것이 없습니다. Wronskian은 두 해가 basis인지 확인할 수 있는 Tool인 동시에 비제차 방정식의 해를 구하는 데 도움이 되는 Tool이라 2계 제차 ODE의 핵심적인 내용은 이번 포스팅이 마지막이 되겠네요
1. Euler-Cauchy Equation
다음과 같은 형태의 ODE를 오일러-코시 방정식(Euler-Cauchy Equation)이라 합니다
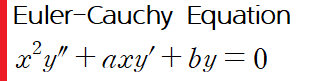
이런 형태의 미분 방정식은 해를 다항함수라고 가정하고 접근해야 합니다. 다항함수를 미분하면 차수가 1 감소하니, 주어진 미분방정식의 모든 항의 차수가 같게 됩니다. 아래와 같이 설정해주고 진행해볼게요
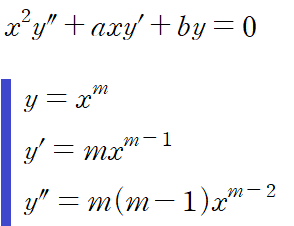
y, y', y''를 오일러-코시 방정식에 대입하면
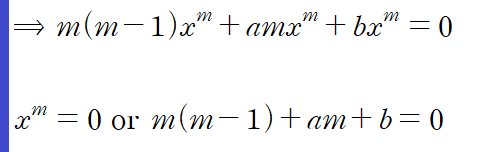
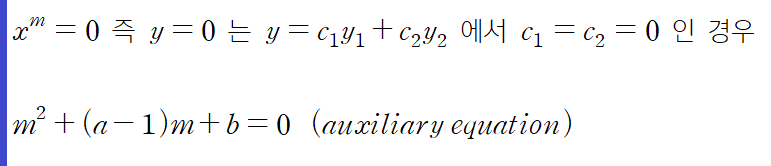
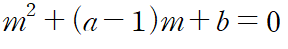
위 식을 보조방정식(auxiliary equation)이라고 부르는데, 2.2에서 나온 특성방정식(characteristic equation)과 같은 느낌입니다. 상수계수 미분방정식의 경우 자연로그를 밑으로 하는 지수함수의 지수를 결정했다면, 오일러-코시 방정식의 경우 다항함수 x^m의 차수 m을 결정합니다. 둘 다 같은 용도인데 왜 다르게 불리는지는 잘 모르겠어요. 원서에도 따로 나와있는 내용이 없습니다
<CASE I>
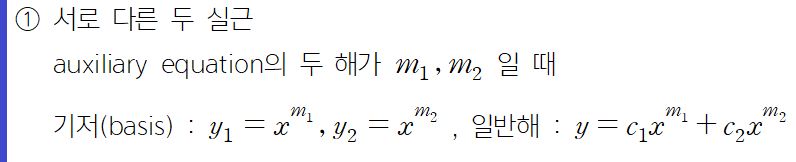
<CASE II>

두 번째 기저는 상수계수 미분방정식과 마찬가지로 Reduction of Order를 이용해서 구할 수 있습니다

보조방정식(auxiliary equation)의 해는 중근의 경우 m=-(a-1)/2 가 나옵니다 (직접 해를 구해봅시다)

<CASE III>
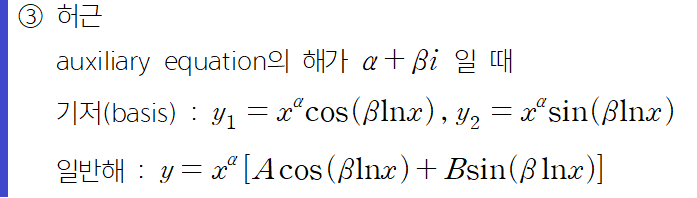
기저의 형태가 특이하지요? 상수계수 미분방정식의 특성방정식이 허근일 경우 삼각함수 꼴로 유도되는 과정과 비슷합니다

이 부분이 조금 난해하게 느껴질 수 있는데, 정상입니다. x=e^lnx 로 바꾸어 생각한다는 발상 자체가 익숙치 않기 때문에 처음 보시는 분들은 몇 번 반복학습을 통해 익히시길 바랍니다
2. 예제
(예제 1) 다음 미분방정식의 해를 구하여라


(예제 2) 다음 미분방정식의 해를 구하여라
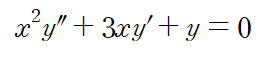
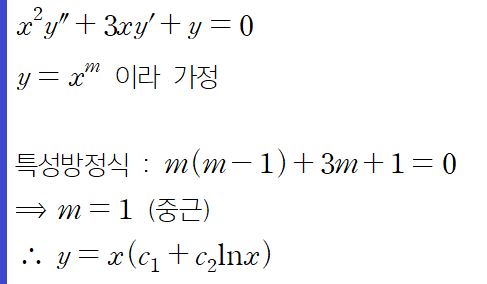
(예제 3) 다음 미분방정식의 해를 구하여라

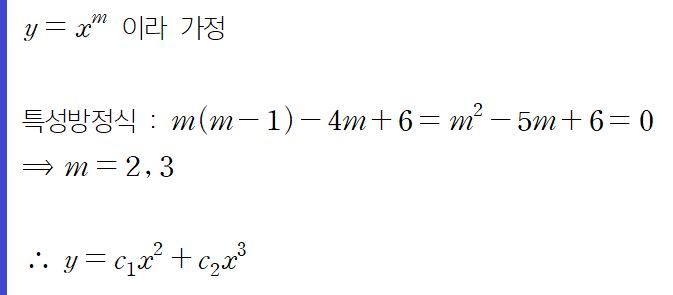

(예제 4) 다음 미분방정식의 해를 구하여라
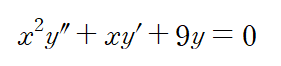
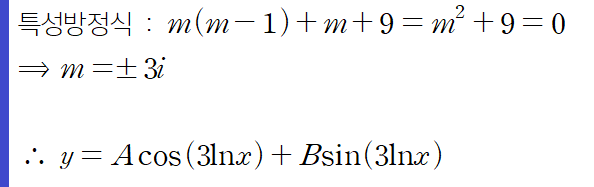
허수부가 삼각함수 안에 있는 lnx의 계수가 된다는 사실을 기억하시면 됩니다
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 2.7-1 2계 비제차 미분방정식 : 미정계수법(Method of Undetermined Coefficients) (1) | 2023.01.21 |
|---|---|
| [공업수학] 2.6 론스키 행렬식(Wronskian) (0) | 2023.01.11 |
| [공업수학] 편미분 방정식 (3) : 비제차 방정식(Time-dependent) (0) | 2023.01.07 |
| [공업수학] 2.2-2 상수계수를 가지는 제차 선형 상미분 방정식 예제 (0) | 2023.01.07 |
| [공업수학] 2.2-1 상수계수를 가지는 제차 선형 상미분 방정식 (Homogeneous Linear ODEs with Constant Coefficients) (0) | 2023.01.07 |