[공업수학] 2.6 론스키 행렬식(Wronskian)

 

#공업수학

 

 

Wronskian(론스키안?)은 함수와 함수간의 선형독립성(Linear Independence)을 판단하는 도구입니다. 혹 왜 선형독립성을 따져야 하냐는 질문을 한다면.. 너무 절망스러울 것 같습니다.. 여기까지 왔는데 그런 질문을 하시면 정말.. 그런 분들을 위해서 위에 링크를 준비해 두었습니다. 관련포스팅 아래 2.1-2 배너를 들어가보시면 왜 선형독립성을 판단할 수 있어야 하는지 알 수 있습니다. 간단히 말하자면 2계 이상의 미분방정식은 선형독립인 해들의 선형결합으로 일반해가 표현되기 때문입니다.

​

Wronskian은 이 개념을 처음 도입한 수학자 Józef Maria Hoene-Wroński 가 본인의 이름을 따서 붙인 이름인데 궁극적으로는 Wronski 행렬식을 의미합니다.

​

 

y1, y2, ··· , yn 의 Wronski 행렬식

 

​

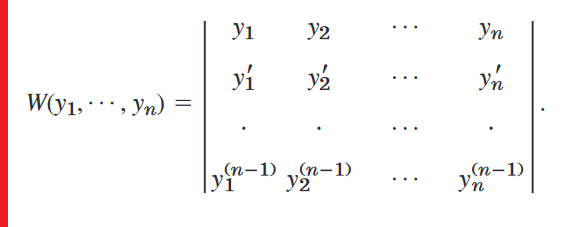
행렬식 계산방법을 여기서 다루지는 않겠습니다. 선형대수학을 제대로 이수하셨다면 큰 어려움은 없을 테지만 까먹으신 분들을 위해 관련 링크를 남깁니다.

​

 

https://ratsgo.github.io/linear%20algebra/2017/05/21/determinants/

행렬식(determinant) · ratsgo's blog

 

 

 

​

2계 미분방정식의 Wronskian을 먼저 보기보다는 Wronskian의 정의를 먼저 보고 그 다음 2계 미분방정식의 경우를 보는 순서를 밟도록 합시다.

 

 

Wronskian 의 정의

 

 

​

​

 

Wronskian을 이용한 선형독립성 판별

 

 

2계 이상의 제차 선형 미분방정식의 일반해는 선형독립인 기저들의 선형결합으로 나타낼 수 있습니다. 이게 서로 선형독립인지 종속인지 판별하기 어려운 경우, Wronskian을 이용해주면 됩니다. 간단하게 Wronski 행렬식이 0이 아니면 선형독립입니다

​

​

 

반응형

​

​

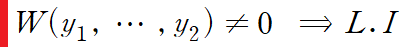
예시를 봅시다

​

선형독립성은 "집합"의 성질입니다. 벡터들이 모인 집합의 성질이 될 수도 있고 함수들이 모인 집합의 성질이 될 수도 있습니다. Wronski 행렬식을 이용해 선형독립성을 판별해봅시다

​

​

​

​

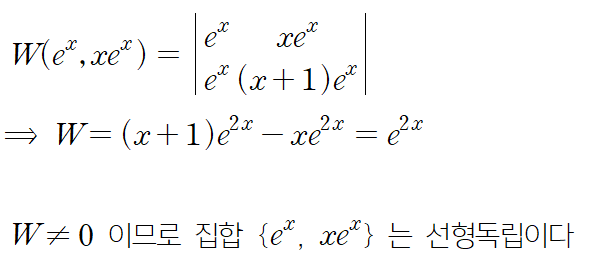
이런 느낌으로 Wronskian을 사용해주시면 됩니다. 나중에 비제차(nonhomogeneous) 방정식의 해를 구할 때 다시 나오니 필히 기억하시길 :)