이번시간에는 2계 미분방정식의 IVP와 General Solution을 이루는 Basis들에 대해 알아봅시다
(i) 2계 미분방정식의 IVP
IVP는 Initial Value Problem의 약자입니다. 1계일 경우는 아래와 같은 형태로 초깃값이 주어졌는데, 2계 이상의 경우에는 그 도함수들의 초깃값이 주어집니다

2계 미분방정식의 IVP는 아래와 같은 초깃값이 주어집니다
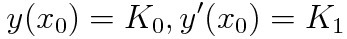
이게 끝입니다. 왜 y의 다른 함숫값을 주어주면 안 되지?라는 질문이 떠오를 수도 있는데 아주 좋은 질문입니다. 우리가 애초에 IVP, 초깃값 문제라고 부르는 것들은 초기물리량을 측정하기가 용이하기 때문이었으니, 변화량의 초기물리량 또한 측정하기가 비교적 수월하기 때문이라고 이해하면 되겠습니다. 지난 시간에 중첩원리를 공부하며 예시로 나온 y''+y=0을 IVP 예제로 풀어봅시다
(예제 1) 다음 미분방정식의 해를 구하여라

일반해가 아래형태였다는 것 기억하시죠?

여기에 초기조건을 적용해주면
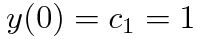

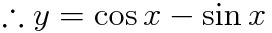
과 같은 특수해(particular solution)를 얻을 수 있습니다
(ii) Basis (기저), General Solution(일반해)
Basis는 선형대수학을 공부한 학생들에게는 조금 익숙한 용어일 텐데요 한국어로는 기저로 번역되는 이 Basis는 대체 무엇인지, 이 Basis가 되기 위한 조건은 무엇인지 알아봅시다
① Basis란 무엇인가?
선형대수학에서는 Vector들의 집합을 뜻하고, 미분방정식에서는 일반해를 표현하기 위한 함수들. 정도로 이해하면 됩니다. 저번에 배운 중첩원리에 따르면 2계 이상의 제차방정식에서는 무수히 많은 해들이 존재하는데, 그 무수히 많은 해 들을 효율적으로 그리고 체계적으로 표현하기 위한 방법이라고 이해하시면 됩니다. 저번 시간에 2계 미분방정식의 예제로 든 y''+y=0의 해가 cos x, sinx의 무수한 선형결합이었던 것처럼 2계 이상의 제차방정식의 해는 basis들의 선형결합으로 표현합니다

② Basis가 되기 위한 조건
먼저 교재에서 말하는 Basis의 정의를 보자

여기서 말하는 (2)는 아래 2계 제차방정식을 말합니다

정의를 한국말로 풀어서 설명하면, 선형독립(linearly indepent)인 Solution들의 집합을 basis라고 한다는 것입니다.
선형독립은 일차독립이라고도 불리는데, 반대의 개념이 되는 선형종속을 이해하면 선형독립의 이해가 쉬워집니다.

즉, 어떤 해가 다른 해의 상수배 꼴로 표현되면 두 해는 선형종속입니다
위에서 초깃값문제의 예제로 든 y''+y=0의 경우를 한번 더 봅시다

cos x는 어떤 상수를 곱하더라도 sin x가 될 수 없죠? 따라서 cos x와 sin x는 선형독립입니다.
(예제 2) 다음 미분방정식의 기저와 일반해를 구하여라
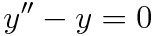
해를 어떻게 구하는지는 나중에 배우고, 일단 직관적으로 해를 구해봅시다
두 번 미분해서 자기 자신이 나오는 함수.. 를 생각해보면 아래 두 함수가 바로 떠오르죠?


대입해서 확인해보아도 해가 됨을 알 수 있죠(실제로 해보시길 추천)
두 함수는 서로 상수배로 나타낼 수 없기 때문에 Basis로서의 조건을 충족합니다
따라서 주어진 미분방정식의 일반해를 Basis로 나타내면 다음과 같습니다.

'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 2.2-1 상수계수를 가지는 제차 선형 상미분 방정식 (Homogeneous Linear ODEs with Constant Coefficients) (0) | 2023.01.07 |
|---|---|
| [공업수학] 2.1-3 계수내림 (2) | 2023.01.06 |
| [공업수학] 편미분 방정식 (2) : 비제차 방정식(Time-Independent) (0) | 2023.01.04 |
| [공업수학] 2.1-1 중첩원리 (Superposition Principle) (2) | 2023.01.04 |
| [공업수학] Homogeneous Linear ODEs of Second Order에서 중첩원리 증명 (0) | 2023.01.04 |