지금까지는 1계 미분방정식 즉 y'가 들어간 미분방정식의 해를 구해보았다면, 이제 y''가 들어간 2계 미분방정식을 다루어봅시다. 2계 미분방정식의 활용도는 정말 높아서(F=ma라던지) 공대생이라면 필수적으로 알아야 하는 파트입니다. 그 기반이 되는 "2.1 Homogeneous Linear ODEs of Second Order"는 양 자체가 거대하기도 하고 나중에도 쓰이는 Basic Material이 많기 때문에 세 파트로 나눠서 포스팅 합니다.

(i) 2계 선형방정식의 형태
2계 선형 상미분방정식(Linear ODEs of Second Order)의 형태는 다음과 같습니다.

기본적인 형태는 1계 선형방정식과 크게 다름이 없죠?


이런 애들을 2계 선형 상미분 방정식이라고 분류합니다.
2.1에서는 2계 선형 상미분방정식 중 r(x)=0인 형태 즉 제차방정식을 다루는데요,
이번 포스팅에서는 선형 제차방정식들의 특성 중 중첩원리(Superposition Principle)에 대해서 알아봅시다.

(ii) 중첩원리
정의를 확인하기 전에 먼저 예시부터 살펴보고 갑시다.

위 미분방정식의 해를 찾아봅시다.

이렇게 놓으니까 두 번 미분해서 자기 자신에다가 마이너스를 곱한 것이 나오는 함수...를 의미하는 미분방정식이네요
그런 함수가 뭐가 있을까 생각해보니 삼각함수 cos x와 sin x가 생각나네요.


조건을 만족하는군요. 따라서 cos x와 sin x는 주어진 미분방정식의 해입니다. 그런데 자세히 보니까 이 둘을 합한 것도 해가 됩니다

그렇다면 cos x의 상수배는 어떨까요? 그렇습니다. 그것 또한 주어진 미분방정식의 해가 됩니다.

●
●
●
2계 선형방정식의 중첩원리의 정의는 다음과 같습니다.

여기서 선형결합(linear combination)이라는 용어는 선형대수학에서도 나오는 그 용어가 맞습니다.
linear combination에 대한 추가적인 정보가 필요한 분은 아래 링크를 이용해주세요
https://junklee.tistory.com/75
선형결합
학습목표 이번 강의에서는 벡터들 간의 선형결합에 대한 개념과 벡터공간 상의 Span의 개념에 대해 알아보겠습니다. 그리고 선형결합과 관련하여 네 가지의 새로운 관점을 통해 행렬의 곱셈을
junklee.tistory.com
중첩원리에 따르면,
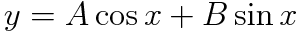
여기서 주의해야 할 것은 "제차방정식에 대해서만 성립한다는 점!"
비제차방정식에 대해서는 성립하지 않습니다.
중첩원리는 후에 Basis와도 연결되는 개념이고 Higher Order ODE(3계 이상의 미분방정식)에서도 나오니 꼭 한번쯤 증명해보고 넘어가길 권장드립니다. 증명과정이 그렇게 복잡한 것도, 어려운 개념을 요망하는 것도 아니기 때문에 귀찮더라도 5분, 10분만 투자하시고 기반을 잘 쌓으시길 바랍니다. 다음 포스팅은 2계 미분방정식에서의 초깃값문제는 어떻게 주어지는지에 대해서, Basis와 Supoerpostion Principle을 통한 일반해의 형태에 대한 내용입니다.
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 2.1-2 IVP(2계 미분방정식의 초깃값 문제), Basis, General Solution(일반해) (0) | 2023.01.05 |
|---|---|
| [공업수학] 편미분 방정식 (2) : 비제차 방정식(Time-Independent) (0) | 2023.01.04 |
| [공업수학] Homogeneous Linear ODEs of Second Order에서 중첩원리 증명 (0) | 2023.01.04 |
| [공업수학] 1.5-2 베르누이 방정식(Bernoulli Equation) (3) | 2023.01.02 |
| [공업수학] 연립미분방정식 예제 : 비제차 방정식 (Nonhomogeneous Equation) (0) | 2023.01.01 |