#공업수학
제차 편미분 방정식의 소개와 푸리에 변환을 활용한 풀이는 아래 게시글 참조 바랍니다
1. Types of Nonhomogeneous PDEs
비제차 방정식은 독립변수로 이루어진 항 또는 종속변수 항이 존재하는 미분 방정식입니다.
아래 편미분 방정식을 예시로 들어볼 수 있겠죠

여기서 한 가지 분류가 더 등장하는데 바로 시간과 연관이 있느냐입니다.
비제차 항과 경계조건을 기준으로 시간 t가 연관이 있으면 time - dependent PDE
시간 t와 연관이 없으면 time - independent PDE입니다.
위에서 예시로 든 PDE (1)은 비제차 항에 t가 포함되어 있으므로 time - dependent PDE 입니다.
비제차 편미분 방정식은 시간과 연관이 있느냐에 따라서 풀이의 방향이 완전히 다르기 때문에 비제차 항과 경계조건을 꼭 유심히 살펴보아야 합니다. 예시를 더 살펴보겠습니다.


PDE(2)는 비제차 항과 경계조건 모두 시간과 연관이 없는 time - independent PDE이고
PDE(3) 은 비제차 항에는 t가 없지만 경계조건이 시간의 영향을 받는 time - dependent PDE입니다.
2. Time - Independent PDEs
시간과 연관이 없는 비제차 방정식의 경우 다음과 같은 방법으로 해를 구합니다.

※ ψ 는 psi (프사이)라고 읽습니다
상미분 방정식의 경우에는 제차해와 비제차해를 각각 따로 구했는데 편미분 방정식의 경우 아예 처음부터 해를 두 개로 가정합니다.
다음과 같은 heat equation을 예시로 들어보겠습니다.

(i) 종속변수 u(x, t)를 두 함수의 합으로 분리(가정)합니다.

(ii) 이것을 PDE에 적용하여 두 개의 방정식으로 분리합니다.

위 식에서 x로만 이루어진 항들의 합이 0이라고 가정한다면 다음과 같이 두 개의 식으로 분리할 수 있습니다.


이때 주의할 것이 있습니다. 경계조건은 모두 ψ(x)가 가져간다고 설정합니다.

즉 분해되어 정리되는 두 방정식은 다음과 같습니다.


※u의 초기조건으로부터 v의 초기조건을 구할 수 있습니다.

※ 개인적으로는 우리가 익숙한 제차 PDE의 형태로 만들기 위한 거라고 이해하는 게 편하다고 생각합니다.
(iii) 각각의 방정식을 풀고 u로 합칩니다.

첫 번째 방정식의 해는 다음과 같습니다. 구하는 방법은 제차 PDE를 풀 때와 동일하므로 생략하겠습니다.

꼭 손으로 직접 해를 구해보시고 왜 위와 같은 해가 나오는지 모르겠다면 아래 글 참조 바랍니다.
계수 An은 초기조건을 이용해 구할 수 있는데 ψ를 알아야 하므로 통상적으로는 두 번째 방정식의 해를 먼저 구합니다.

단순히 양변을 x에 대해 두 번 적분하고, 나오게 되는 두 개의 적분상수를 경계조건으로 처리해주면 됩니다.


An을 구하면 v(x, t)가 구해지니

이상의 결과들을 정리해 u(x, t)를 구할 수 있습니다.
풀이가 너무 길고 복잡하니 예제를 하나 더 보겠습니다.
(예제) Solve the boundary-value problem

비제차 항과 경계조건이 시간과 무관하므로 time - independent PDE입니다. 그러므로
(i) ψ(x)를 도입해 u를 분해합니다.

(ii) PDE에 대입하여 두 개의 방정식으로 분리합니다.

★ 경계조건이 모두 ψ 로 가야 합니다.


(iii) 먼저 방정식 (1)을 풀어 ψ 를 구하고 그 결과를 통해 v를 구합니다

이때 해를 지수함수로 표현할 수도 있지만 경계조건 ψ(0)=0을 유용하게 사용하기 위해 쌍곡선 함수를 사용합니다.(지수함수를 사용해서 풀어도 같은 해가 나오지만 쌍곡선 함수를 사용하면 더 간단합니다)
쌍곡선 함수에 대한 정의와 성질은 아래 링크 참조 바랍니다.
https://ko.wikipedia.org/wiki/%EC%8C%8D%EA%B3%A1%EC%84%A0_%ED%95%A8%EC%88%98
쌍곡선 함수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 수학에서 쌍곡선 함수(双曲線函數, 영어: hyperbolic function)는 일반적인 삼각함수와 유사한 성질을 갖는 함수로 삼각함수가 단위원 그래프를 매개변수로 표시할
ko.wikipedia.org
경계조건을 적용하여 c1, c2를 처리합니다.


이제 두 번째 방정식의 해를 구합니다.
변수분리 가정을 사용해 v(x, t) = X(x) T(t)로 상정합니다.

양변을 XT로 나누고

더 높은 미분항을 가진 X가 간단해지도록 식을 정리하고 λ을 도입해 각각에 문자 x, t에 대해 방정식을 분리합니다.

X(x) 먼저 구하면

이때 경계조건을 만족하는 λ는 양수만 가능합니다.

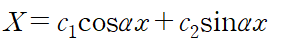
경계조건을 적용합니다.



다음으로는 T(t)를 구합니다.


이때 λ = α^2 = n^2 이므로

따라서 v(x, t)는 다음과 같습니다.

c2를 결정하기 위해 초기조건을 적용합니다.
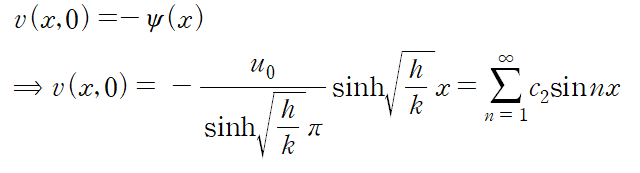
c2는 푸리에 사인 급수의 계수이므로 다음과 같습니다.

피적분 함수가 쌍곡선함수와 삼각함수의 곱이므로 부분적분을 이용해 간단히 할 수 있습니다.





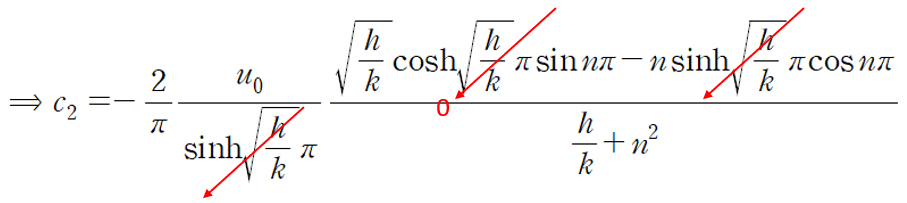
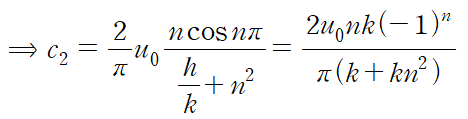
이상의 결과들을 통해 해를 정리하면 다음과 같습니다.


time - independent PDE의 풀이를 다시 정리해 보겠습니다.
- u(x,t) = v(x,t)+Ψ(x)로 분해. 이 때 경계조건은 모두 Ψ에 할당
- PDE에 대입 후 두 개의 방정식으로 분리
- 각각의 방정식의 해를 구하기
- Ψ(x)를 먼저 구함
- v(x, t)는 변수분리로 해를 구하는데 경계조건이 모두 0 이므로 X(x)는 삼각함수만 해로 가질 수 있다. (만약 경계조건이 도함수로 제시된다면 n = 0인 상수 해도 고려해야 합니다)
- v(x, t)에서 급수 내부의 계수는 초기조건을 사용하여 구한다
4. 마지막으로 u(x, t)로 정리하기
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 2.1-3 계수내림 (2) | 2023.01.06 |
|---|---|
| [공업수학] 2.1-2 IVP(2계 미분방정식의 초깃값 문제), Basis, General Solution(일반해) (0) | 2023.01.05 |
| [공업수학] 2.1-1 중첩원리 (Superposition Principle) (2) | 2023.01.04 |
| [공업수학] Homogeneous Linear ODEs of Second Order에서 중첩원리 증명 (0) | 2023.01.04 |
| [공업수학] 1.5-2 베르누이 방정식(Bernoulli Equation) (3) | 2023.01.02 |