이번시간에는 베르누이 방정식에 대해서 알아봅시다. 이 베르누이 방정식이라는 특별한 형태의 미분방정식을 아는 것도 중요하지만 "치환"을 해서 선형방정식을 유도하는 과정을 익히는 것이 더 중요합니다.
(i) 베르누이 방정식

위 형태의 방정식을 우리는 1계 선형 상미분 방정식 이라고 분류했었고, 어떻게 푸는지도 1.5-1에서 공부했습니다.

그렇다면 우변이 위와 같은 형태로 되어있을 때는 어떻게 해야 할까요? 우변의 a가 0 또는 1인 경우에는 1.5-1에서 배운 1계 선형 상미분 방정식 푸는 방법으로 풀면 되는데, 그렇지 않은 경우에는 비선형방정식(nonliear equation) 이 됩니다. 이런 방정식은 어떻게 풀 수 있을까요?
결론부터 말하자면

이놈을 이용합니다.

(a)식의 양변을 x에 대해 미분합시다.


베르누이 방정식의 형태를 조금 손봐주고 (b)식에 대입합니다.

잘 정리해주면 (d)를 얻습니다


이므로, 식을 정리해주면 다음 과정을 거쳐 선형방정식을 얻을 수 있습니다.


위 식의 해는 1계 선형 상미분 방정식을 푸는 방법으로 구하면 됩니다.

그렇게 해서 u(x)를 구했다면, 다시 y를 구하기 위해
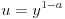
이놈을 이용해줍니다.
이 과정을 마치 공식을 외우듯이 외우는 건 절대로 추천하지 않습니다. 그럴 필요도 없고 외워봤자 얼마 안가고 다시 까먹을 게 뻔하니까요. 기억해야 할 것은 공식이 아니라 어떻게 치환했는지. 어떻게 선형방정식으로 유도가 되는지. 입니다
예제를 풀어보기 전에 이 일련의 과정을 다시 정리해봅시다

(ii) 예제풀이
(예제 1) 미분방정식의 해를 구하여라
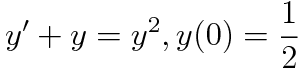
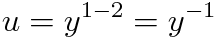
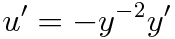
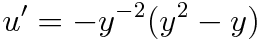
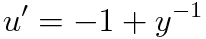
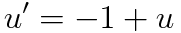
짜잔 이렇게 선형방정식을 만들 수 있습니다.
해를 구하는 다양한 방법이 있겠지만, 저는 간단하게 변수분리형으로 풀었습니다.
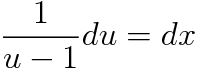
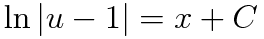
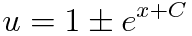
여기서 초깃값을 대입하면 끝납니다. 가 아니라!!
많은 분들이 여기까지 하고 끝내는 실수를 합니다. 마지막으로 다시 u를 y로 치환해주어야겠지요?
우리가 구해야 하는 건 u가 아니라 처음 미분방정식에 들어있던 y니까요
u=1/y로 설정했습니다. 따라서 주어진 미분방정식의 일반해는 다음과 같습니다.
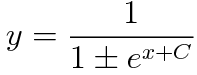
초깃값 y(0)=1/2를 적용해주면
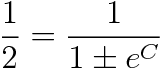
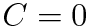
를 구할 수 있고, 또한 분모에 있는 ±가 +로 한정됩니다. 따라서 주어진 미분방정식의 특수해는 다음과 같습니다

(예제 2) 미분방정식의 해를 구하여라
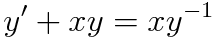
(a) u 설정
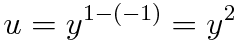
(b) 양변 미분
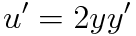
(c) 처음식 대입
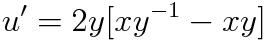
(d)u 다시 대입하고, 정리하기

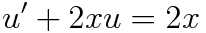
이것 또한 2x로 묶어서 변수분리형으로 풀 수 있는데요, 이번에는 1.5-1에서 배운 선형방정식의 해를 구하는 방법을 사용할게요
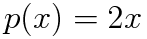
이므로 적분인자 I.F.는 다음과 같습니다.(적분 과정 생략)
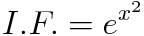
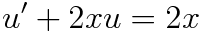
위 식의 양변에 적분인자를 곱해주면 다음 식을 얻습니다.
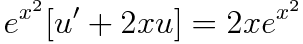
좌변이 적분인자와 u를 곱한 것을 미분한 꼴이기 때문에 양변을 적분하면 다음과 같습니다.
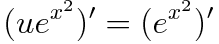
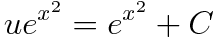

마지막으로 u를 다시 y로 치환해줍시다.
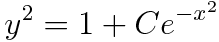
따라서 주어진 미분방정식의 일반해는 다음과 같습니다.
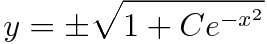
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 2.1-1 중첩원리 (Superposition Principle) (2) | 2023.01.04 |
|---|---|
| [공업수학] Homogeneous Linear ODEs of Second Order에서 중첩원리 증명 (0) | 2023.01.04 |
| [공업수학] 연립미분방정식 예제 : 비제차 방정식 (Nonhomogeneous Equation) (0) | 2023.01.01 |
| [공업수학] 1.5-1 선형 상미분방정식(Linear ODEs) (1) | 2022.12.30 |
| [공업수학] 1.4-3 적분인자(Integrating Factor) (2) | 2022.12.30 |