1. Separable Partial Differential Equations
변수분리라는 이름으로 불리는 가정입니다.
편미분 방정식을 풀기 위해 u(x,y)라는 함수가 x만의 함수와 y만의 함수의 곱으로 이루어져있다고 가정합니다.
당연히 그렇지 않은 해가 존재할 수 있겠지만 그러한 일반해를 구하는 방법이 아직까지는 발견되지 않았기 때문에 변수분리 가정에서 출발합니다.


아래의 heat equation을 예시로 보겠습니다.
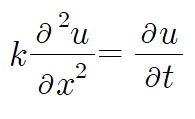
u를 x와 t의 함수라 가정한다면 다음과 같이 변수분리 가정을 할 수 있습니다.

양변의 편미분 항들은 아래와 같이 정리됩니다.
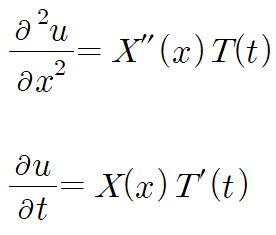
이를 주어진 방정식에 대입하고
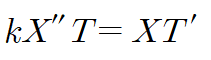
양변을 kXT로 나눕니다. (k로 나누는 것은 비교적 간단한 T'/T항에 상수k를 옮겨서 계산을 용이하게 하기 위함)
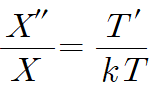
이것이 어떠한 상수 lambda와 같다고 합니다. 이때 이 상수를 "separation constant"라 합니다.
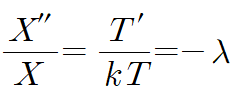
그러면 다음과 같이 두 개의 방정식으로 편미분 방정식이 분해됩니다.
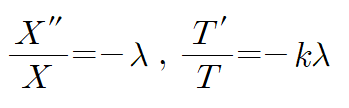
2. Solution of a PDE
변수분리 가정 이후 PDE(편미분 방정식)의 해는 다음과 같은 과정으로 구합니다.
(i) 변수분리한 함수를 미분방정식에 대입
(ii) λ 이용해 미분방정식 분리
(iii) 일반해 구하고 경계조건 적용
(iv) 초기조건 적용 후 정리 (푸리에 급수)
* 통상 경계조건을 먼저 적용합니다.
(예제 1) 편미분방정식의 해를 구하여라
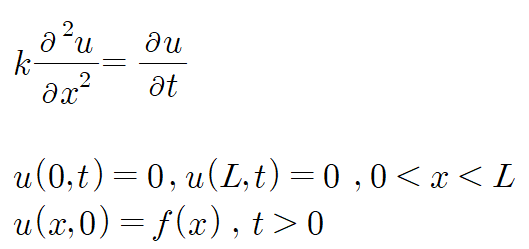
(i) 변수분리 후 미분방정식에 대입합니다.
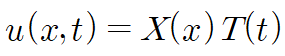
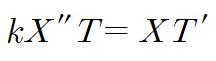
(ii) 이를 정리한 후 λ를 이용해 미분방정식을 분리합니다.
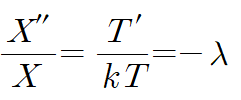

(iii) 통상 경계조건 -> 초기조건 순으로 적용합니다.
경계조건이 x에 대해 주어져 있으므로 X(x)를 먼저 구합니다.
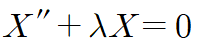
이때 λ의 부호에 관련한 분류 세 가지가 등장합니다.
- λ > 0
- λ = 0
- λ < 0
각각 아래와 같이 α 를 사용해 표현할 수 있습니다. 제곱이 등장하는 건 부호변화를 확실히 하기 위함과 미분방정식의 해를 깔끔하게 하기 위함입니다.
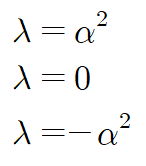
첫 번째 경우 (λ > 0)
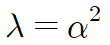
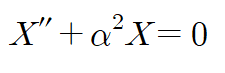
위 미분방정식의 일반해는 삼각함수들의 합으로 표현됩니다.
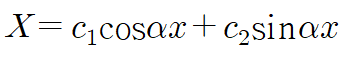
첫 번째 경계조건을 봅시다.
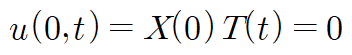
T(t) = 0 인 경우 즉 trivial solution 을 제외하면 x(0)=0이라는 것을 알 수 있습니다.
이를 적용하면 c1 = 0 이고
마찬가지로 X(L) = 0 을 적용합니다.
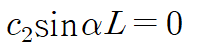
해당 삼각방정식의 해는 αL = nπ 일 때 이므로 α는 자연수 n을 사용해 다음과 같이 나타낼 수 있습니다.
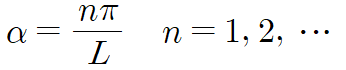
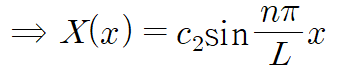
두 번째 경우(λ = 0) X'' = 0 이므로 X(x)는 일차함수가 됩니다.
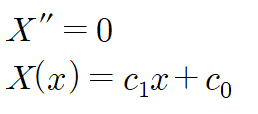
이 경우 경계조건을 만족하는 해는 자명해(trivial solution) X(x) = 0이므로 제외합니다.
세 번째 경우(λ < 0) X는 지수함수들의 합으로 표현됩니다.
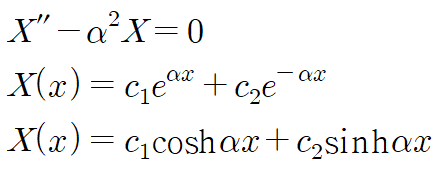
※ 첫 번째 경우와 세 번째 경우에서 미분방정식의 해를 구하는 과정이 생소하다면 아래 링크를 보고오세요
[공업수학] 2.2-2 상수계수를 가지는 제차 선형 상미분 방정식 예제
관련 포스팅 #공업수학 2.2-1에서 람다(λ)를 이용한 특성방정식을 통해 구할 수 있는 상수계수를 가지는 ...
blog.naver.com
이 또한 해당 문제에서는 c1 = c2 = 0가 되어버려서 결국 가능한 건 λ > 0 뿐입니다.
다음으로 T(t)를 구합니다
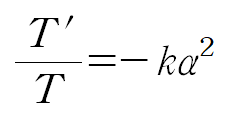
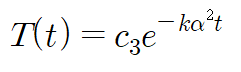
이것을 앞서 구한 α를 대입해 정리합니다.
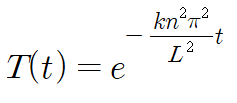
※ 위 1계 제차 상미분방정식의 해를 구하는 과정이 생소하다면 아래 링크를 보고오세요
[공업수학] 1.3 Separable ODEs (변수분리형 상미분 방정식)
간단한 변수분리형 1계 상미분 방정식을 풀어보자. 1.2는 방향장(direction field)에 관한 내용인데 깊게 들어가지 않고는 딱히 알 필요성이 적기 때문에 건너뛴다. 방향장이 뭔지 알고 싶은 사람은
subprofessor.tistory.com
(iv) 초기조건을 적용하기 전에 다시 하나로 u(x,t)를 합쳐줘야 합니다.
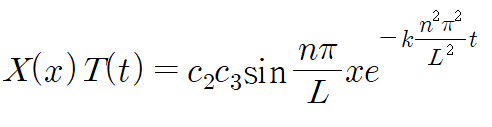
모든 n에 대해서 해가 존재하니 가능하니 이것을 하첨자 n을 써서 u_n 이라 표현합니다
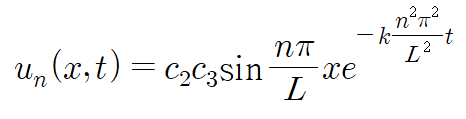
이것을 모든 n에 대해 합칩니다. 뒤에 나오겠지만 c2와 c3 이 그냥 상수가 아니라 n에 관련되어 있기 때문에 함부로 급수 밖으로 빼내선 안 됩니다.
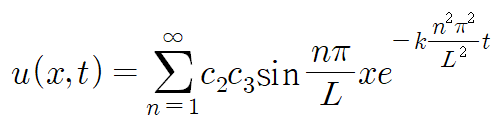
급수 형태로 표현한 후에 초기조건을 적용합니다.
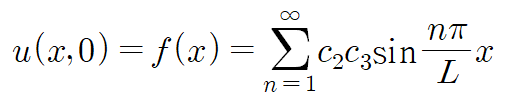
푸리에 사인 급수 형태이므로 계수 c2c3은 다음과 같이 표현할 수 있습니다.
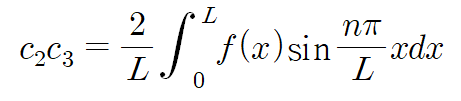
따라서 미분방정식의 해는 다음과 같습니다.

너무 복잡하게 보인다면 다음과 같이 정리해도 무방합니다.
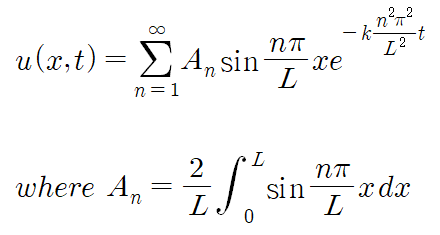
3. Using Fourier Transform
푸리에 변환은 아래 내용 참조
https://subprofessor.tistory.com/150
[공업수학] 푸리에 변환(Fourier Transform)
#공업수학 푸리에 변환과 푸리에 역변환은 다음과 같습니다. 1. 푸리에 변환 푸리에 변환은 다음과 같이 정의됩니다. 푸리에 변환의 경우 적분구간이 (-∞,∞) 이고 코사인,
subprofessor.tistory.com
비슷한 방법으로 라플라스 변환을 이용한 편미분 방정식 해법이 있습니다.
푸리에 변환을 이용해 편미분 방정식의 해를 구하는 절차는 다음과 같습니다.
(i) 변수의 범위와 초기조건을 고려해 푸리에 변환을 정의
(ii) 미분방정식의 양변에 푸리에 변환
(iii) 상미분 방정식의 해 구하기(경계조건 적용)
(iv) 푸리에 역변환을 수행하여 편미분 방정식의 해 구하기
(예제 2) 편미분방정식의 해를 구하여라

위와 같은 형태의 편미분 방정식을 라플라스 방정식이라 합니다.
(i) x와 y 중 무엇에 대해 푸리에 변환을 수행할 지 결정해야 합니다. y의 범위가 (0, ∞)이므로 y에 대해 푸리에 변환을 수행합니다.
또한 y의 초기조건이 도함수 형태로 주어져 있으니 푸리에 코사인 변환을 사용합니다.
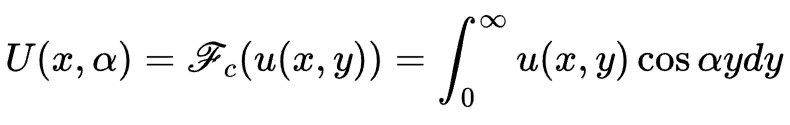
(ii) 주어진 양변에 푸리에 변환을 취하면 다음과 같습니다.

이때 도함수 공식과 0에 대한 변환이 0임을 사용하고 α 를 상수 취급합니다.
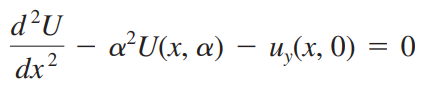
이때 y에 대한 초기조건을 적용합니다.

(iii) 위 상미분 방정식의 해를 구합니다.
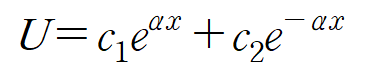
또는
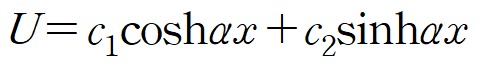
이때 x에 대한 경계조건을 고려하면 두 번째 쌍곡선함수(hyperbolic function)를 사용해 표현한 형태가 더 유용하다는 것을 알 수 있습니다.

위 경계조건에 푸리에 변환을 취합니다.
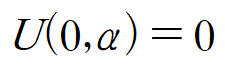
위 식을 상미분 방정식의 해에 적용합니다.
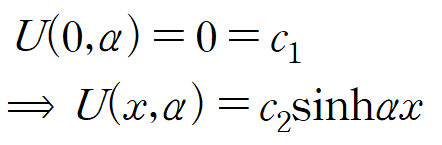
두 번째 경계조건을 적용합니다.
이때 아래 공식을 사용했습니다.
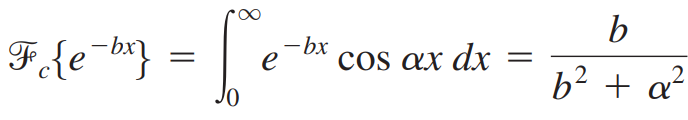
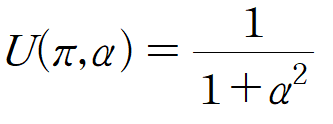
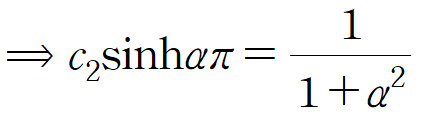
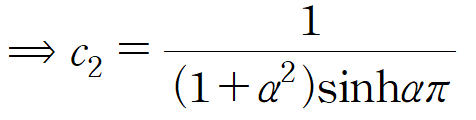
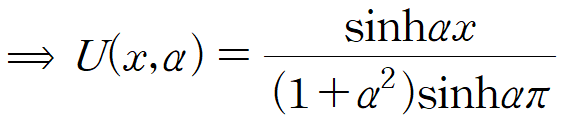
(iv) 푸리에 코사인 역변환을 수행하여 u(x,y)를 구합니다.

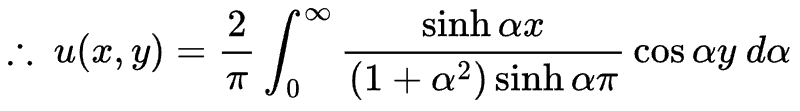
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 1.4-2 완전미분방정식 예제 (0) | 2022.12.29 |
|---|---|
| [공업수학] 1.4-1 완전미분방정식(Exact ODEs) (0) | 2022.12.29 |
| [공업수학] 푸리에 변환(Fourier Transform) (0) | 2022.12.27 |
| [공업수학] 1.3 Separable ODEs (변수분리형 상미분 방정식) (0) | 2022.12.27 |
| [공업수학] 1.1 미분방정식의 분류 (0) | 2022.12.26 |