슬슬 뜨악할 수준이 슬금슬금 보인다. 오늘 배울 완전미분방정식의 기반을 이루는 개념은 편미분과 관련이 있다. 편미분 관련 지식은 다음 블로그에서 참조하면 된다. 본 블로그와는 다르게 매우 친절히 소개하고있다.
https://blog.naver.com/mrhyde/60061507248
전미분, 편미분
편미분과 전미분 ∂ 는 편(偏)미분 기호입니다...여러 변수 중에서 1개의 변수에 대해서만 미...
blog.naver.com
솔직히 가독성은 조금 떨어지는데(..) 이번 1.4-1을 위해 알고있어야 하는 개념을 모두 담고있는 좋은 글이니 알고있던 사람도 한번 들어가볼것.
1. Basic Concept

x, y에 관한 다변수함수 z를 위와 같이 정의할 때, 미분소 dz는 아래와 같이 정의된다.

이것이 알아야 하는 전제이고,

위와 같은 형태로 정리되는 어떤 식에 대해서

라고 정리할 수 있으므로,

라는 해를 얻을 수 있다. 라는 게 오늘의 결론이다. 통상적으로는 다음과 같은

,

두 개의 식으로 묶어져있는 어떤 미분방정식.. 즉 아래와 같은 형태의 미분방정식일 때 "완전미분방정식인가?"하고 떠올리면 된다."

요런 놈들을 다루는 방법중의 하나가 바로 오늘 배울 "완전미분방정식" 이다.
즉 아래 형태의 미분방정식일 때 고려해보는 방법이다.

2. 완전미분방정식
다음 두 가지 조건을 만족시키면, 그 미분방정식을 "완전미분방정식"으로 정의한다.


그렇다. 전혀 감이 오지 않는다. 그게 정상이니 불안해하지 말자. 일단 완전성 즉 Exactness부터 알아야 하는데, (b)식의 의미부터 알아보자.


M과 N은 위와 같이 정의했다. 실제로 문제를 풀 때는 어떤 F에 대해서 저렇게 정의하는 느낌?이랄까 주어진 M과 N에 대해서 위 두 식이 성립하는 F가 존재한다고 가정하는 것이다. 그랬을 때, (b)식은 자연스럽게 아래와 같이 변한다.

엥 이건 당연한 거 아닌가? 아니다. 그렇지 않은 경우가 있으니까 따로 완전성을 정의한 것이다. 어디까지나 "그런 F가 존재한다고 가정"했을 뿐이다.

위 예시에 대해서는 완전성이 성립하지 않는다.(nonexactness) 차근차근 확인해보자. M과 N은 위의 경우 아래와 같이 정리된다.


이때 M과 N을 각각 y와 x에 대해 편미분 하면 다음과 같다.


애초에 "어떤 F에 대해 가정"한 것이므로 위와 같은 경우에는 완전성을 띄지 않는다. 즉 완전미분방정식이 아니다. 이번에는 완전미분방정식의 예를 보자

완전성 검사를 실시하면 다음과 같다. dx 앞에 있는 애들은 y로 편미분해주고, dy 앞에 있는 애들은 x로 편미분 해주면 된다.


편미분한 두 함수가 같으므로 본 미분방정식은 완전미분방정식이다. 느낌오나?
3. 완전미분방정식의 해
지금 공부하는 순서는 [기본 컨셉] => [완전미분방정식이란] => [완전미분방정식 풀기] 세 단계이다. 완전미분방정식의 해를 구하는 과정은 제법 길다. 하지만 어려운 개념은 아니다. 편미분한것처럼 반대로 어떤 변수에 대해서만 적분을 거꾸로 해주면 된다.(z=f(x,y)에서 x와 y가 독립변수일 경우만 취급하기 때문에 각각의 x,y적분에서 서로를 상수취급해도 무방하다.) 이건 좀이따 더 자세히 알아보고, 해를 구하는 순서부터 먼저 알아보자.

완전성 검사는 위에서 소개했고, 다음은 (b)단계다. 이 단계는 예를 통해 알아보는 게 더 이해가 빠르다. 한 개만 알아보고 다음 포스트에서 예제를 더 풍부하게 알아보자
(예제) 다음 미분방정식의 해를 구하여라

우리가 알고있는 형태로 만들어주자. 왼쪽으로 dx와 dy 를 몰아서 정리해주면 다음과 같다.


완전미분방정식 형태이므로 완전성 검사를 실시해보자. M과 N은 다음과 같다.


M과 N을 각각 y와 x로 편미분 해주면 아래와 같은 결과를 얻는다.


따라서 해당 미분방정식은 완전미분방정식이다.

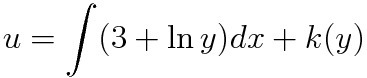
위와 같이 u(x,y)를 세울 수 있다. 매애앤 처음에 예시로 든 z=F(x,y)에서 단순히 z대신 u로 바뀐 것이다. (왜 그런지는 잘 모르겠는데 교재에서는 u를 더 좋아하는 것 같아서 u로 예제를 내봤습니다.) 여기서 한 가지 유연한 사고를 가질 필요가 있다. 만약 위 방법대로 M을 적분하고 k(y)를 가정해서 u를 세웠는데 풀이가 영 답답하고 꼬여간다면 거꾸로 해보자. 즉 N을 y에 대해 적분하고 k(x)를 가정해서 풀면 된다.

이렇게
다시 문제로 돌아오자

이와 같이 적분할 수 있는데, 적분상수는 나타내지 않는다. 뭐 나타내도 되는데.. 이유는 마지막에 나오니 끝까지 집중!! :)

이제 마지막! (b)단계에서 세운 u를 y에 대해 편미분해주면 된다. 엥 편미분을 갑자기 왜하징.. 싶을텐데 우리가 처음에 N을 정의할 때 u를 y로 편미분한 것으로 N을 정했기 때문에 그 N과 비교하기 위함이다. 에잉 모르겠어 싶으면.. 일단 끝까지 보자

이 관계식을 이용합니다
위 관계식은 처음 우리가 u를 가정하고, N을 잡을 때 세운 관계식이다.(가정이었지만 완전성으로 인해 증명이 됨)

N은 위와 같고 u를 y에 대해 편미분해주면 다음 식을 얻는다.

이제 위 관계식을 이용해보자

와우! 깔끔하게 소거가 된다. 양변에 x/y를 날려주면

음! 간단하게 양변에 y로 부정적분을 취해주자(이 때도 적분상수는 취급하지 않는다)

거의 다왔다. 이제 u를 정리해주면 진짜 끝!
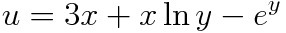
이라고 생각했지만 찐막 스텝이 남아있다.(..?)
우리가 처음에, 제일 처음에 완전미분방정식의 basic concept라고 배웠던 걸 다시 떠올려보자
dz=0꼴에서 z=c를 도출했던 게 기억나는가? 혹시 가물가물하다면 위로 스크롤을 올려서 직접보자(가물가물할 때 직접 그 부분을 펼쳐서 복습하는 습관은 항상 학생들에게 추천하는 좋은 공부방법이다.)
즉, 우리가 풀어오는 이 solution의 과정 속에는 u=C라는 식이 숨어있던 거다! 우변이 상수 C이기 때문에 중간 과정에서 적분상수를 생략해도 무방한 것이고. 찐찐막 정리를 해주면 다음 해를 얻을 수 있다.

끝! 우리가 편하게 받아들이는 형태는 아니지만 도함수가 없는 관계식을 도출해냈다. 이게 미분방정식을 푸는 것이다. 추가로 초깃값이 주어진다면 당연히 적분상수 C를 처리할 수 있다. 애초에 이 소단원의 제목이 Exact ODEs(상미분 방정식) 라는 것을 떠올리면 u(x,y)꼴의 다변수함수 해는 나오면 안되는 것이고, 이 단원에서는 양함수(explicit function)꼴의 해보다는 음함수(implicit function)꼴의 해가 더 많이 등장한다.
이제 좀 새로운 것을 배우는 기분이 들 시기인데 나는 처음에 이 챕터를 처음보고 너무 이해가 안되서 손을 아예 놨다가(시작한지 하루만에..) 한 달 뒤에 다시 도전해서 직접 해를 구하는 짜릿한 경험을 했는데 정말 형언할 수 없는 쾌감이었다. 이 쾌감이 나를 계속해서 새로운 학문의 문으로 이끈다. 나는 한 번 좌절을 맛본 사람을 위해서 포스팅을 하지 않는다. 다시 일어서는 사람을 위해서 내 귀한 시간을 할애한다. 그러한 과정에서 도움받기를 바라는 마음이다. 나의 서툰 글솜씨와 얕은 지식으로 인해 온전히 전달되지 않는 부분이 많을 거라고 생각하기 때문에 읽어주는 사람들이 더 고맙고 어떻게 하면 쉽게 풀어 설명할 수 있을지 고민하게 된다.
<1.4-(1) 완전미분방정식 요약>

'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 1.4-3 적분인자(Integrating Factor) (2) | 2022.12.30 |
|---|---|
| [공업수학] 1.4-2 완전미분방정식 예제 (0) | 2022.12.29 |
| [공업수학] 편미분 방정식 (1) : 변수분리부터 푸리에 변환까지 (2) | 2022.12.27 |
| [공업수학] 푸리에 변환(Fourier Transform) (0) | 2022.12.27 |
| [공업수학] 1.3 Separable ODEs (변수분리형 상미분 방정식) (0) | 2022.12.27 |