이번 챕터는 완전미분방정식이 아닌 애들을 완전미분방정식으로 만들어주는 적분인자에 대해서 알아봅시다. Basic Concept는 그러한 함수 F가 있다고 가정하고 완전성 검사를 통해서 F를 구하는 느낌입니다. 그 뒤는 완전미분방정식의 해를 구하는 방법과 동일합니다.
(i) Basic Concept
Basic Concept는 이렇습니다. 완전미분방정식이 아닌 것에 완전성을 부여한다. 미지의 함수 F로 말입니다.
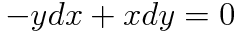
위와 같은 미분방정식을 예로 들어봅시다. 완전성 검사를 시행했을 때, nonexactness임을 알 수 있는데요, 이 식의 양변에 1/x^2 즉
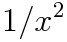
를 곱해줍시다. 그러면 다음과 같은 식이 되는데요
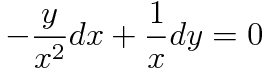
이 식은 완전성을 가짐을 직접 해봄으로써 알 수 있습니다.(꼭 해보세요!)
느낌오시나요? nonexact - ODE에 어떤 함수를 곱해주니 exact - ODE가 되었습니다. 이와 같이 곱해주는 어떤 함수를 바로 적분인자(Integrating Factor)라고 합니다. 마스터키와도 같은 느낌을 물씬 풍기는 요 적분인자를 어떻게 설정하면 좋은지를 알아봅시다.
(ii) 적분인자의 설정(How To Find I.F?)
다음과 같은 미분방정식을 생각해봅시다.
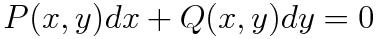
이때, 위 미분방정식은 완전성을 갖지 않는 미분방정식이라는 걸 알고 있는 상태입니다. 이 식의 양변에 어떤 함수 F를 곱해줍시다.

이렇게 말이죠. 이 F를 곱해준 새로운 식이 완전성을 가지는 미분방정식이라고 가정해보는 겁니다. 다른 말로, 완전미분방정식이 되게 하는 어떤 함수 F를 양변에 곱해주는 겁니다.
이제 다음으로는 완전미분방정식이라는 가정을 검증하기 위해서 실제로 완전성검사를 해봅시다.
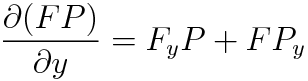
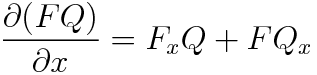
이렇게요. 근데 우리가 F를 설정함에 있어서 F(x,y)라고 설정해버리면 즉 F가 x와 y로 이루어진 2변수함수라고 가정한다면 계산과정도 복잡해질 뿐더러, 실제로 F를 구하기가 매우매우 어려워집니다.(Non-Helpful) 그래서 F를 F(x)또는 F(y)로 가정합니다. 일단 F=F(x)라고 가정하고 식이 간단하게 정리가 안 될 시 F=F(y)라고 가정하고 다시 풀면 됩니다. 둘 다 가능한 경우도 있고, 둘 중 하나만 적용가능한 경우가 있으니 직접 해보시고 적절하게 F를 설정해주시면 되겠습니다. 일단 F=F(x)라고 가정하고 진행해볼게요
① F=F(x)라 가정
F=F(x)라고 가정한다면, F를 y에 대해 미분한 것은 0이됩니다. 따라서 다음과 같은 식을 얻을 수 있어요
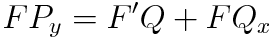
이제부터가 조금 복잡합니다. 아 어디까지나 익숙하지 않을 때 복잡하다는 뜻이예요. 여러 번 보고 좋은 예제들을 많이 풀다보면 유도과정은 익숙해집니다. 공식처럼 외우려고 하지말고 식에서 다음 식으로 넘어가는 Concept를 잘 캐치하시면 보다 유익한 배움의 과정이 됩니다.
위 (a)식의 양변을 FQ로 나눠주면 아래와 같은 식을 얻을 수 있고 F에 대해서 정리하는 일련의 과정은 다음과 같습니다.

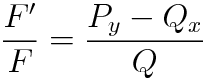
(a)의 양변을 FQ로 나누어주는 이유를 공식처럼 외우려고 하지마세요. 왜 FQ로 나누었을까? 라는 물음을 스스로 던져봅시다.
이번엔 식의 간결성을 위해 우변을 R이라고 간단히 정의합시다.
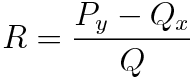
그러면 F는 다음과 같이 정의됩니다. 먼저 양변을 적분하면 좌변이 lnF가 되는데 자연로그를 벗겨주면 아래 (f)식을 얻을 수 있어요

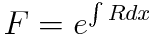
이렇게 적분인자를 구해주시면 됩니다. 너무 어렵고 복잡하다구요? 네 맞아요 너무 복잡해요. 실용성도 없어보인다구요? 유갑스럽게도 맞습니다. 적어도 저의 경우에는 아직까지 한 번도 역학분야에서 이를 활용해본 적이 없습니다. 하지만 이러한 일련의 과정을 익혀나가는 것은 배우는 사람으로 하여금 수학적 사고를 심어주고 유연한 문제해결능력을 길러줍니다. 항상 학생들을 가르칠 때마다 일련의 과정에 담긴 의미 하나하나에 집중하다보면 어느 순간 부쩍 성장해있는 자신을 볼 거라고 늘 힘주어 말합니다.
(b)의 식을 도출하는 과정에서 (a)식의 양변을 FQ로 나누었습니다. FP도 아닌 왜 하필 FQ일까. 다들 생각해보셨나요? 답은 F를 구하기 위해서 입니다. 우리가 F를 구하기 위해서 (a)식을 변형시켰는데, F'/F꼴로 정리할 수 있다는 걸 수학자들이 본 거죠. 왜? lnF의 미분꼴이니까 그렇게 정리해준 겁니다. 어떻게 보면 당연한 이야기를 계속 하고있는데, 다음 F=F(y)라고 가정하고 풀 때는 FQ로 나눠주지 않겠구나 하는 생각이 자연스럽게 든다면 아주 바람직한 학습태도를 가지고 있다고 자부하셔도 될 것 같습니다. 아주 좋아요
F=F(y)라고 가정하고 푸는 방법을 슥 알아보고 얼른 예제를 풀어봅시다.
② F=F(y)라 가정
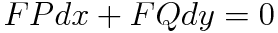
이 식에서 F=F(y)라고 가정하고 완전성 검사를 실시합니다.
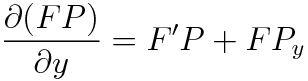
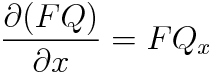
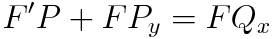
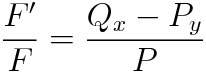

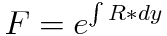
F=F(x)인 경우와 구분하기 위해서 R대신에 R*(R star)로 표기하였습니다.
(iii) 예제풀이
(예제 1) 다음 미분방정식의 해를 구하여라
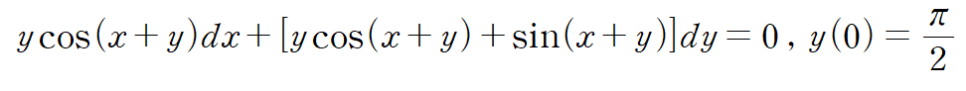
뭔가 복잡해보이죠. 완전미분방정식 형태이기 때문에 일단 완전성검사부터 실시해줍시다.
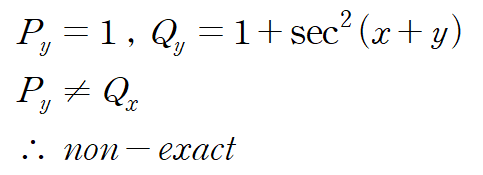
완전성을 따져보니, 위 미분방정식은 완전미분방정식이 아닙니다.
그렇다면 적절한 적분인자를 구해서 완전미분방정식 꼴로 만들어주어야 하는데, 그게 그렇게 쉽지가 않습니다.
먼저 F=F(x)라 가정하고 F를 찾아봅시다. 굳이굳이 식유도를 다시하진 않겠습니다.
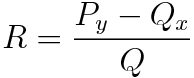
기억나지요?
본 예제에서 Py와 Qx를 찾아 대입해주면 R이 정리됩니다.
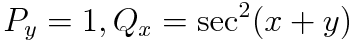
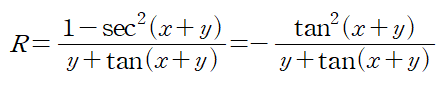
R의 형태가 매우 복잡해 적분을 할 수 없습니다.
이럴 때는 통상 적분인자가 x로 이루어진 함수가 아니라 y로 이루어진 함수일 거라 가정하고 다시 구하면 됩니다.
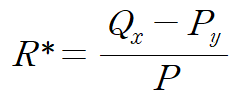
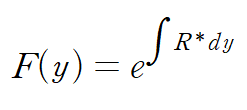
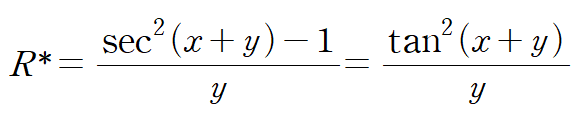
F=F(y)라 가정하고 풀었음에도 불구하고 또다시 적분불가한 형태를 얻었습니다.
앞선 두 가지 결과는 적분인자가 F(x)나 F(y)와 같이 단일변수만을 가지는 함수가 아닐 수 있다는 것을 시사합니다.
즉, 주어진 방정식을 완전미분방정식으로 만드는 적분인자에는 x와 y가 섞여있을 가능성이 높다는 것이죠.
공식을 통해 적분인자를 얻을 수 없으니, 주어진 꼴에서 적절히 미분방정식을 변형시켜 봅시다.
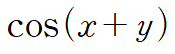
cos(x+y)를 양변에 곱하면 완전미분방정식을 얻을 수 있습니다.
직관적으로 알기는 쉽지 않지만 tan(x+y)를 보고 분모의 cos(x+y)를 곱한다는 생각을 떠올리는 게 불가능하지만은 않습니다.
양변에 곱해주면 다음과 같이 미분방정식이 변합니다.
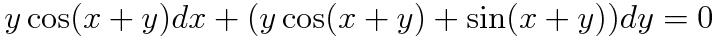
완전성 검사를 실시합니다
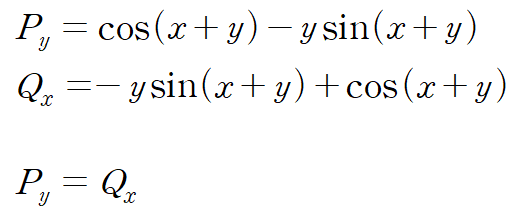
다음으로는 우리가 완전미분방정식의 해를 구하는 일련의 과정 a-b-c를 적용해줍시다. (완전성 검사 a는 건너뜀)

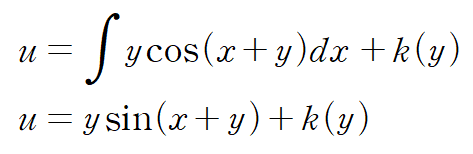

u를 y에 대해 편미분하면 다음과 같습니다
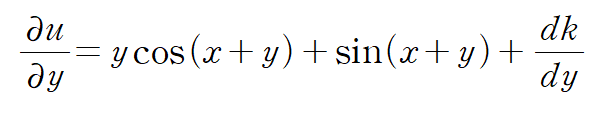
이때 우변=N (dy앞) 임을 이용하면
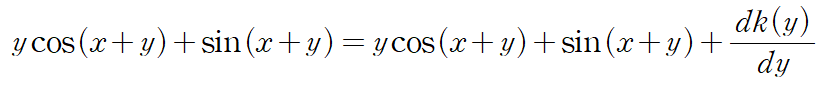
ycos(x+y)+sin(x+y)가 소거됩니다.
따라서 다음과 같이 정리할 수 있으며,
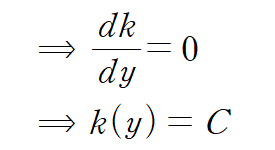
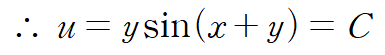
여기에 초기조건 y(0)=π/2를 적용하면

주어진 미분방정식의 해를 구할 수 있습니다.
<1.4-3 적분인자(Integrating Factor) 요약>
'MATHEMATICS > 공업수학' 카테고리의 다른 글
| [공업수학] 연립미분방정식 예제 : 비제차 방정식 (Nonhomogeneous Equation) (0) | 2023.01.01 |
|---|---|
| [공업수학] 1.5-1 선형 상미분방정식(Linear ODEs) (1) | 2022.12.30 |
| [공업수학] 1.4-2 완전미분방정식 예제 (0) | 2022.12.29 |
| [공업수학] 1.4-1 완전미분방정식(Exact ODEs) (0) | 2022.12.29 |
| [공업수학] 편미분 방정식 (1) : 변수분리부터 푸리에 변환까지 (2) | 2022.12.27 |