열역학 문제를 푸는 데 있어서 중요한 속성인 압력과 체적, 온도는 서로 긴밀한 관계를 맺고 있습니다. 열역학적 속성 간의 관계식을 찾기 위해 많은 과학자들이 약 200년 전부터 노력해온 덕에 이상기체 방정식, 반 데르 발스 방정식과 같은 여러 상태 방정식(Equation of state)들이 도출될 수 있었습니다. 오늘은 그 중에서 가장 심플하고 직관적인 "이상기체 방정식"을 알아봅시다.
(i) 이상기체의 정의
다음과 같은 가정을 만족하는 기체를 "이상기체"라고 합니다.
① 탄성충돌 외 다른 상호작용이 없다고 가정
② 기체의 각 분자를 점 입자(부피를 차지하지 않는 것으로 가정)라고 가정
위 두 가지 가정을 적용할 경우 기체의 압력과 체적, 온도 사이의 관계식이 매우 간단해집니다. 허나 어디까지나 "가정"이기 때문에 실제 기체의 물성치와는 오차가 발생합니다. 기본적으로 온도가 높고 압력이 낮을수록 이상기체에 근사합니다. 각 기체마다 물성치가 상이하기 때문에 절대적인 압력과 온도 하에서 실제기체가 이상기체에 근사한다고 말할 수는 없습니다.

물의 T-V다이어그램과 이상기체에 수렴하는 영역(T-V diagram for water)
위 T-V 다이어그램에서도 볼 수 있듯이 압력이 낮을수록, 온도가 높을수록 이상기체 영역에 포함됩니다.
+) T-V 다이어그램을 보는 방법은 따로 설명하지 않겠습니다. 간단히 빗금친 노란색 영역이 기체 영역이라고 이해하시면 됩니다. 또한 가로축의 V는 기체의 체적이 아닌 단위 질량당 체적인 비체적입니다.

(ii) 이상기체 방정식
이상기체 방정식은 다음과 같습니다.

P는 기체의 압력, V는 기체의 체적(부피), m은 기체의 질량, R은 기체상수(기체마다 다름), T는 기체의 절대온도(K)입니다.
이번에는 이상기체 방정식을 약간 변형해봅시다.
1) 양변을 m으로 나누면 다음과 같이 비체적( 체적/질량 ) 으로 V가 대체됩니다.

2) 기체상수 R을 몰질량과 기체의 표준기체상수(Universal gas constant)로 대체할 수 있습니다.


기체상수 R은 표준기체상수 Ru 를 기체 분자의 몰질량 M으로 나눈 것입니다.
이때 질량 m은 기체 분자의 몰질량 M과 기체 분자수 n을 곱한 것과 같으므로

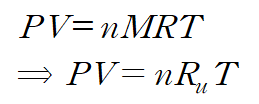
PV=nRT라고 할 때는 기체상수를 통상 이 표준기체상수로 한 것이고, PV=mRT라고 할 때는 각 기체에 대응하는 기체상수로 사용한 것입니다.
(iii) 이상기체 방정식의 응용
유체역학에서 압축성 유체의 압력분포를 구하는 과정에서 이상기체 방정식이 사용되었습니다. 밀도를 압력과 온도로 치환하는 방식으로 응용되었는데 이번에는 한 물성치를 다른 두 물성치로 치환하기보다 "두 상태에서 압력과 체적, 온도를 비교" 해봅시다.
열역학에서 한 시스템(계)에 대해 두 상태를 비교하는 일은 자주 등장합니다. 이때 이상기체 방정식을 응용한다면 두 상태 간에 기체의 압력, 체적, 온도를 다음과 같이 나타낼 수 있습니다.
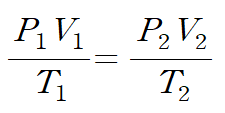
위 관계식의 유도는 이상기체 방정식의 양변을 T로 나누면 끝납니다.
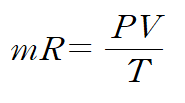
기체상수는 기체마다 일정한 값을 가지는 상수이고, 시스템 내에서 기체의 질량이 일정하다면 PV/T는 시스템에서 항상 같은 값을 가지게 됩니다. 때문에 위 식을 사용하면 초기상태로부터 다음상태의 물성치를 계산하는 것이 매우 간단해집니다.
(예제)
부피가 일정하게 유지되는 실린더가 있다. 실린더 내부의 기체에 대해 초기상태 온도와 압력이 각각 25℃, 100 kPa 라고 가정하자.
실린더 내부의 기체를 가열해 100℃에 도달했을 때의 압력을 구하여라

이상기체 방정식의 응용식을 사용합시다. 위 문제에서 주어진 기체의 종류는 중요하지 않습니다. 기체의 종류가 변하지 않으며 질량 또한 변하지 않으니, PV/T 가 일정함을 사용합시다.
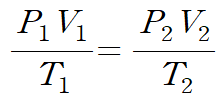
위 식에서 부피 V가 일정하므로 다음과 같이 압력을 정리할 수 있습니다.
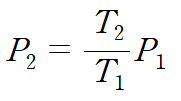
T에 대입하기 전 주어진 온도의 단위가 ℃ 이므로 절대온도 단위인 K 로 바꾸어 주어야 합니다.
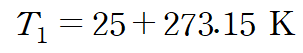
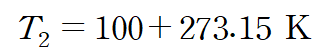
항상 온도는 "절대온도"를 사용합니다.
이를 대입하면
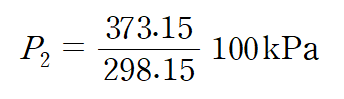
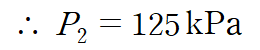
위와 같은 결과를 얻을 수 있습니다.
Any Qustions, Any Comments are WELCOME :)
오타나 오류 지적 감사히 받습니다
'기계공학 > 4대 역학' 카테고리의 다른 글
| [열역학] 고체, 액체에서의 엔트로피 변화 (0) | 2022.06.01 |
|---|---|
| [열역학] 압축인자 (Compressibility factor, Z) (0) | 2022.04.30 |
| [열역학] 순물질의 상 결정하는 방법 / 테이블에서 P,v,T 물성치 구하기 (0) | 2022.04.26 |
| [재료역학] 3. 전단력 선도와 굽힘모멘트 선도 (SFD, BMD) (1) | 2021.04.18 |
| [유체역학] 압축성 유체의 압력분포 (2) | 2021.04.14 |