열역학에서는 주로 순물질을 다루게 되는데 압력(pressure)과 비체적(specific volume), 온도 사이에는 긴밀한 관계가 있습니다. 그 관계는 Saturation curve를 중심으로 해석되니 먼저 P-T 선도(diagram)와 T-v 선도를 읽을 수 있어야 합니다.
두 선도를 읽는 방법에 대해 간략하게 설명하고 P,v,T 세 가지 중 두 가지 물성치가 주어졌을 때 나머지 하나를 구하는 방법을 소개하겠습니다.
※포화온도와 포화압력에 대한 설명은 아래 게시글 참조
https://subprofessor.tistory.com/41?category=933247
[열역학] 1. 포화온도, 포화압력
#열역학 물성을 따질 때, 다른 언급이 없다면 순물질이라 가정합니다. 이번 글에서는 Saturation temperature와 saturation pressure에 대해 알아봅시다. Saturation temperature는 포화온도라고 번역되..
subprofessor.tistory.com
(i) P-T diagram
P-T 선도는 일정한 P에 대해 온도를 높일 때 일어나는 상변화를 나타낸 것입니다.
아래 그림을 보면 같은 형상(질량)의 추가 실린더 위에 올라가 있습니다. P = F/A 인데 F = mg 로 일정하고 단면적 또한 일정하니 압력이 일정한 등압과정(isobaric process)이라 할 수 있겠습니다.
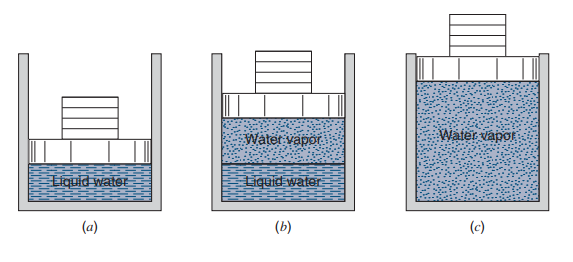
계속 가열을 하다보면 그림(b)처럼 액체의 일부가 기체상태가 됩니다. 또한 내부에서 기화가 일어나는 동안 온도가 일정하게 유지되는데 이와 같이 액체가 기체가 되어가거나 반대의 상태를 포화(Saturation) 또는 포화 상태라 하며 이 때의 온도를 Saturation temperature 라 합니다. 끓는 점(boiling point) 이라고도 하며 고체가 아닌 액체와 기체 간의 상전이만 의미합니다.
P-T 선도는 일정한 압력 하에서 Saturation이 일어나는 온도에 점을 찍어 연결한 곡선(Saturation curve)입니다.
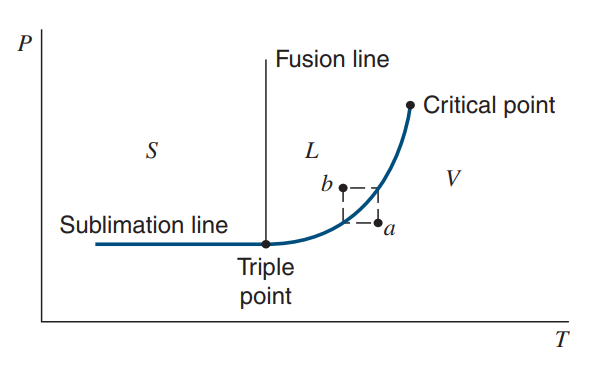
a 지점은 기체, b 지점은 액체입니다. (S : Solid, L : Liquid, V : Vapor)
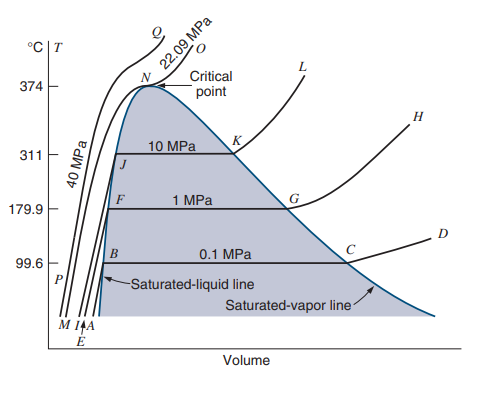
P-T 선도를 읽는 방법은 다음과 같습니다.
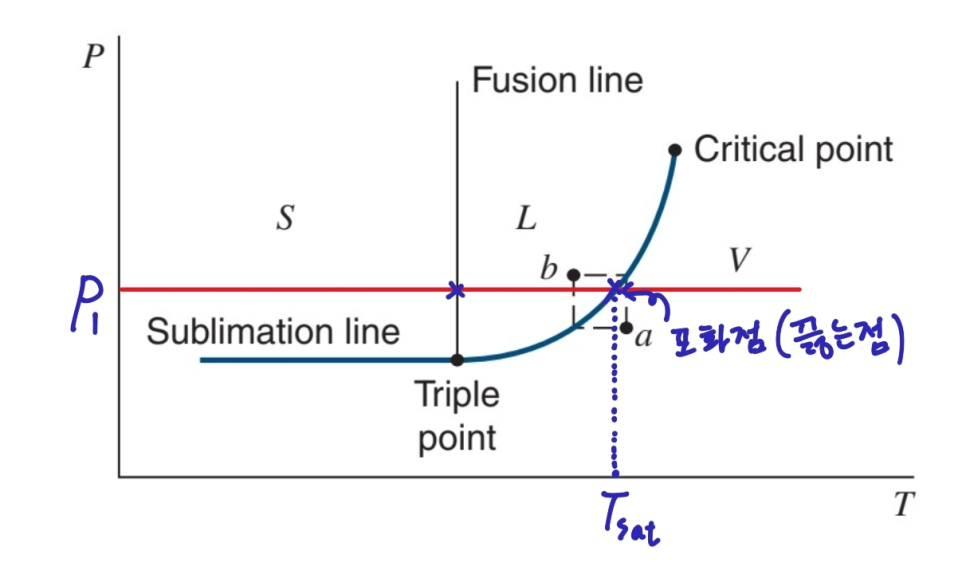
주어진 압력에 대해 가로선을 그리고 Saturation curve 와의 교점보다 주어진 온도가 높은지, 낮은지 판단합니다.
만약 높다면 기체 상태이며, 낮다면 액체 상태입니다.
이때 기체를 superheated vapor, 액체를 compressed liquid 라 부르기도 합니다.
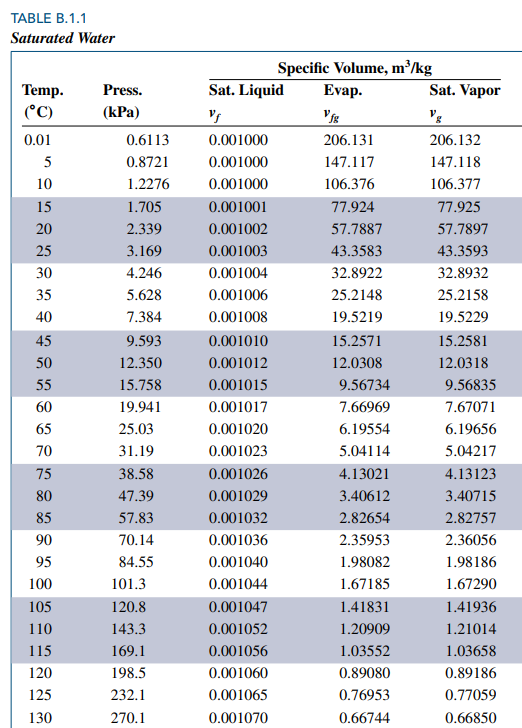
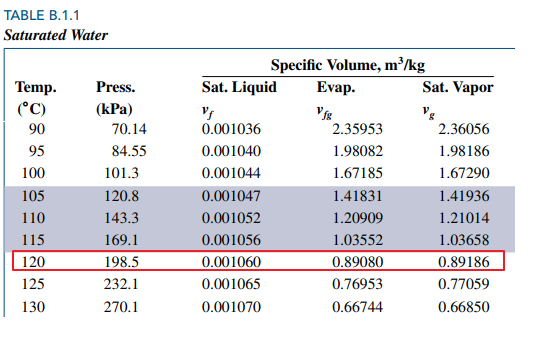
아래 표는 water에 대해 saturation temperature와 각각에 대응하는 saturation pressure와 비체적(specific volume)을 정리한 것입니다.
Pressure = 101.3 (대기압) 에서 saturation temperature 가 섭씨 100도 임을 확인할 수 있습니다.
비체적 열을 보면 vf, vfg, vg 세 가지 열을 볼 수 있습니다.
vf 는 포화상태인 순물질이 액체 100% 일 때의 비체적을, vg 는 기체 100%일 때의 비체적을 의미합니다.
vfg는 vg - vf 이구요
아래 표는 압력에 대한 saturation temperature를 나타낸 것입니다.
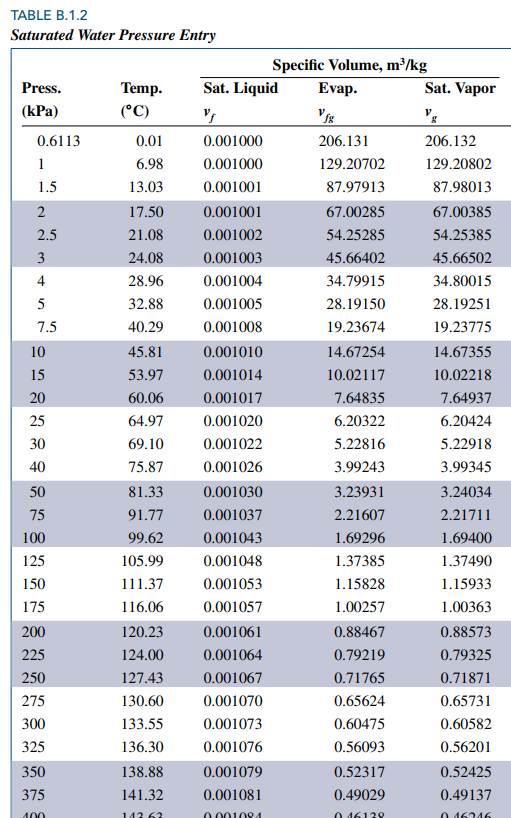
위 두 표를 이용해 under saturation 인 순물질에 대해 P-v-T 값을 구할 수 있습니다.
(ii) T-v diagram
T-v 선도도 동일하게 일정한 압력 하에서 온도와 비체적의 관계를 그린 곡선으로 이때 saturation 이 일어나는 지점은 가로방향 직선들의 모임인 산 모양 영역입니다.
아래 그림은 P = 1 atm(대기압, 101.3 kPa) 에 대해 온도 T를 높이는 등압과정을 진행했을 때 T-v 곡선입니다.
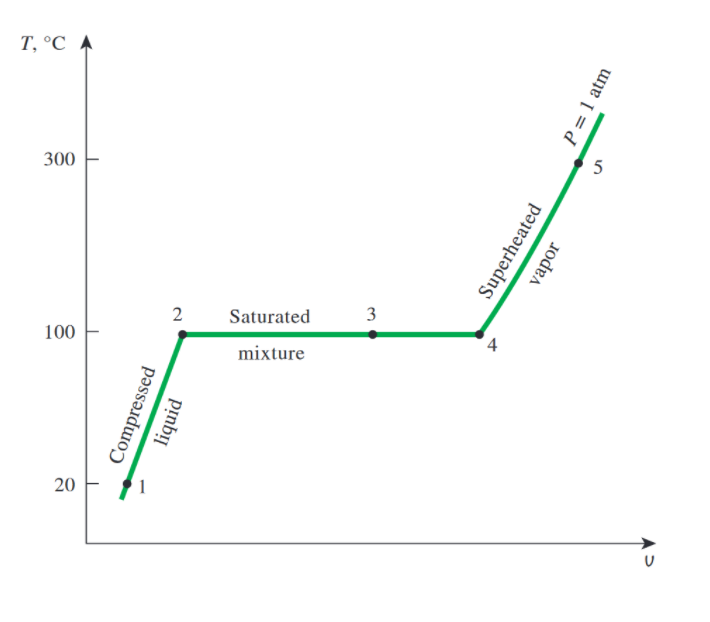
2지점에서 4지점까지의 상태가 saturation 이며, 2지점에 해당하는 비체적이 위 테이블에서 본 vf, 4지점에 해당하는 비체적이 vg입니다.
T-v 선도는 보통 T와 v가 주어졌을 때 사용하며
산 영역 오른쪽에 있다면 vapor, 왼쪽에 있다면 liquid 라 판단합니다.
아래 그림은 Liquid, Vapor, Saturation 영역을 나타내고 있으며 각 영역에 대해 해당 테이블을 읽으면 된다는 것입니다.
제가 가진 교재에서는 Liquid 상태일 경우 B.1.4 를 참조하라네요.
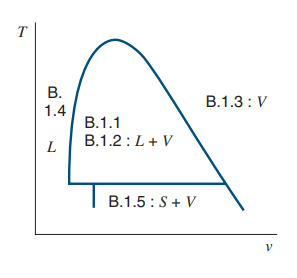
(iii) how to determine phase
(예제 1) 다음 P,T 에 대해 테이블을 이용해 물의 상을 결정하여라
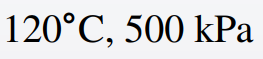
먼저 섭씨 120 도에서 포화압력을 알아야 하니 첫 번째 테이블을 봅시다.
섭씨 120도에서의 포화압력인 198.5 kPa보다 높은 압력 500 kPa 인 상태인 건데 P-T 선도를 봅시다.
아래 그림과 같이 문제의 상황을 이해할 수 있습니다.
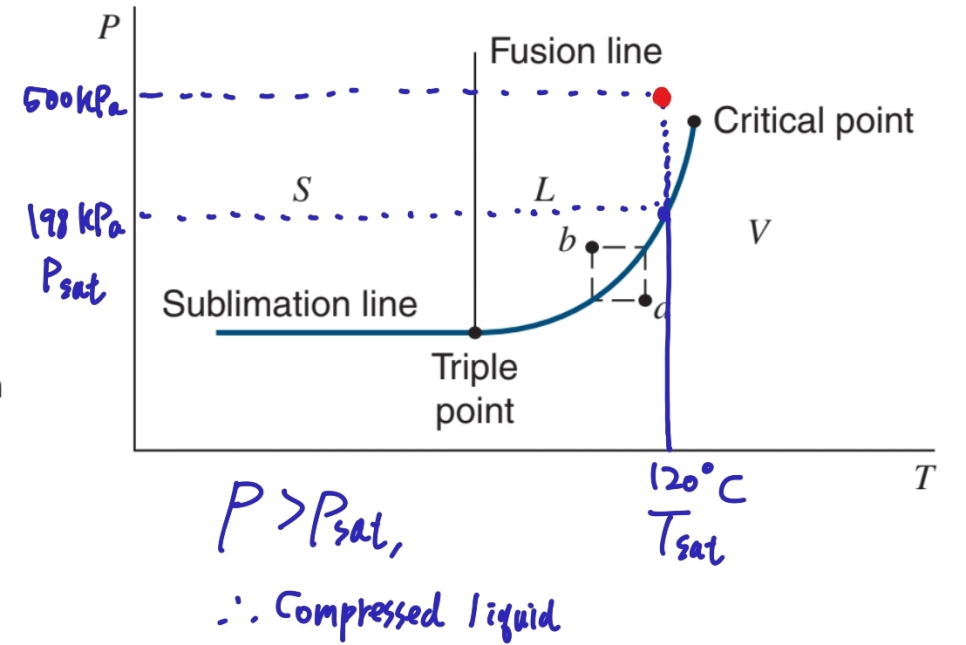
P-T 선도로부터 Liquid임을 알 수 있습니다.
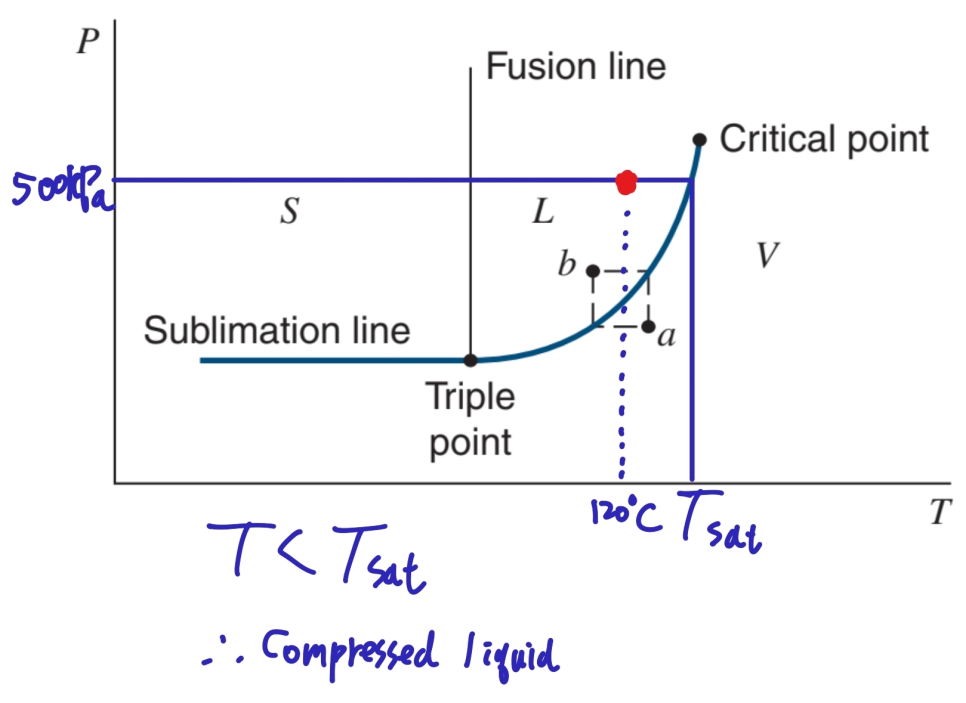
만약 온도가 아니라 압력을 사용한다면 두 번째 Table을 이용할 수 있습니다.

500kPa 에서 Saturation Temperature가 섭씨 151.86 도인데 그것보다 낮은 120도이므로 액체임을 알 수 있습니다.
(예제 2) 다음 T,v 에 대해 테이블을 이용해 물의 상을 결정하여라

첫 번째 테이블에서로부터 saturation이 시작되는 비체적(vf)과 끝나는 비체적(vg)을 얻을 수 있습니다.
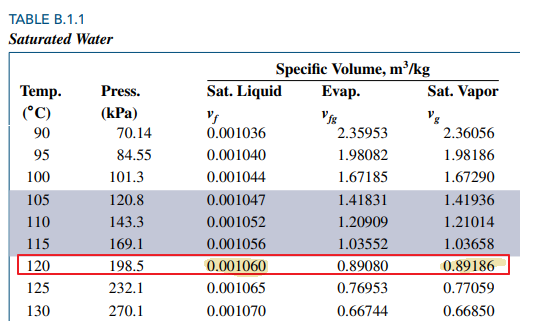
이때 vf<v<vg 이므로
Saturation, 즉 포화상태임을 알 수 있습니다.
추가적으로 압력이 198.5 kPa라는 것도 알 수 있구요.
(iv) How to determine P,v,T from TABLE
P, v, T 중 두 가지를 알고 있을 때 다른 하나를 알아내는 방법은 다음과 같습니다.
(i) 포화상태인지 확인한다.
(ii) 포화상태라면 테이블에서 각 물성치에 대응하는 값을 얻는다.
(iii) 포화상태가 아니라면 액체, 기체인지 상을 결정한다.
(iv) 각 상(phase)에 대해 주어진 table로부터 적절한 값을 얻는다.
(v) 필요하다면 주어진 물성치를 포함하는 구간으로부터 선형근사해서 물성치를 구한다.
(예제 3) 섭씨 30도, 1,000 kPa 암모니아의 비체적을 구하여라

먼저 암모니아 포화 테이블로부터 포화상태인지 확인합니다.
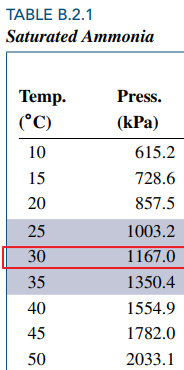
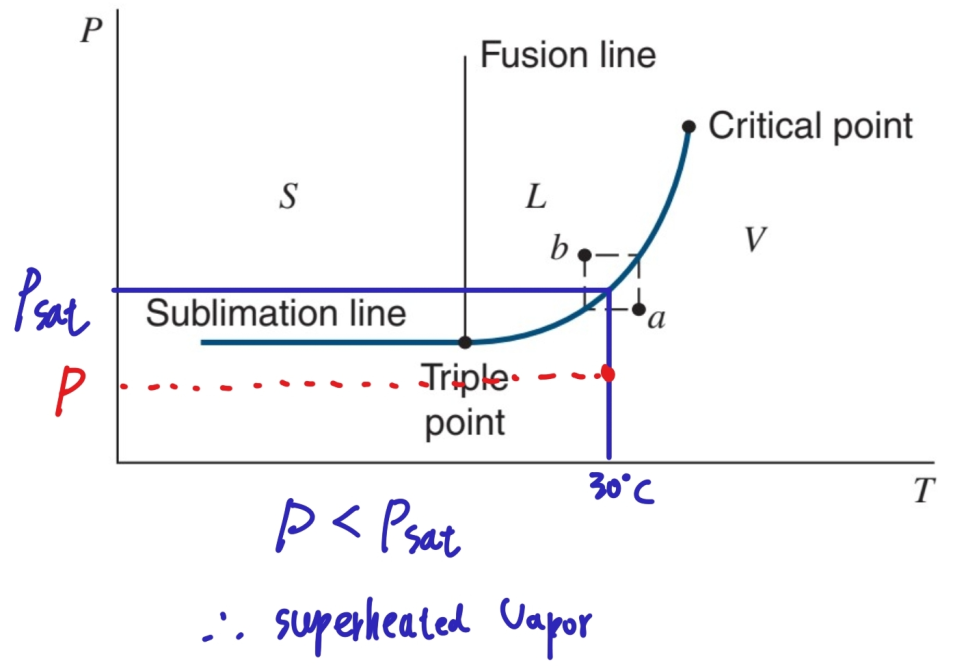
1,000 kPa는 포화압력인 1,167 kPa보다 작으니 기체임을 알 수 있습니다. (P-T 선도 이용)
주어진 물성치에 대해 암모니아가 기체로 존재함을 알았으니 Superheated ammonia 테이블로 가서 살펴봅시다.
아래와 같이 일정한 압력에 대한 물성치들이 주어져있음을 확인할 수 있습니다.
문제에서 주어진 물성치가 1,000 kPa이니 해당 영역을 살펴봅시다.
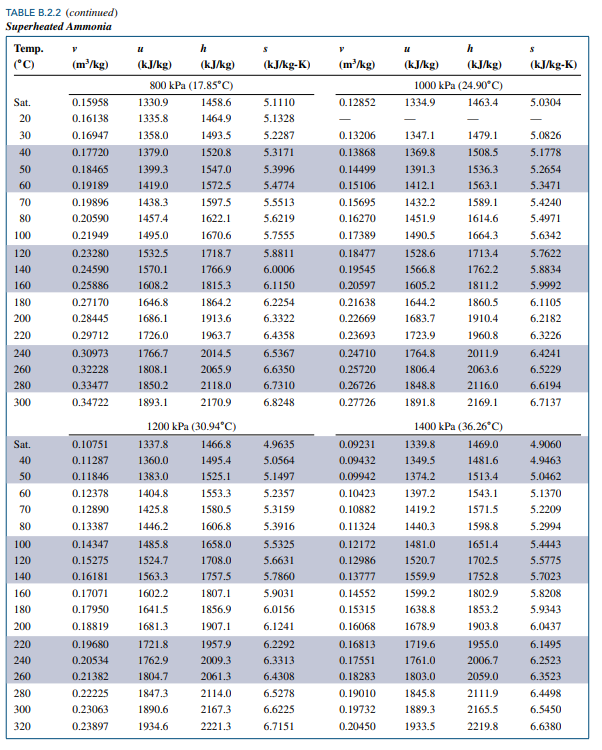
1000 kPa(24.90 C)는 1000 kPa 에서 포화온도가 섭씨 24.90도임을 의미합니다.
Saturation 일 때 물성치가 1행에 나와있고 그 아래 행들은 그 이상의 온도들에 대한 물성치입니다.
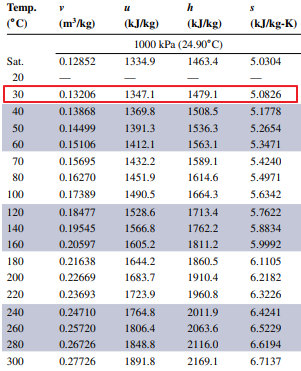
30도에서 비체적 0.13206임을 찾을 수 있습니다.
(예제 4) 10 MPa, 0.003 m^3/kg의 압력과 비체적을 가지는 물의 온도를 구하여라
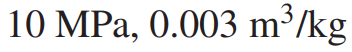
먼저 포화상태인지 확인합니다.
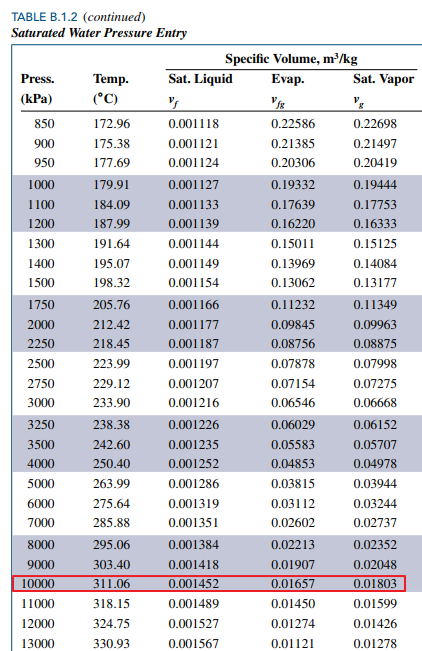
위 표로부터 vf<v<vg 임을 알 수 있습니다. 즉 포화상태라는 거죠.
따라서 물의 온도는 포화온도인 섭씨 311.06도 입니다.
(예제 5) 금속 용기에 섭씨 20도의 포화상태증기 암모니아가 담겨있다.
용기를 가열해 섭씨 40도까지 도달했을 때의 압력을 구하여라
먼저, 문제에서 암모니아가 포화상태라 하였으며 동시에 금속 용기에 담겨있다 했으니 비체적 v가 일정함을 알 수 있습니다.
이때 비체적은 20도에서의 Saturation specific volume (vg) 과 같습니다.
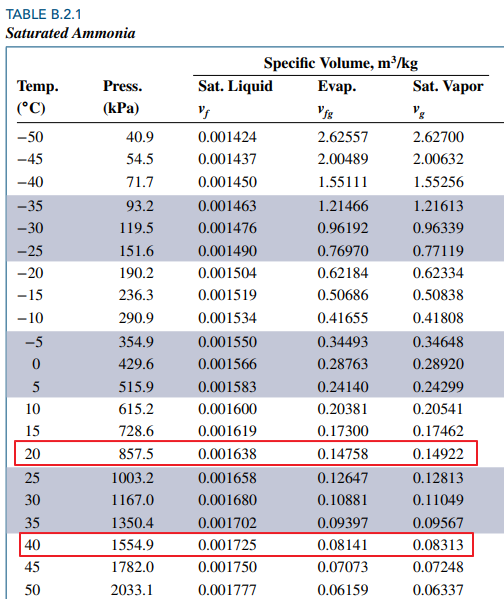
섭씨 40도에서의 비체적도 0.14922 kg/m^3 인데 이것이 섭씨 40도에서의 saturation specific volume보다 크므로 superheated vapor 라는 것을 알 수 있습니다.
superheated vapor table 를 살펴봅니다.
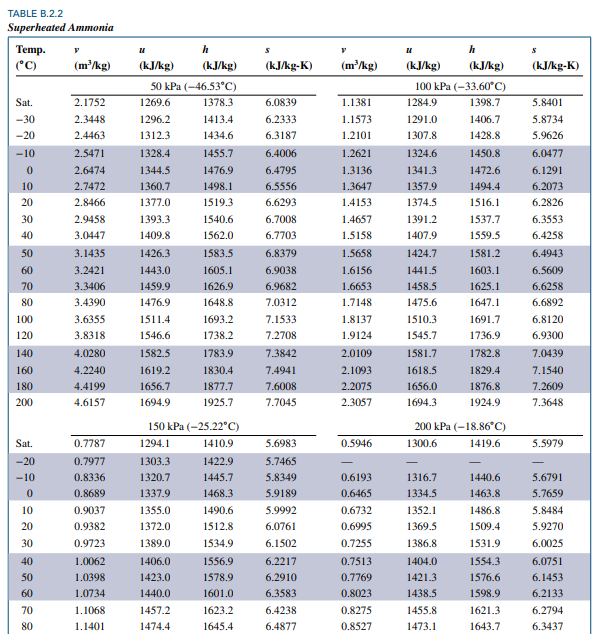
압력에 대한 정보를 모르니 섭씨 40도 행을 기준으로 v = 0.14992 에 가까운 값을 찾아야 합니다.
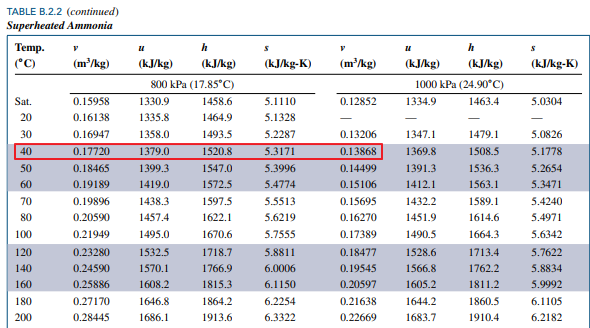
즉 압력이 800kPa 와 1000kPa 사이라는 정보를 알 수 있습니다.
800kPa < P < 1000kPa
마지막으로 선형근사를 통해 P를 구합니다.(두 물성치가 선형으로 변한다 가정)
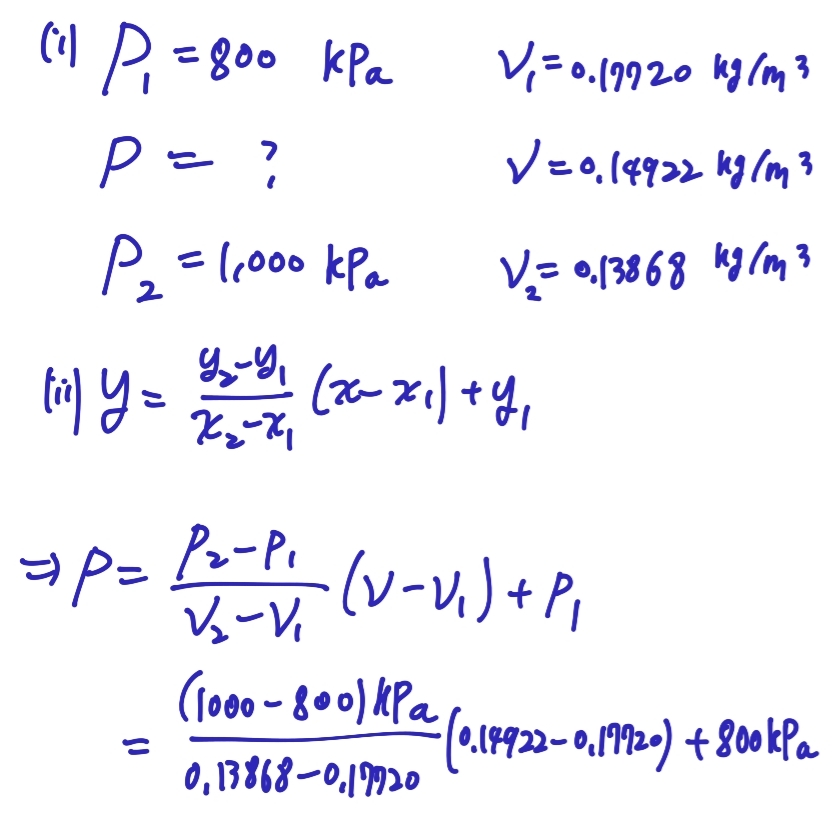
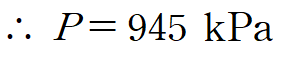
따라서 용기 내 암모니아의 압력은 945 kPa 입니다.
'기계공학 > 4대 역학' 카테고리의 다른 글
| [열역학] 압축인자 (Compressibility factor, Z) (0) | 2022.04.30 |
|---|---|
| [열역학] 이상기체 방정식 (0) | 2022.04.28 |
| [재료역학] 3. 전단력 선도와 굽힘모멘트 선도 (SFD, BMD) (1) | 2021.04.18 |
| [유체역학] 압축성 유체의 압력분포 (2) | 2021.04.14 |
| [열역학] 포화온도, 포화압력 (2) | 2021.04.11 |