재료의 변형은 공학적 설계에 있어서 주된 관심사 중 하나입니다. 주로 압축, 인장, 전단(sheer), 굽힘(bending), 비틀림(torsion) 등을 고려하여 설계하는데, 이번 글에서는 재료를 잘라 끊어지게 하는 힘인 전단력과 재료가 굽어지게 하는 굽힘모멘트에 대해서 알아보고 각각의 선도(diagram)을 알아봅시다.
※SFD는 Sheer Force Diagram, BMD는 Bending Moment Diagram 의 약자입니다.
※본 글에서는 단면적이 일정한 빔(beam)에 대한 하중만을 고려합니다.
(i) 부호 규약
먼저, 전단력과 굽힘모멘트의 부호에 관한 논의부터 시작합니다.
보(beam)에 하중이 발생하면 전단이 발생하는데 이 전단을 외부 전단과 내부 전단으로 구분합니다.
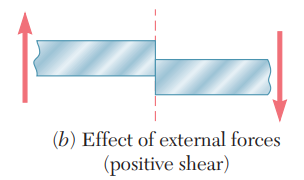
아래 그림은 외부 전단력으로, 전단이 발생하는 실제적인 방향과 같습니다. 또한 그림에서 나타나는 전단력의 방향을 양(+)의 전단력으로 정의합니다.
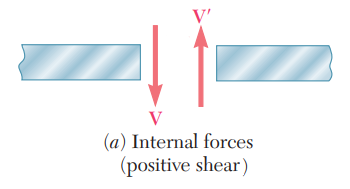
아래 그림은 내부 전단력으로, 각 지점에서 발생하는 전단력에 대해 재료 내부에서 저항하는 힘입니다. 그림에서 보는 전단력 또한 양의 전단력이지만, 외부 전단력과 방향이 반대입니다.
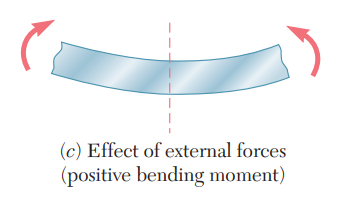
다음은 굽힘모멘트입니다. 아래 그림은 보에 실제적으로 발생하는 굽힘에 대하여 양의 굽힘모멘트를 나타낸 것입니다. 보가 아래로 튀어나오게 하는 굽힘모멘트가 양(+)의 방향 입니다. 즉 U자를 그리면 양의 방향입니다.
마찬가지로 재료 내부에서 저항하는 모멘트가 발생합니다.

이상을 양의 전단력과 양의 굽힘모멘트로 정의합니다. 어떤 방향이 양(+)의 방향인지 정의되어야 전단력 선도(SFD)와 굽힘모멘트 선도(BMD)를 그릴 때 양의 방향을 일관되게 구분할 수 있습니다.
(ii) 전단력, 굽힘모멘트와 하중의 관계
단위길이당 분포하중 w와 전단력 V의 관계는 다음과 같습니다.

전단력 V와 굽힘모멘트 M의 관계는 다음과 같습니다.

위 두 관계식의 양변을 적분하면 전단력 선도와 굽힘모멘트 선도를 그릴 수 있습니다.
첫 번째 관계식을 변수분리하고
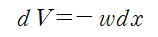
각 변수에 대해 적분해줍니다. 이때 V0은 x0에서의 전단력입니다.

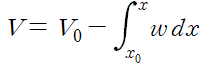
두 번째 관계식을 변수분리하고

각 변수에 대해 적분해줍니다. 이때 M0은 x0에서의 전단력입니다.
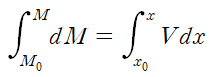
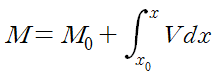
(iii) 관계식 유도
왜 위와 같은 관계식이 성립하는지, 전단력과 굽힘모멘트 관계식을 유도해봅시다.
아래와 같이 빔에 분포하중 w=f(x)이 작용합니다.
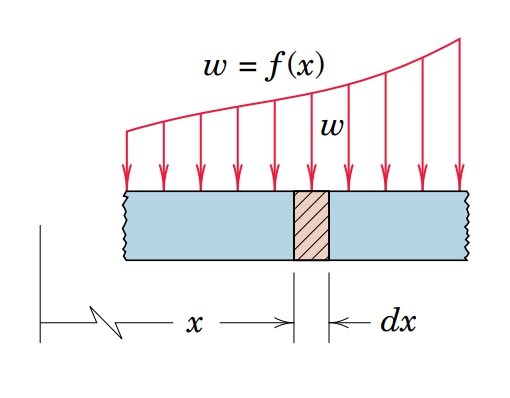
미소구간 dx에서 빔에 작용하는 힘들을 정리해 자유물체도(FBD)를 그리면 다음과 같습니다.

V와 M은 각각 x에서의 전단력과 굽힘모멘트입니다.
먼저 힘의 평형식을 적용합니다.

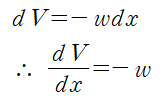
위와 같이 전단력-하중 관계식이 쉽게 유도됩니다.
다음으로는 모멘트 평형식을 적용합니다. 왼쪽면을 기준으로 모멘트 평형식을 세웁니다.


위 식에서 고차항을 날려버리면

위와 같이 미소 구간에 대한 간단한 FBD 분석으로 재료에 발생하는 전단력과 굽힘 모멘트를 유도할 수 있습니다.
(iv) 전단력 선도(SFD), 굽힘 모멘트 선도(BMD)
전단력 선도와 굽힘 모멘트 선도는 간단히, x에 대한 전단력과 굽힘 모멘트를 나타낸 그래프입니다. 즉 V=V(x)와 M=M(x)를 찾아 그리면 됩니다.
아래 그림을 봅시다. 길이가 L인 외팔보(Cantilever)에 집중하중 P가 작용하는 상황입니다.
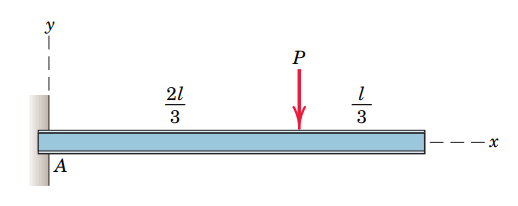
보에 작용하는 반력을 구하고, 반력을 토대로 전단력을 구하고, 전단력을 토대로 굽힘모멘트를 구하는 순서로 갑시다.
(1) 점 A에서의 반력 구하기
보에 작용하는 반력의 종류와 크기는 아래 그림과 같습니다.
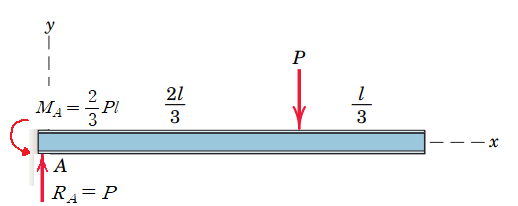
(2) 전단력 선도 구하기
아래 전단력과 하중의 관계식을 사용합니다.

먼저, x=0에서 전단력은 반력의 크기와 같으므로 V0=P입니다.

0<x< 2l/3 구간 즉 하중 P가 가해지기 전까지 구간에서는 별다른 하중이 작용하지 않기 때문에 P로 동일합니다.
x=2l/3에서 하중 P가 작용합니다.
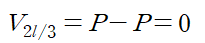
따라서 전단력 선도는 다음과 같습니다.

(3) 굽힘모멘트 선도 구하기
굽힘모멘트도 전단력과 마찬가지로 굽힘모멘트와 하중의 관계식을 사용하여 구합니다.

M0은 점 A에서 발생하는 모멘트와 같습니다. 부호규약에 따르면 아래로 튀어나오게 하는 모멘트가 양(+)이므로 M0는 음의 굽힘모멘트입니다.
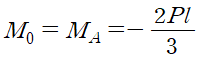
그러고는 딱히 발생하는 모멘트(여기서 모멘트는 힘에 의해 발생하는 모멘트가 아니라 순수하게 가해지는 우력)가 없으므로 전단력을 적분하여 굽힘모멘트 선도를 구합시다.

이를 종합하여 굽힘모멘트 선도를 그리면 다음과 같습니다.
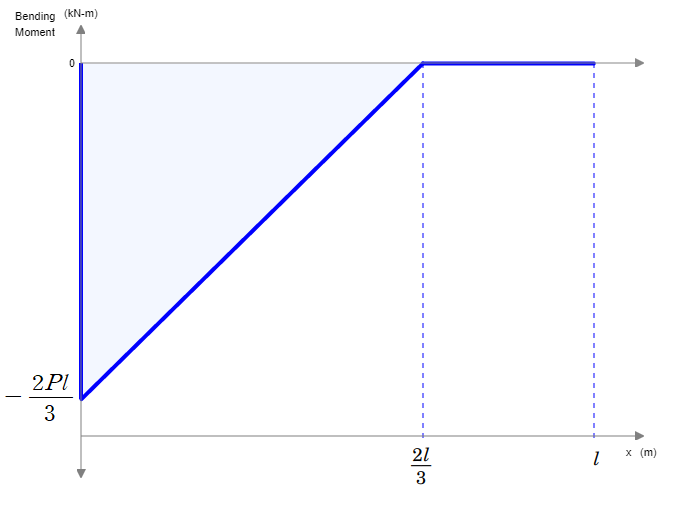
다음 글에서는 전단력 선도와 굽힘모멘트 선도를 그리는 다양한 예제를 풀어봅시다.
Any Qustions, Any Comments are WELCOME :)
오타나 오류 지적 감사히 받습니다
'기계공학 > 4대 역학' 카테고리의 다른 글
| [열역학] 이상기체 방정식 (0) | 2022.04.28 |
|---|---|
| [열역학] 순물질의 상 결정하는 방법 / 테이블에서 P,v,T 물성치 구하기 (0) | 2022.04.26 |
| [유체역학] 압축성 유체의 압력분포 (2) | 2021.04.14 |
| [열역학] 포화온도, 포화압력 (2) | 2021.04.11 |
| [재료역학] 2. 비균일 상태에서 봉의 길이변화 (0) | 2021.04.11 |