#유체역학
압력은 유체의 운동을 분석함에 있어서 매우 중요하게 고려되는 성질입니다. 한 유체 내에서 압력분포는 일정하지 않습니다. 그 예로 바다 깊은 곳에서 잠수함에 작용하는 높은 압력을 들 수 있습니다.
유체 중에서도 정지해있는 압축성 유체의 압력분포를 알아봅시다.

(i) 비압축성 유체의 압력분포
비압축성 유체의 압력분포는 아래와 같습니다.



이때 p1과 z1는 기준이 되는 지점의 압력과 높이(z)입니다.

(ii) 압축성 유체의 압력분포
먼저 유체가 압축이 용이한 기체라 가정합시다. 이상기체 방정식을 적용해 밀도를 용이하게 표현할 수 있습니다.

다들 아시겠지만 우변은 각각 기체의 밀도, 기체상수, 기체의 온도입니다.

위에서 다룬 아래 압력과 밀도 관계식에서 시작합니다.

이상기체 방정식에서 ρ를 p/RT로 치환하면 다음과 같습니다.

p를 넘기고 변수분리합니다.

양변을 각 문자에 대해 적분합니다. g와 R은 z와 관계없는 중력가속도, 기체상수 이므로 적분기호 밖으로 꺼냅니다.

이때 등온기체(온도가 기체 내 모든 지점에서 일정)일 경우 다음과 같이 T를 꺼내 적분합니다.

다음과 같이 압력 p2를 구할 수 있습니다.


기체 내에서 온도가 높이z에 따라 변할 경우 즉, T=T(z)라면 압력 p2는 다음과 같이 적분형태로 나타낼 수 있습니다.
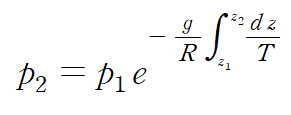

<정리>
1. 비압축성 유체의 압력분포 dp/dz = -ρg 와 이상기체 방정식 p=ρRT 로 압축성 유체의 압력분포를 유도할 수 있음
2. 온도가 기체 내에서 일정할 경우 압력분포
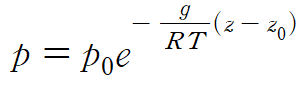
3. 온도가 기체 내에서 일정하지 않을 경우 압력분포
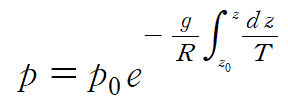
※p0은 기준높이 (z0)에서의 압력, p는 구하고자 하는 높이 (z)에서의 압력
Any Qustions, Any Comments are WELCOME :)
오타나 오류 지적 감사히 받습니다
'기계공학 > 4대 역학' 카테고리의 다른 글
| [열역학] 순물질의 상 결정하는 방법 / 테이블에서 P,v,T 물성치 구하기 (0) | 2022.04.26 |
|---|---|
| [재료역학] 3. 전단력 선도와 굽힘모멘트 선도 (SFD, BMD) (1) | 2021.04.18 |
| [열역학] 포화온도, 포화압력 (2) | 2021.04.11 |
| [재료역학] 2. 비균일 상태에서 봉의 길이변화 (0) | 2021.04.11 |
| [유체역학] 3. 공동 현상 (Cavitation) (0) | 2021.02.28 |