라그랑주 승수법에 대해 알아보고 예제를 풀어봅시다.
1. 라그랑주 승수법(Lagrange Multiplier Method)
제약조건(Constraint) 하에서 다변수함수의 최대, 최소를 구하기 위한 방법이 바로 라그랑주 승수법입니다.
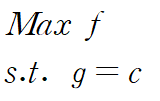
위 식은 g=c인 제약조건 하에서 f의 최댓값을 구하라는 뜻입니다. 최솟값의 경우 min으로 표시하는데 보통 위와 같은 최적화 문제를 풀 때는 임계점과 구간의 끝점에서 함숫값을 비교해 해를 구합니다. 라그랑주 승수법은 제약조건 하에서 최적화 문제를 해결하기 위한 방법으로 λ (Lagrange multiplier) 를 이용해 설정한 함수 L를 이용해 구할 수 있습니다.
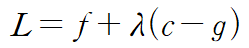
함수 L에 대해 아래 두 식을 만족하는 점이 최대 또는 최소의 후보가 됩니다.
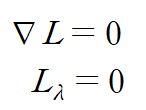
변수가 두 개인 경우
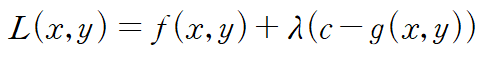
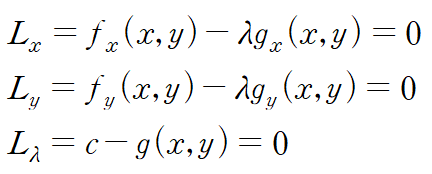
변수가 세 개인 경우
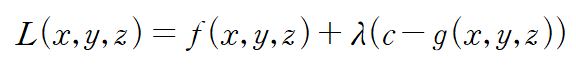
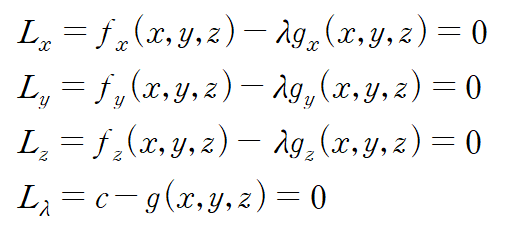
추가로 함수 L을 설정하는 것은 표현과 계산의 용이성 때문입니다. 위와 같이 설정한 함수 L은 제약조건 하에서 f와 동일한 값을 가지는 함수가 됩니다.
2. 예제
(예제 1) 타원 C 상에서 f(x,y)의 최대, 최소를 구하여라
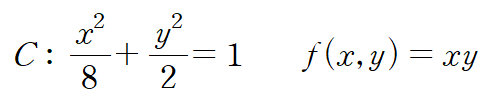
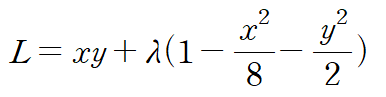
L을 x와 y에 대해 미분합니다. 아래는 L의 임계점을 구하는 과정입니다.
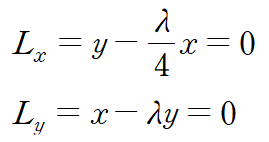
위 두 식으로부터 연립방정식을 얻습니다.
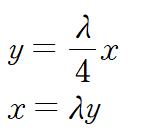
해를 구하면 x와 y 모두 0이거나 λ=±2 입니다.

(x,y)=(0,0) 이라는 임계점후보를 하나 구했습니다. λ=±2 으로부터 얻어지는 임계점도 확인해봅시다.
g(x,y)=c 에 x=λy 를 대입합니다.
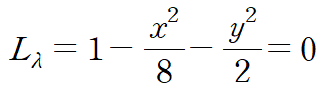
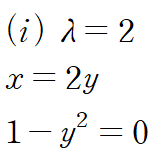
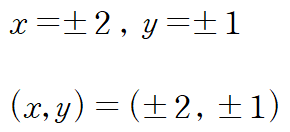
두 개의 임계점을 구했습니다.
마찬가지로 λ=-2 에 대한 두 임계점을 찾을 수 있습니다.
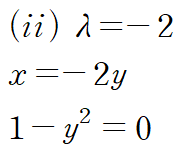
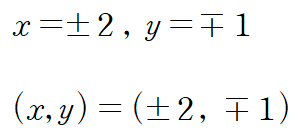
그런데 (0,0)은 제약조건 g(x,y)=c 를 만족시키지 않으므로
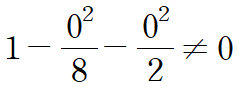
임계점 후보는 다음 네 점입니다.
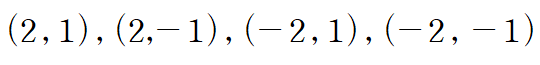
각 임계점에서 f(x,y)를 구합니다.
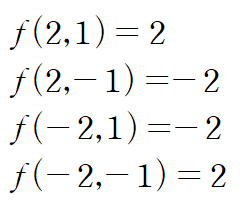
이것이 최대, 최소의 후보가 됩니다.
따라서 타원 C에서 f의 최댓값은 2, 최솟값은 -2입니다.
(예제 2) g(x,y)=2x+3y-6=0 위의 점 중 원점으로부터의 최단거리를 구하여라
목적함수(최적화의 대상이 되는 함수)를 설정하면 다음과 같습니다.
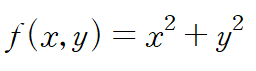
루트를 씌워도 되지만 계산의 편의성을 위해 "거리의 제곱"을 f(x,y)로 잡습니다.
함수 L은 다음과 같이 설정할 수 있습니다.
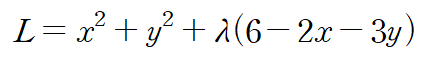
임계점을 구합니다.

임계점은 아래와 같습니다.
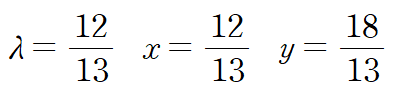
임계점에서 목적함수의 함숫값은 아래와 같습니다.
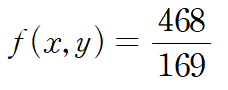
목적함수는 거리의 제곱이었으니 함숫값에 루트를 씌워주면 최단거리를 구할 수 있습니다.
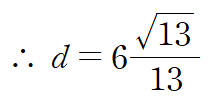
(예제 3) (x,y,z) 공간 상에서 중심이 원점이고 반지름이 3인 구에 대해 x+y+2z의 최대, 최소를 구하여라
함수 L을 설정하면 다음과 같습니다.
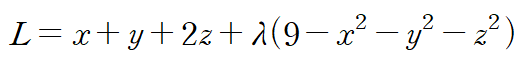
각 문자에 대한 편도함수로부터 임계점을 구합니다.

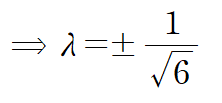
이상의 결과로부터 임계점은 다음과 같습니다.
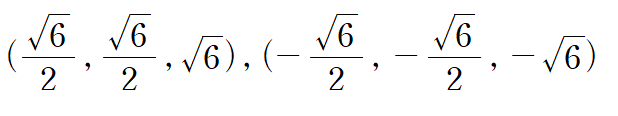
따라서 x+y+2z 의 최대, 최소는 다음과 같습니다.
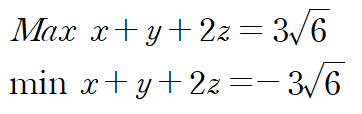
ㄴ
(예제 4) 평면 α 와 원추 G는 한 곡선에서 만난다. 원점에서 가장 가까운 곡선 위의 점을 구하여라
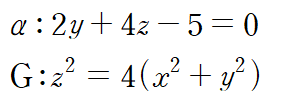
곡선을 직접 구해서 하나의 제약조건으로 만들어도 되고, 두 개의 제약조건을 사용해도 좋습니다. 저는 두 개의 제약조건으로 취급하였는데 하나의 제약조건으로 만들 때는 y = 2.5-2z 를 G에 대입하면 됩니다.
두 번째 예제처럼 거리의 제곱을 목적함수로 설정합니다.
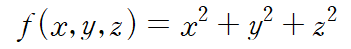
함수 L을 설정합니다. 이때 각각 다른 라그랑주 승수를 사용해 표현합니다.
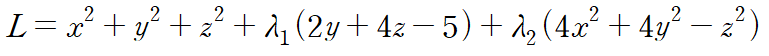
편도함수들로부터 방정식을 얻으면 아래와 같습니다.
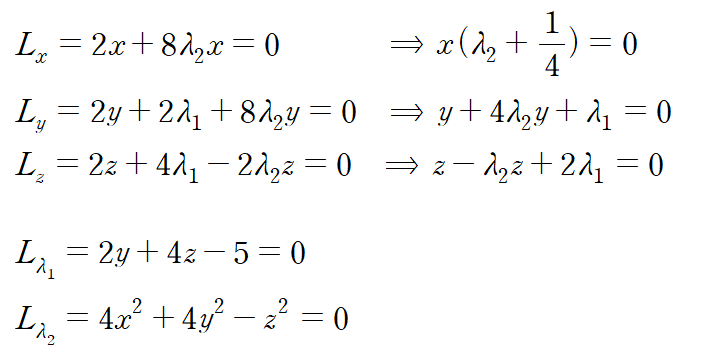
Lx 로부터 몇 가지 경우를 나눌 수 있습니다. 첫 번째 경우부터 따져봅시다.
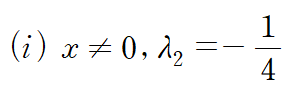

x,y,z를 모두 구했는데 이것이 마지막 방정식을 만족시키지 못합니다.
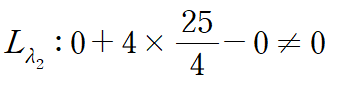
첫 번째 경우가 모순이므로 x=0입니다.
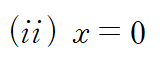
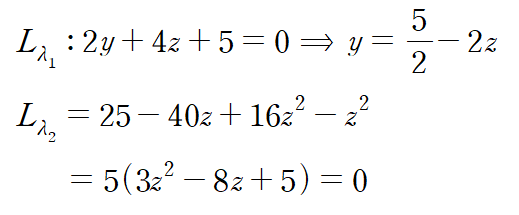
z를 구하면 아래와 같고 각각의 z에 대응하는 y도 구할 수 있습니다.
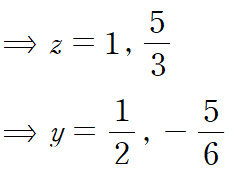
따라서 임계점은 아래 두 점입니다.
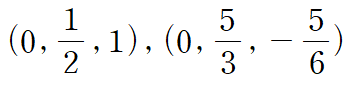
각각의 임계점에서 나머지 편도함수가 모두 0인지 확인해보아야 하지만 여기에 적지는 않겠습니다.
각각의 임계점에 대해 편도함수를 0으로 만드는 λ1, λ2 가 존재하므로 이로써 모든 조건을 만족시킵니다.
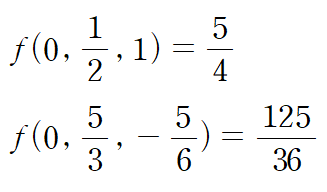
따라서 원점과 가장 가까운 곡선 위의 점은 (0, 1/2, 1) 입니다.
'MATHEMATICS > 미분적분학' 카테고리의 다른 글
| [미분적분학] 방향도함수 (Directional Derivative) (0) | 2022.07.28 |
|---|---|
| [미분적분학] 그린정리(Green's Theorem) 예제 (0) | 2021.12.23 |
| [미분적분학] 그린정리(Green's Theorem) 예제 (0) | 2021.12.10 |
| [미분적분학] 다변수함수의 편미분, 연쇄법칙 (Chain Rule) (2) | 2021.11.08 |
| [미분적분학] Cylindrical Shell Method (4) | 2021.04.17 |