#선형대수학
1. 특성방정식 (Characteristic Equation)
특성다항식(Characteristic Polynomial)이라고도 하는데, 행렬의 고윳값을 구하기 위한 도구입니다

위 식을 특성방정식이라 부르는데, 유도 과정은 다음과 같습니다
3 x 3 행렬 A를 봅시다
고윳값 λ가 존재한다면 다음 등식에서 0이 아닌 해 x가 존재합니다

이때 우변에 존재하는 고윳값과 항등행렬(Identity matrix)의 곱을 생각해봅시다

고윳값 λ와 x 사이에 항등행렬을 끼워넣어 계산하면 우변은 다음과 같습니다

즉 다음과 같이 표현할 수 있구요
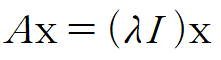
좌변으로 몰아 정리합니다

고윳값과 고유벡터의 정의에 의해 위 등식에서 영벡터가 아닌 해(nontrivial solution, 자명하지 않은 해)가 존재해야 합니다. 어떤 행렬에 대해 Ax=0 자명하지 않은 해가 존재한다면 행렬 A은 역행렬이 존재하지 않습니다. 즉 행렬식 det A = 0 입니다
따라서 좌변의 행렬식이 0입니다

3 x 3을 예시로 들었는데 n x n 도 동일합니다
2. 특성방정식으로 고윳값 구하기
다음 2 x 2 행렬 A의 고윳값을 구해봅시다

A-λI의 행렬식을 계산합니다

2 x 2 행렬의 determinant는 다음 공식으로 쉽게 구할 수 있습니다

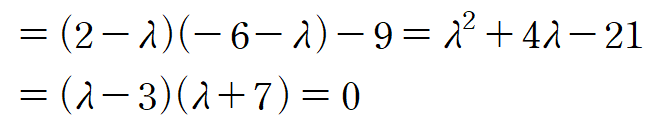

위와 같이 2 x 2 행렬의 고윳값은 λ에 대한 이차방정식의 해를 구하는 것과 같구요, 3 x 3 행렬은 삼차방정식, n x n 행렬의 경우 n차방정식의 해를 구하는 것과 같습니다
(예제 1) 행렬 A의 고윳값을 구하여라
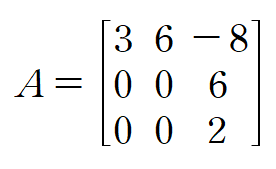
A-λI의 행렬식을 세우고 계산해주면 됩니다
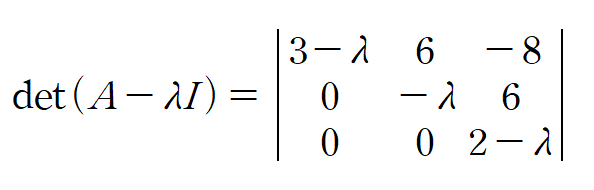

따라서 A의 고윳값은 0, 2, 3 입니다
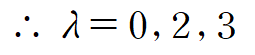
고윳값이 0이 나왔는데 이것의 의미는
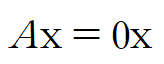
위 방정식의 0이 아닌 해가 존재, 즉
Ax=0의 0이 아닌 해가 존재한다는 뜻이며

A의 역행렬이 존재하지 않는다는 것을 내포합니다(또한 det A=0)
3. 특성방정식으로 고유벡터 구하기
고윳값을 구했으니 이번에는 고유벡터를 구해봅시다
간단히 (A-λI)x=0의 해를 구하면 그것이 곧 고유벡터가 됩니다
위에서 봤던 2 x 2 행렬을 다시 봅시다
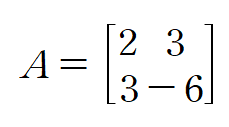
고윳값이 3,-7이었는데 각 고윳값에 대응되는 고유벡터를 찾아봅시다
(예제 2) A의 한 고윳값 3에 대응되는 한 고유벡터를 구하여라
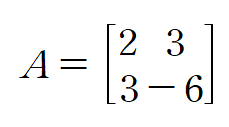
(A-3I)x의 해를 구하기 위해 다음과 같이 첨가행렬을 세웁니다
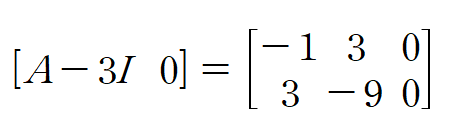
기초 행연산(Elementary row operation)을 통해 해를 구합니다
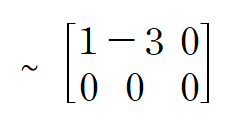
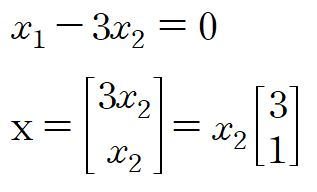
위 x가 고윳값 3에 대한 A의 고유공간이 되며 적당한 상수를 x2에 대입해 고유벡터를 구할 수 있습니다
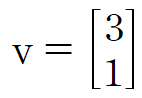
3에 대한 A의 한 고유벡터
(예제 3) 행렬 B의 고윳값과 각 고윳값에 대응되는 고유벡터를 구하여라
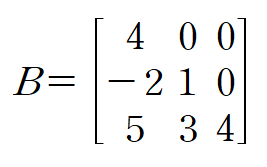
먼저 특성방정식을 적용해 고윳값을 구합니다


위와 같이 중복되는 만큼 고윳값 4를 적어도 되고 간단히 1, 4라고 구해도 상관 없습니다. 일반적으로 n x n 행렬의 고윳값이 n개이기 때문에 위와 같이 표현합니다
고윳값 1에 대한 고유벡터를 구해봅시다
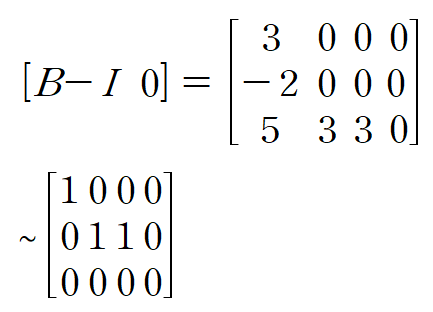
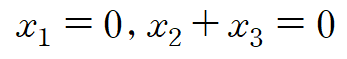
해집합이 다음과 같이 표현되므로
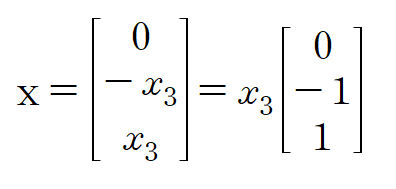
고윳값 1에 대한 행렬 A의 고유벡터는 (0,1,1) 입니다
다음은 고윳값 4에 대한 고유벡터입니다
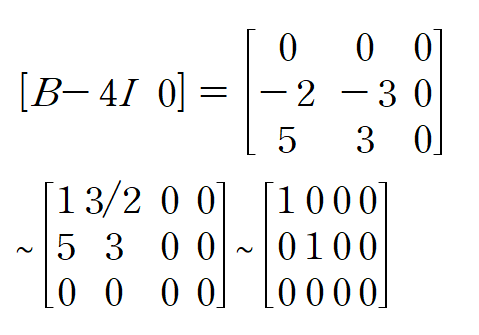
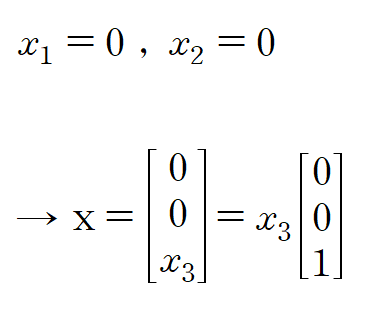
고윳값 4에 대한 행렬 A의 고유벡터는 (0,0,1)입니다
Any Qustions, Any Comments are WELCOME :)
오타나 오류 지적 감사히 받습니다
'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| [선형대수학] 그람-슈미트 과정 (Gram-Schmidt Process) 예제 (0) | 2021.12.21 |
|---|---|
| [선형대수학] 크래머 공식 (Cramer's Rule) (0) | 2021.11.18 |
| [선형대수학] 고윳값, 고유벡터, 고유공간 (Eigenvalue, Eigenvector, Eigenspace) (0) | 2021.11.10 |
| [선형대수학] 크래머 공식 (Cramer's Rule) (0) | 2021.11.04 |
| [선형대수학] 열공간과 영공간 (Column Space and Null Space) (7) | 2021.11.01 |