1. 차원의 정의 (Definition of Dimension)
차원(dim)의 정의는 다음과 같다
부분공간 H에 대해 H의 기저의 원소의 개수를 Dimension of H (dim H)라 한다
예를 들어 basis for H = {b1, b2} (부분공간 H의 기저가 2개} 이면 dim H = 2 이다
정의에 더불어 두 가지 알아야 할 성질(property)이 있다
a. 부분공간 H의 기저에 대해 기저들의 집합 B의 원소의 개수(벡터의 개수)는 항상 일정하다(dim H = 일정)
b. H ={0}일 때 즉, 부분공간 H가 영벡터일 때, dim {0} = 0 으로 정의된다 ({0}은 선형종속이기 때문에 기저가 될 수 없다)
간단히 dim H = H의 기저 개수
(예제 1) 행렬 A에 대해 dim(Nul A)를 구하여라

이전 글에서 영공간 예제에 나온 행렬과 동일합니다

REF를 구했으니 일반해(General solution)를 구해봅시다


Nul A의 기저는 다음과 같습니다

Nul A의 기저의 원소가 2개이니 dim(Nul A)=2입니다
중요한 정리를 하나 보고 Col A의 차원을 구해봅시다
> 영공간의 차원은 Ax=0의 자유변수(Free variable)의 개수이고, 열공간의 차원은 A의 피벗 칼럼의 개수이다
영어 원문) The dimension of Nul A is the number of free variables in the equation Ax = 0, and the dimension of Col A is the number of pivot columns in A
(예제 2) 행렬 A에 대해 dim(Col A)를 구하여라

Col A의 차원계산은 A의 Echelon form을 구하는 것부터 시작합니다
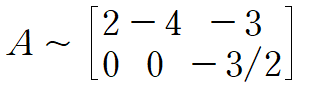
첫 번째, 세 번째 열이 pivot column이므로 두 개의 기저를 가지며 따라서 dim(Col A) = 2 입니다
2. 랭크의 정의 (Difinition of Rank)
랭크는 행렬과 관계가 있습니다. 즉 행렬의 중요한 성질 중 하나라는 거죠
랭크의 정의는 다음과 같습니다
행렬 A의 랭크는 rank A 라 표기하며 A의 열공간의 차원의 개수 즉 rank A = dim(Col A)이다
영어 원문) The rank of a matrix A, denoted by rank A, is the dimension of the column space of A.
방금 살펴본 예제에서 알 수 있듯이 Col A의 차원은 A의 피벗 칼럼의 개수와 같다
> The rank of A is just the number of pivot columns in A because the pivot columns of A form a basis for Col A
3. 랭크 정리 (Rank Theorem)
이 정리는 너무나 자명하기 때문에 별다른 증명 없이 사용합니다
행렬 A가 n개의 열을 가지면 Rank A + dim(Nul A) = n 이다
A를 echelon form으로 변환하면 A의 행렬을 pivot column과 pivot이 없는 column으로 나눌 수 있습니다. 이때 pivot column의 개수는 dim(Col A) 즉 Rank A가 되며 pivot이 없는 column은 Ax=0의 해에서 free variable로 취급할 수 있으며 그 개수가 dim(Nul A)와 같습니다. 따라서 Rank A + dim(Nul A) 가 행렬 A의 열 크기 n과 같게 되며 따라서 Rank A + dim(Nul A) = n이 성립합니다
Any Qustions, Any Comments are WELCOME :)
오타나 오류 지적 감사히 받습니다
'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| [선형대수학] 열공간과 영공간 (Column Space and Null Space) (7) | 2021.11.01 |
|---|---|
| [선형대수학] 부분공간, 기저 (Subspace, Basis) (0) | 2021.10.30 |
| [선형대수학] 열공간과 영공간 (0) | 2021.10.27 |
| [선형대수학] 선형방정식 (2) (0) | 2021.10.19 |
| [선형대수학] 선형방정식 (1) (0) | 2021.10.18 |