#선형대수학
앞선 글)
https://subprofessor.tistory.com/46
1. 선형방정식계를 푸는 법 (Solving a linear system)
Elementary Row Operations (약어로 ERO, 한글로는 기본 행 연산이라고 번역?) 을 이용해 선형방정식의 해를 구할 수 있습니다. ERO는 다음 세 가지 연산을 의미합니다

직접 선형방정식계의 해를 구해보며 ERO를 익혀봅시다

주어진 선형방정식계로부터 첨가행렬(augmented matrix)을 세우면 다음과 같습니다

이때 첫 번째 행을 R1, 두 번째 행을 R2 이라 표기합시다

먼저 R2와 R1을 더해 새로운 R1을 만듭니다

우변의 R1는 좌변의 R1과 다른데, replacement라는 이름에서 알 수 있듯이 행 자체를 앞선 연산을 통해 대체하는 것입니다. 해서 R1가 [3 0 6]으로 대체되었죠?
다음으로는 R1을 3으로 나누어 간단하게 만듭니다

1/3 R1 -> R1 식은 "첫 번째 행에 1/3을 곱한 것을 새로운 첫 번째 행 R1으로 합니다" 를 의미해요
다음으로는 두 번째 행을 다듬어 줍시다

여기까지 보시면 통상적으로 replacement를 수행할 때 좌변의 두 번째 항과 우변의 항이 같음을 알 수 있습니다
scaling을 두 번째 행에 수행해주면

다음과 같은 해를 얻습니다(첨가행렬에서 다시 변환)

한 행에서 각 변수들의 자리에 1만 남기도록 ERO를 수행해주면 되는데, 이러한 형태를 echelon form(사다리꼴 행렬) 이라 부릅니다. 그러니까 궁극적으로 이 echelon form을 만들기 위해 ERO를 수행한다는 거죠. 이 형태로 만들어야만 선형방정식계의 해를 구할 수 있습니다(현 단계에서는)
2. Row equivalent and two fundamental questions about a linear system
두 행렬이 다음 조건을 만족할 때 Row equivalent(행 상등)이라 합니다
"한 첨가행렬이 ERO를 통해 다른 선형방정식계와 같은 형태로 만들어지면 Row equivalent"
또한 두 행렬이 Row equivalent 이면 동일한 해를 가진다
(영어 원문) If the augmented matrices of two linear systems are row equivalent, then the two systems have the same solution set
선형대수학에서는 두 가지 질문에 포커싱하는데 바로 해의 존재성과 유일성입니다
Q1. 시스템의 해가 적어도 한 개 존재하는가? (existence)
Q2. 만약 해가 존재한다면 유일한 해인가? (uniqueness)
특히 유일하다는 것에서 파생되는 개념이 많으니 이후에도 주의깊게 봐줍시다
3. 사다리꼴 행렬 (Echelon form)
저희 교수님이 '엣쉴론 폼'이라고 발음하셨던 기억이 나네요
(1) Leading entry : 한 행에서 0이 아닌 항들 중, 가장 왼쪽 column에 속하는 항
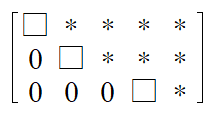
위 행렬에서 □가 바로 leading entry가 됩니다. Leading entry는 열(column, 세로줄)을 기준으로 셉니다
(2) Echelon form : 다음 세 조건을 만족하면 그 행렬의 형태를 echelon form이라 합니다

1번 조건은 말 그대로 [0 0 0 . . . 0] 항이 행렬의 맨 아래에 위치해야 한다는 뜻
2, 3번 조건은 아래 행렬처럼 위치해야 한다는 것입니다. 두 번째 열의 leading entry를 보면 그 위는 뭐가 와도 상관없고 아래가 0이라는 걸 볼 수 있습니다
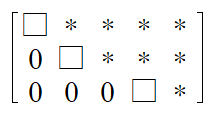
추가적으로 echelon form과 leading entry가 모든 행에 존재하는 것과는 관련이 없습니다. 위 행렬의 경우 세 번째 열에 leading entry가 없지만 echelon form으로 분류됩니다
(3) Reduced echelon form : echelon form의 세 조건에 더해 추가적인 두 조건을 만족하면 reduced echelon form이라 합니다

reduced echelon form 형태로 만들어야 선형방정식계의 해를 구할 수 있습니다
4번 조건은 위 echelon form에서 leading entry(네모, □)가 1이어야 한다는 것입니다
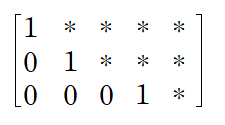
5번 조건을 적용하면 아래와 같습니다
ERO가 선형방정식 계의 해를 구하는 도구라고 했는데, 그 해를 구하는 과정의 종착지가 바로 이 Reduced echelon form입니다.(REF) REF 형태로 만든다는 것이 곧 해를 구한다는 것을 의미합니다. 처음 예시로 든 선형방정식계의 해와 비교해보면 무슨 말인지 알 수 있습니다. ERO의 방향을 먼저는 echelon form을 구하는 것, 그 다음으로 reduced echelon form으로 만드는 것으로 잡아야 한다는 말이죠
4. Pivot positions, pivot columns
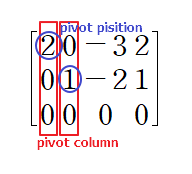
피벗 포지션의 개념은 echelon form에서의 leading entry와 같습니다
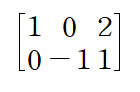
위 첨가행렬에서 leading entry는 첫 번째 열에서 1, 두 번째 열에서 -1 입니다(echelon form의 경우 leading entry가 1일 필요는 없습니다)
pivot position은 leading entry의 위치 라고 이해하시면 되구요 나아가 pivot column은 이 pivot position이 속한 column을 의미합니다
5. 선형방정식 계의 해
해를 구하는 구체적인 방법을 알았으니 해의 형태(종류)에 관해 더 자세히 들어가봅시다
일반적으로 고등학교에서는 연립방정식을 풀기 위해서 문자의 개수만큼 서로 다른 식이 필요하다고 하지요? 이 단원에서는 REF(Reduced echelon form)의 형태를 보고 해의 형태를 판단할 수 있습니다. 유일한 해인지, 무수히 많은 해인지 판별할 수 있다는 말이죠
먼저, 해를 구하기 전에 주어진 선형방정식으로부터 얻은 계수행렬의 REF를 얻어야 합니다
그 다음 pivot position을 보고 두 가지 경우로 나누어 생각합니다

아래 행렬은 계수행렬에 몇 차례 ERO를 시행해 얻은 REF입니다
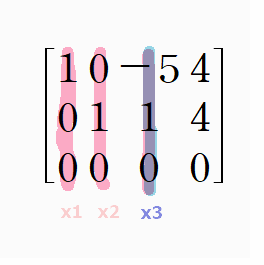
각 열(세로줄)이 변수들을 의미하는데 세 번째 줄만 pivot이 없습니다. 해서 x3는 free variable이 됩니다. 나머지 x1, x2는 pivot position을 가지므로 basic variable 이구요
basic variable은 free variable을 통해 표현됩니다
REF 꼴인 첨가행렬을 다시 변수들을 사용해 나타내면 아래와 같습니다
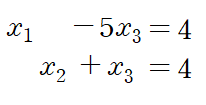
여기서 free variable로 basic variable을 표현합니다
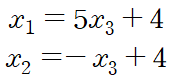
x3이 free variable이라고 불리는 것은 고정된 값이 없다는 뜻이며 예시로 든 선형방정식계는 무수히 많은 해를 가집니다. 통상적으로 REF에서 [0 0 0 . . . 0] 행이 있으면 free variable이 존재한다는 뜻이고 무수히 많은 해를 가집니다. 해서 유일한 해를 가지기 위해서는 변수의 개수만큼 pivot position이 존재해야만 합니다
이번에는 해의 존재성에 대해 살펴봅시다
아래는 선형방정식계를 REF로 변환해 해를 구하는 과정입니다
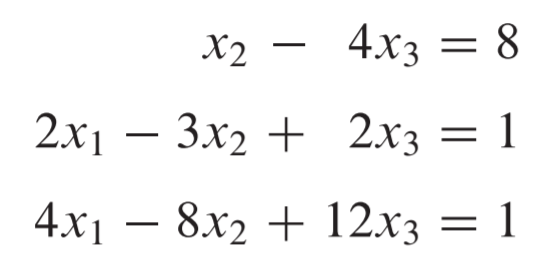
첨가행렬을 얻고
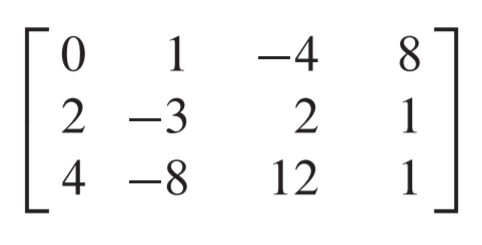
Echelon form이 되도록 적절히 ERO를 수행합니다
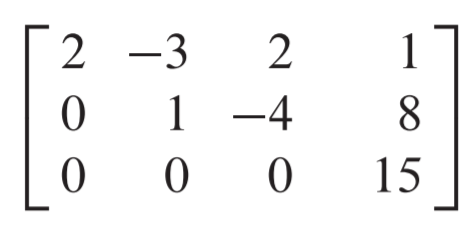
이때 세 번째 행이 [0 0 0 15]가 되었는데 이는 0 = 15라는 의미죠? 따라서 모순이며 이 경우 해가 존재하지 않습니다. 여기서 해의 존재성에 관한 정리가 등장합니다
[0 , , , 0 b] (b ≠ 0) 인 row가 있으면 선형방정식계가 inconsistent, 즉 해를 갖지 않는다.
(A linear system is consistent if and only if the rightmost column of the augmented matrix is not a pivot column—that is, if and only if an echelon form of the augmented matrix has no row of the form [ 0 , , , 0 b ] with b nonzero)
free variable을 통한 해의 유일성에 관한 정리는 다음과 같습니다
선형방정식계는 free variable이 없으면 유일한 해를, free variable이 있으면 무수히 많은 해를 가진다.
(If a linear system is consistent, then the solution set contains either (i) a unique solution, when there are no free variables, or (ii) infinitely many solutions, when there is at least one free variable)
선형방정식의 해를 구하는 예제풀이는 다음 글에서 알아봅시다
※2024-1 선형대수학 연립방정식 파트 모의고사 2회분 판매중입니다(3,900원)※

☕ 커피 한 잔보다 싼 선형대수학 모의고사 ☕
✅ 선형대수학 연립 일차 방정식 단원 모의고사 2회분입니다.
✅ 문제는 영어, 해설은 한국어입니다.
✅ 회당 10문제, 상세한 해설 포함 (12p가량)
🚫 본 모의고사는 시험 대비 및 복습용으로 제작되었습니다.
🚫 모든 문제의 저작권은 섭교수 연구소에 있으며 자료의 무단 배포 및 판매를 금지합니다.
🚫 전자책 특성 상 환불이 불가합니다.
✉️ 질문 및 기타 문의는 hyonklee@gmail.com
시험지 샘플입니다.


해설 샘플입니다.

Any Qustions, Any Comments are WELCOME :)
오타나 오류 지적 감사히 받습니다
'MATHEMATICS > 선형대수학' 카테고리의 다른 글
| [선형대수학] 열공간과 영공간 (Column Space and Null Space) (7) | 2021.11.01 |
|---|---|
| [선형대수학] 부분공간, 기저 (Subspace, Basis) (0) | 2021.10.30 |
| [선형대수학] 차원, 랭크 (Dimension, Rank) (0) | 2021.10.29 |
| [선형대수학] 열공간과 영공간 (0) | 2021.10.27 |
| [선형대수학] 선형방정식 (1) (0) | 2021.10.18 |