#수치해석
반복법(Iterative Methods)은 연립방정식을 풀기 위한 방법의 일종으로 행렬연산이나 가우스 소거법과는 다른 방식으로 해를 구합니다.
이 게시글은 두 가지 반복법 가우스-자이델 방법(Gauss-Seidel Method)과 야코비 반복법(Jacobi Iteration)을 소개합니다.
1. Gauss-Seidel Method
아래와 같이 행렬로 표현된 연립방정식이 있습니다.
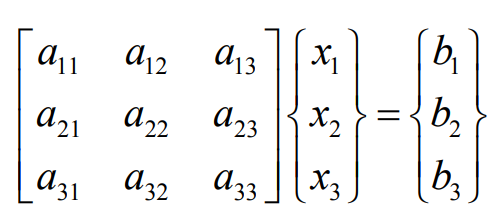
각 행이 의미하는 바는 다음과 같습니다.
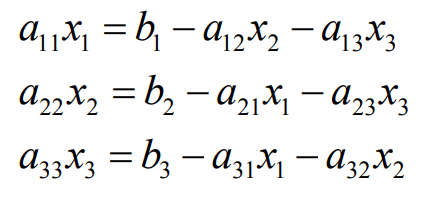
위 식에서 각각 x1, x2, x3에 대해정리하면 다음과 같습니다.
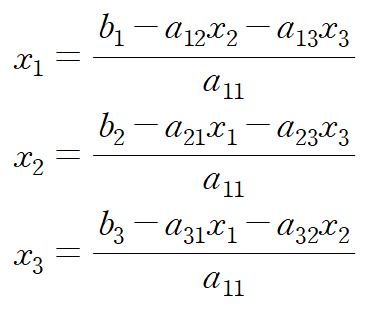
가우스-자이델 방법은 위 식들의 우변에 각각 "직전 단계에서 업데이트된 x1, x2, x3"를 대입하는 것입니다.
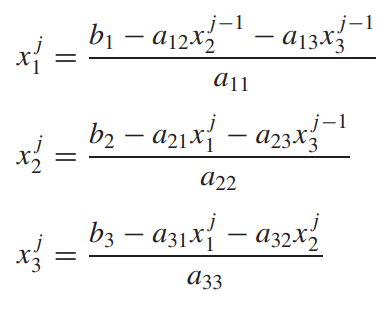
(예제 1) 가우스-자이델 방법을 사용하여 연립방정식의 해를 구하여라
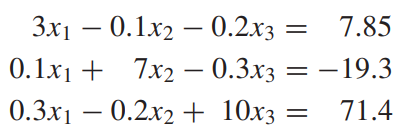
먼저, 각 행으로부터 x1, x2, x3를 각각 다른 두 미지수로 표현합니다.
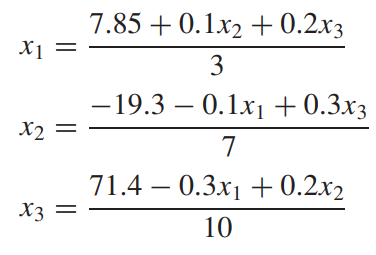
초깃값을 가정해야 하는데 여기서는 (0,0,0)으로 하겠습니다.
이것을 첫 번째 식에 대입합니다.
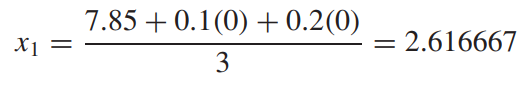
이후 두 번째 식에 대입할 건데, 이전 단계에서 업데이트된 x1을 사용합니다.

마찬가지로 세 번째 식에 대입할 때에도 이전 단계에서 업데이트된 x2를 사용합니다.(x1은 전전단계에서 업데이트 되었음)
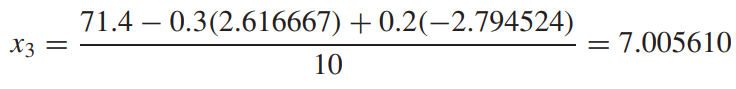
이 세 번의 대입을 한 사이클이라고 합시다.
이것을 한 번 더 반복하면 다음과 같습니다.

이런 식으로 대입하는 것을 일정 오차 이하로 수렴할 때까지 반복하여 수치해를 구하는 방법을 가우스-자이델 방법이라고 합니다.
2. Jacobi Iteration
야코비 반복법도 유사한 방법을 사용하나, 업데이트를 한 사이클이 끝난 이후에 한 번에 한다는 차이점이 있습니다.
(예제 2) 야코비 반복법을 사용하여 연립방정식의 해를 구하여라
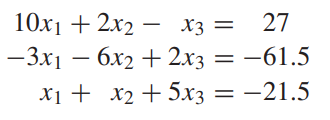
가우스-자이델 방법에서 했던 것처럼 x1, x2, x3에 대해 각 행을 정리합니다.
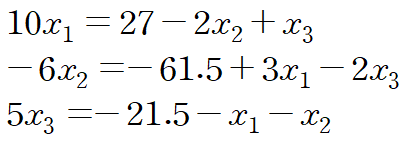
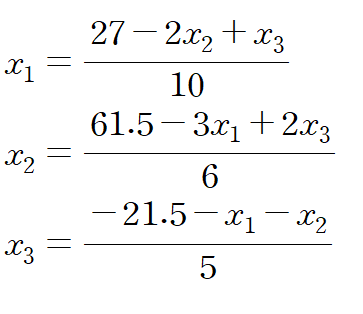
다음으로는 초깃값을 대입합니다. 여기서는 (0,0,0)을 사용해보겠습니다.
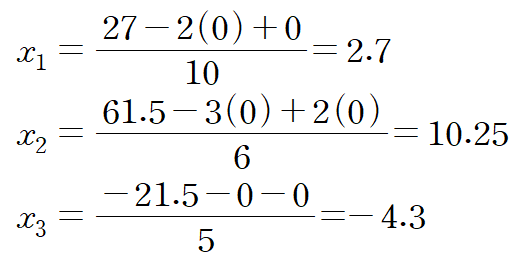
한 번 반복한 후의 결과는 (2.7, 10.25, -4.3)입니다.
이것을 다시 한꺼번에 대입합니다.
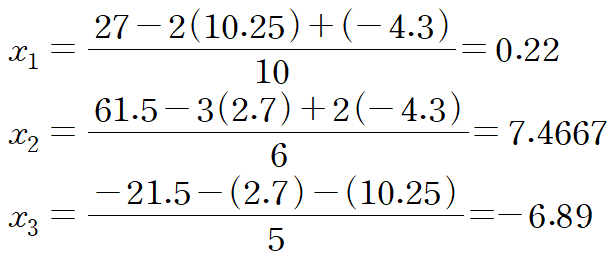
다시 한꺼번에 대입합니다.

이처럼 한꺼번에 업데이트하며 연산을 반복해 수렴하는 해를 구하는 것이 야코비 반복법입니다.
3. Convergence and Row Interchange
이러한 반복법은 행렬의 크기가 클수록 가우스 소거법보다 더 좋은 효율을 발휘합니다.
하지만 항상 반복법을 통한 해가 수렴하는 것은 아닙니다.
"Diagonal Dominance"라는 조건을 만족해야 반복법이 수렴합니다.
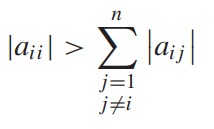
즉 대각성분의 절댓값이 같은 행의 다른 성분들의 절댓값의 합보다 커야 수렴성이 보장된다는 것입니다.
앞선 예제들은 모두 이 Diagonal Dominance를 만족하는 경우였으며
혹 만족하지 않는다면 행의 위치를 바꾸는 Row Interchange 연산을 통해 만족하도록 바꾼 후 반복법을 진행하면 됩니다.
* 위 관계식에서 등호인 경우에는 수렴할 수도 있고 수렴하지 않을 수도 있습니다.
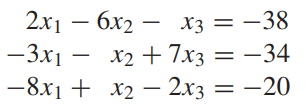
위와 같은 경우에는 다음과 같이 행연산을 수행한 후 반복법을 진행합니다.
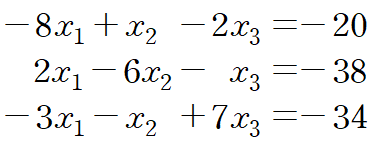
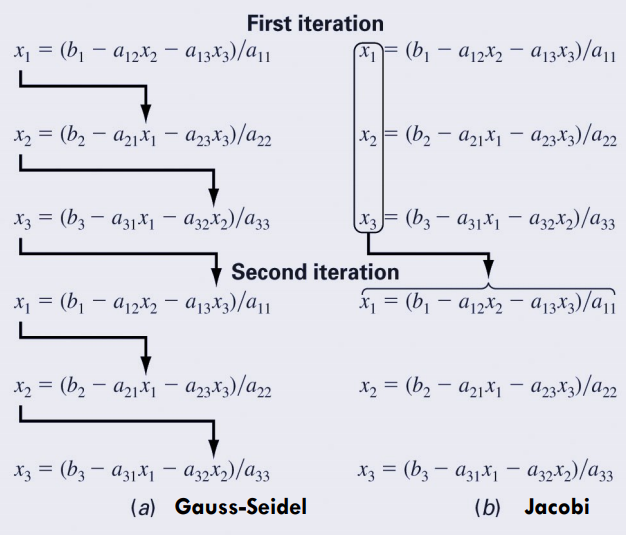
아래는 가우스-자이델 방법(a) 과 야코비 반복법(b)의 메커니즘을 간단히 정리한 그림입니다.
'MATHEMATICS > 수치해석학' 카테고리의 다른 글
| [수치해석] 다항회귀 예제(Polynomial Regression), 매트랩 코드 (0) | 2023.07.29 |
|---|---|
| [수치해석] 비선형 회귀(Nonlinear Regression) 예제, 매트랩 코드 (0) | 2023.07.27 |
| [수치해석] 룽게-쿠타 방법(Runge-Kutta Method), 룽게 쿠타 4차 예제 (0) | 2023.06.08 |
| [수치해석학] LU분해(LU Factorization), 파이썬 코드 (1) | 2023.01.26 |
| [수치해석학] 뉴턴-코츠 공식, 심슨 룰(Newton-Cotes Formula, Simpson's Rule) (1) | 2021.12.25 |