0. Introduction
비선형 회귀에 대한 예제를 풀어보기 이전에 간단히 선형 회귀에 대해 설명하겠습니다.
선형 회귀(Linear Regression)이란 주어진 (x,y) 데이터에 대해 에러의 제곱합을 최소화하는 직선을 찾는 것입니다.
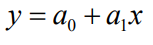
위와 같은 직선을 구성하는 요소는 기울기 a1과 y절편에 해당하는 a0 두 가지입니다.
에러의 제곱합은 아래와 같이 표현되며 앞서 말했듯 이것이 최소가 되도록 하는 직선, 즉 a1과 a0를 찾으면 됩니다.
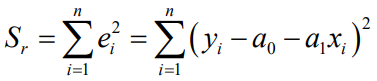
어떠한 변수에 대해 최소가 되는 지점은 "미분"을 통해 알 수 있는데 여기서 변수가 a1, a0 두 가지이므로
각각의 변수에 대해 편미분한 것이 모두 0이 된다는 관계식을 통해 a1와 a0를 결정할 수 있습니다.
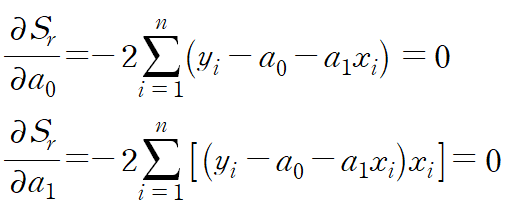
이것을 정리하면 아래와 같은 식을 얻습니다.
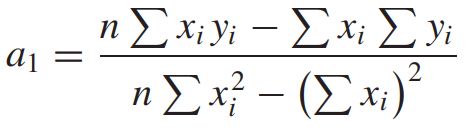

이것이 선형회귀입니다.
비선형회귀는 직선이 아닌 다른 곡선으로 x와 y의 관계를 가정하고 상수들을 찾는 것입니다.
1. Nonlinear Regression
비선형 회귀 곡선으로는 이차함수, 삼차함수, 삼각함수, 지수함수, 로그함수 등 여러가지 모델이 가능합니다.
직선이 아닌 모든 곡선이 비선형이기 때문에 모든 비선형 회귀모델을 정의하는 것은 의미가 없고 각각의 데이터 형태에 맞는 회귀모델을 사용하는 것이 중요합니다.
비선형 회귀의 과정은 다음과 같습니다.
1) 적절한 회귀모델을 고르고 선형회귀와 같은 형태로 변환한다.(로그, 역수 등 여러 방법으로)
2) 주어진 데이터를 같은 방법으로 변환하여 변환된 선형회귀식의 계수를 결정한다.
3) 변환된 선형회귀식의 계수로부터 기존 비선형 회귀모델의 계수를 결정한다.(역변환)
선형회귀와 마찬가지로 수행하게 되는데 차이점은 변환과정이 있다는 것입니다.
주의할 것은 데이터도 변환해주어야 한다는 것과 마지막 계수를 역변환으로 구한다는 것입니다.
여기서는 exponential model, power model에 더해 일반적인 nonlinear model까지 세 가지 예제를 소개하겠습니다.
> exponential model
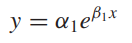
양변에 로그를 취하여 선형화합니다.
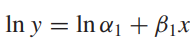
> power model
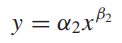
양변에 로그를 취하여 선형화합니다.
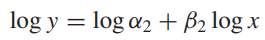
exponential에서는 자연로그를, power에서는 상용로그를 취하였는데 일반적으로 이렇게 회귀를 한다는 것이지 계수를 결정하는데 큰 의미는 없습니다.
2. Examples
(예제 1) 다음과 같은 데이터가 주어져있을 때 박테리아의 밀도 c와 시간 t의 관계를 나타내는 회귀곡선을 결정해라
이때 t와 c는 exponential model을 따른다고 가정한다.

exponential model은 다음과 같습니다. 우리의 목표는 α1과 β1을 구하는 것입니다.
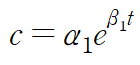
먼저 양변에 로그를 취하여 선형화합니다.
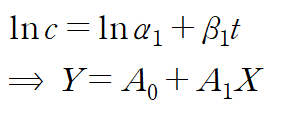
이 변환과정은 다음과 같이 정리할 수 있습니다.
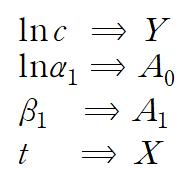
이 변환과정에 맞추어 데이터를 변환합니다.

이 변환된 데이터를 가지고 X,Y에 대한 선형회귀를 수행하여 A0, A1를 구한 후 α1과 β1을 구하면 됩니다.
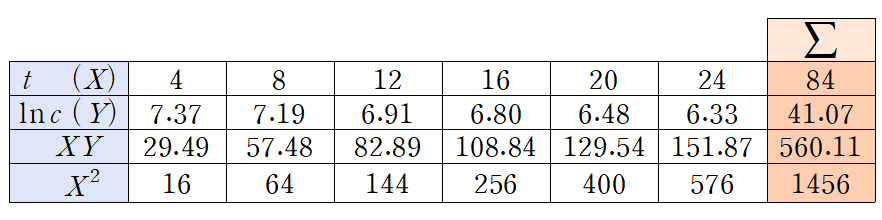
앞선 선형회귀 공식을 사용하기 위해서는
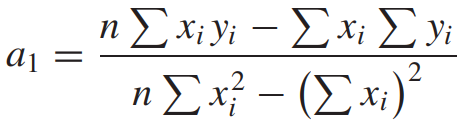
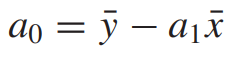
Σxy, Σx, Σy 등여러 부분합 정보가 필요하기 때문에 이것을 계산해줍니다.
아래 변환된 선형 회귀직선의 A0, A1를 구하는 겁니다.
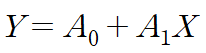
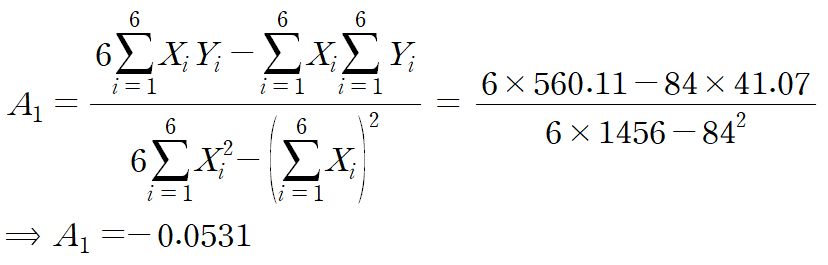
A0 공식의 짝대기 붙은 것들은 각각의 평균을 의미합니다(y bar, x bar라 읽습니다)
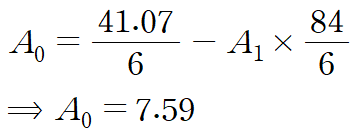
우리가 궁극적으로 구하고자 하는 것은 α1과 β1 이고, 이것은 처음 정의한 변환 관계식으로부터 얻을 수 있습니다.
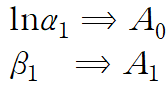
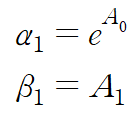
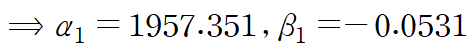
따라서 최종 회귀곡선은 다음과 같습니다.
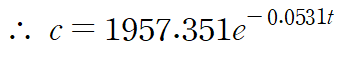
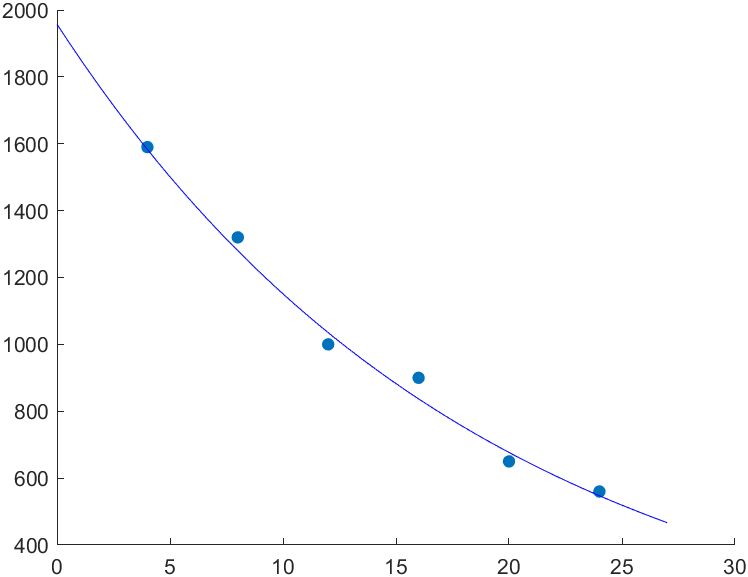
주어진 데이터와 회귀곡선을 표현하면 다음과 같습니다.
(예제 2) 다음과 같은 (x,y) 데이터가 주어졌을때 power model을 사용하여 회귀곡선을 결정하여라.
이때 선형화를 위해 상용로그를 사용하여라.
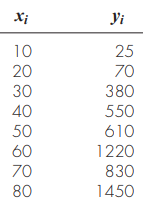
power model은 다음과 같습니다.
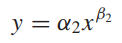
상용로그를 취해 선형화합니다.
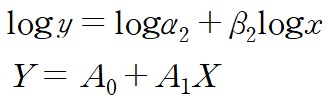
새로 정의된 변수간의 관계는 다음과 같습니다.
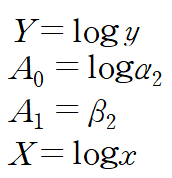
앞선 예제와 마찬가지로 데이터도 선형화해주는데 이 예제부터는 매트랩을 사용하겠습니다.
먼저 데이터를 정의하고(x,y) 상용로그를 취해 변환해줍니다.(X,Y)

여기서 log10 함수는 상용로그를 반환하는 함수입니다.
다음으로는 선형회귀를 수행해주는 fitlm 함수를 사용합니다.

이것저것 반환해주는데 추정된 계수의 Estimate 열에서 (Intercept)가 A0, x1가 A1에 해당합니다.
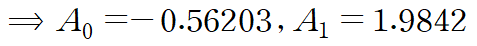
마지막으로 구하고자하는 계수들로 역변환해줍니다.
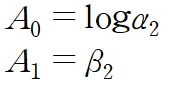
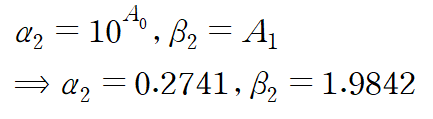
따라서 구하고자 하는 회귀곡선은 다음과 같습니다.

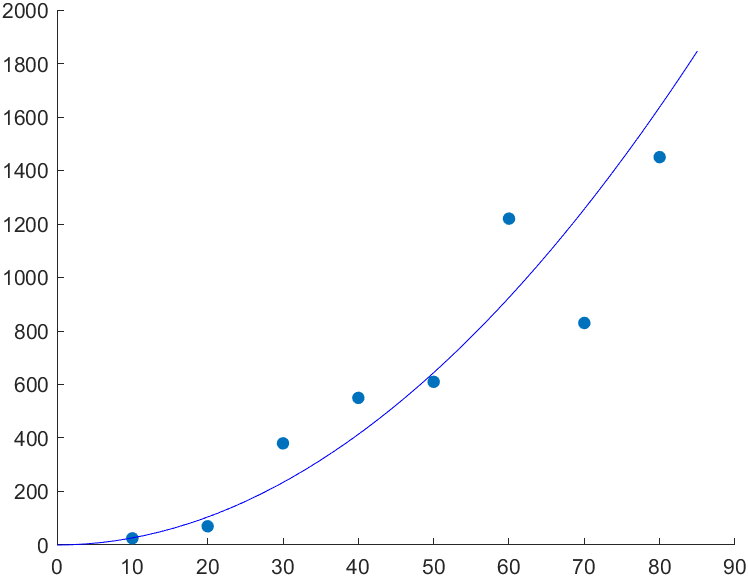
주어진 데이터와 대략적인 회귀곡선을 함께 나타내면 아래 그림과 같습니다.
(예제 3) 아래 표는 박테리아 성장율(k)와 산소 농도(c)에 관한 데이터이다.
이때 주어진 관계식을 이용하여 회귀곡선을 결정하여라.

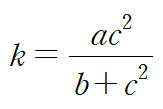
주어진 관계식의 양변에 역수를 취해봅시다.
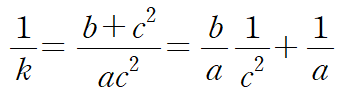

변수(c,k)가 분리되었고 이것을 직선 형태로 간주할 수 있으니 선형화된 것으로 봐도 무방하겠습니다.
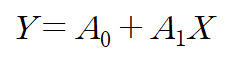
이때 각각의 변수의 변환 관계식은 다음과 같습니다.

마찬가지로 변수들의 데이터를 입력하고(c,k)

입력한 데이터를 변환합니다(X,Y)
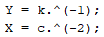
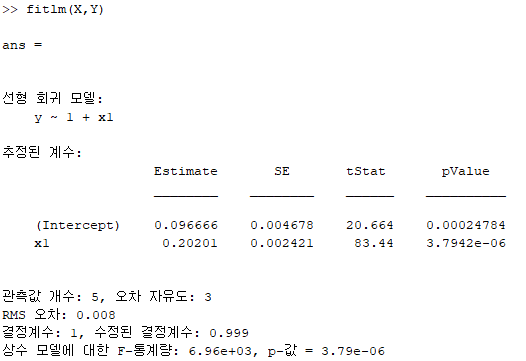
그 다음 fitlm 함수를 사용해 A0, A1를 얻습니다.
이렇게 얻은 A0, A1에 역변환 과정을 수행해 a,b를 얻습니다.
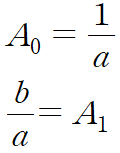
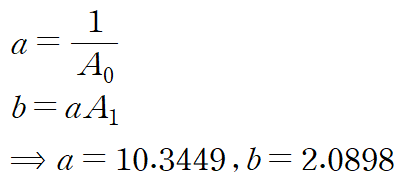
따라서 회귀곡선은 다음과 같습니다.

데이터와 회귀곡선을 함께 나타내면 아래 그림과 같습니다.

'MATHEMATICS > 수치해석학' 카테고리의 다른 글
| [수치해석] 가우스-자이델 방법, 야코비 반복법(Gauss-Seidel Method, Jacobi Iteration) (0) | 2023.08.06 |
|---|---|
| [수치해석] 다항회귀 예제(Polynomial Regression), 매트랩 코드 (0) | 2023.07.29 |
| [수치해석] 룽게-쿠타 방법(Runge-Kutta Method), 룽게 쿠타 4차 예제 (0) | 2023.06.08 |
| [수치해석학] LU분해(LU Factorization), 파이썬 코드 (1) | 2023.01.26 |
| [수치해석학] 뉴턴-코츠 공식, 심슨 룰(Newton-Cotes Formula, Simpson's Rule) (1) | 2021.12.25 |