0. Introduction
데이터의 분포에 따라 회귀모델을 직선이 아니라 다항함수로 설정하는 것이 더 유용할 때가 있습니다.

지난 게시글에서는 exponential, power 등 일반적인 비선형 회귀 모델에 대해 선형화를 진행하고 계수를 구하는 예제를 소개했었는데
오늘은 비선형 회귀 모델 중 다항함수 모델에 대해 소개하겠습니다.
1. Polynomial Regression
> 회귀곡선을 이차함수라 가정

회귀곡선을 이차함수라 가정한 경우 a0, a1, a2 총 세 개의 계수를 결정해야 합니다.
아래 제곱합을 가지고 계수를 결정합니다.

세 개의 변수 a0, a1, a2에 대해 편미분을 수행하고, 이것이 각각 0이라는 방정식을 세우고 연립하여 각각의 계수들을 구할 수 있습니다.
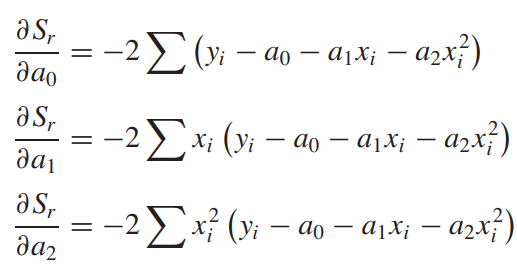
이를 정리하면 아래와 같은 연립방정식이 유도되며 이는 행렬 연산을 통해 간단히 풀 수 있습니다.
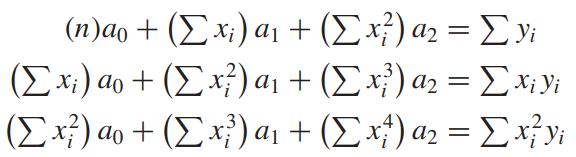
> 회귀곡선을 m차함수라 가정
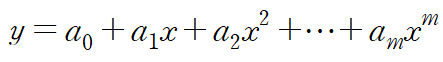
회귀곡선을 m차함수라 가정한경우 a0, a1, . . . , am 총 (m+1) 개의 계수를 결정해야 합니다.
2. Example
(예제) 주어진 데이터를 사용해 이차 회귀 곡선을 결정하여라

앞서 살펴본 연립방정식을 풀기 위해서 필요한 부분합들을 계산해주겠습니다.
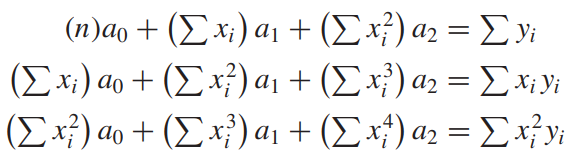

매트랩을 사용해 필요한 상수들을 미리 구해두겠습니다.
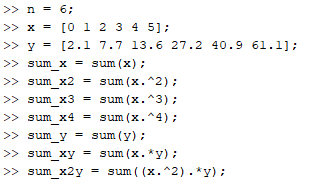
행렬을 수립하고

선형방정식의 해를 구합니다. 이 해가 곧 우리가 구하고자 하는 계수(a0, a1, a2)입니다.
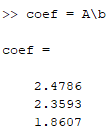
따라서 구하고자 하는 이차 회귀 곡선은 다음과 같습니다.
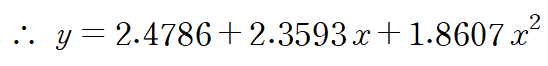
주어진 데이터와 회귀 곡선은 아래 그림과 같습니다.
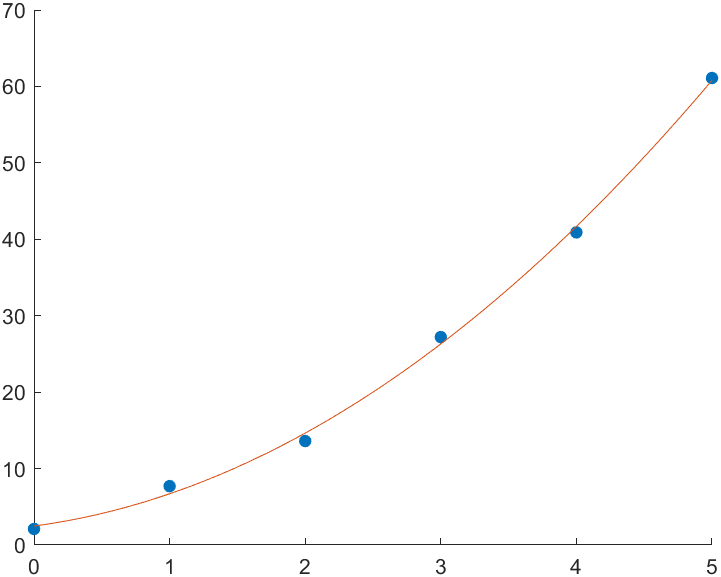
아래 명령어로 데이터 포인트와 회귀곡선을 함께 그릴 수 있습니다.
'MATHEMATICS > 수치해석학' 카테고리의 다른 글
| [수치해석] 가우스-자이델 방법, 야코비 반복법(Gauss-Seidel Method, Jacobi Iteration) (0) | 2023.08.06 |
|---|---|
| [수치해석] 비선형 회귀(Nonlinear Regression) 예제, 매트랩 코드 (0) | 2023.07.27 |
| [수치해석] 룽게-쿠타 방법(Runge-Kutta Method), 룽게 쿠타 4차 예제 (0) | 2023.06.08 |
| [수치해석학] LU분해(LU Factorization), 파이썬 코드 (1) | 2023.01.26 |
| [수치해석학] 뉴턴-코츠 공식, 심슨 룰(Newton-Cotes Formula, Simpson's Rule) (1) | 2021.12.25 |