#미분적분학
#미적분학
1. Disk Method
회전축에 수직으로 자른 단면을 쌓는 방식이기 때문에 disk method라고 부릅니다.
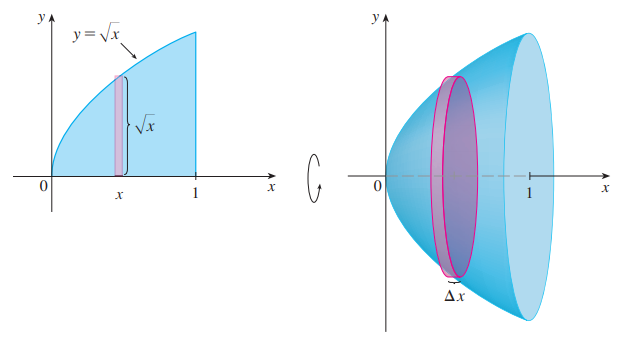
먼저 기본 공식을 살펴봅시다.
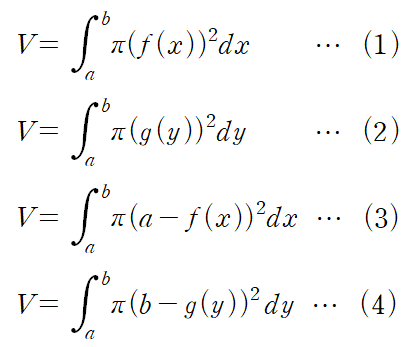
(1) : y = f(x)를 x축에 대해 회전시킨 경우
(2) : x = g(y)를 y축에 대해 회전시킨 경우
(3) : y = f(x)를 y = a 에 대해 회전시킨 경우
(4) : x = g(y)를 x축에 대해 회전시킨 경우
※ 축이 영역을 가로지르는 경우는 생각하지 않습니다.
두 곡선으로 둘러싸인 영역을 회전시킬 경우 다음과 같습니다.
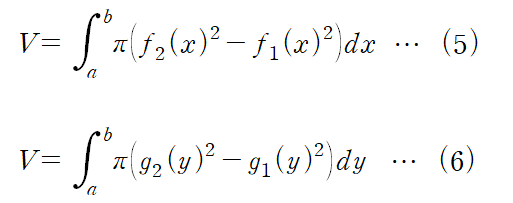
(5) : y = f2(x)와 y = f1(x) 사이의 영역을 회전시킨 경우. f2가 f1보다 회전축에서 멀리 있어야 합니다(outer radius > inner radius)
(6) : x = g2(y)와 x = g1(y) 사이의 영역을 회전시킨 경우. g2가 g1보다 회전축에서 멀리 있어야 합니다(outer radius > inner radius)
※ 두 곡선이 구간 [a,b]에서 교차하는 경우는 생각하지 않습니다.
각 경우에 대한 예제를 풀어보겠습니다.
(예제 1) 아래 곡선들로 둘러싸인 영역을 x축에 대해 한 바퀴 회전시킨 회전체의 부피를 구하여라
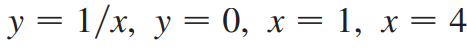
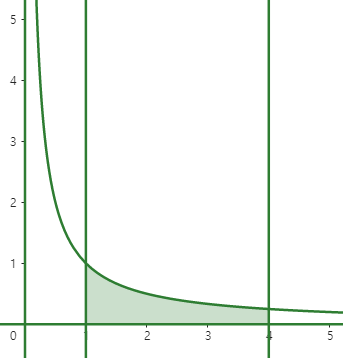
위 영역을 x축에 대해 회전시킨 회전체의 부피는 다음과 같습니다.
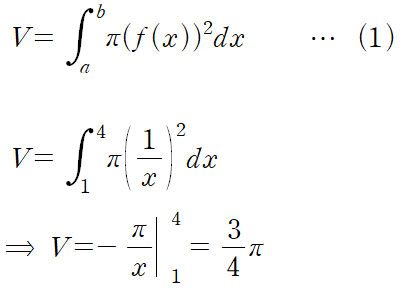
(예제 2) 아래 곡선들로 둘러싸인 영역을 y축에 대해 한 바퀴 회전시킨 회전체의 부피를 구하여라
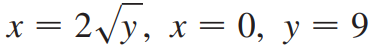
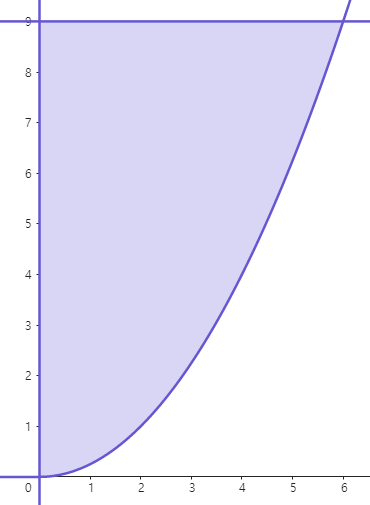
위 영역을 y축에 대해 회전시킨 회전체의 부피는 다음과 같습니다.
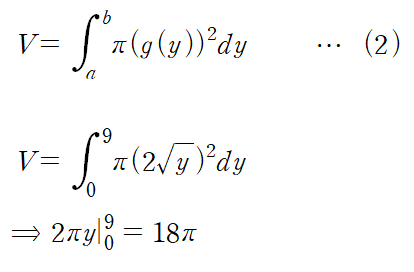
(예제 3) 아래 곡선들로 둘러싸인 영역을 y = -3 에 대해 한 바퀴 회전시킨 회전체의 부피를 구하여라
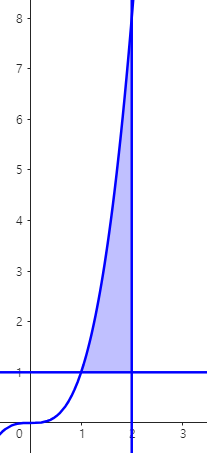
위 영역을 y = -3에 대해 회전시킨 회전체의 부피는 다음과 같습니다.
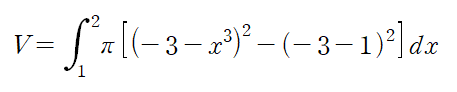
영역을 y = -3에 대해 회전시키게 되면 도넛처럼 빈 공간이 나오게 됩니다. 이 빈공간을 빼줘야 하기 때문에 다음과 같은 식을 사용하여 회전체의 부피를 계산할 수 있습니다.
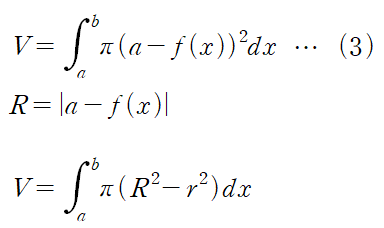
이때 R은 바깥쪽 반지름, r은 안쪽 반지름입니다.
이 문제의 경우 다음과 같이 반지름을 구할 수 있습니다.
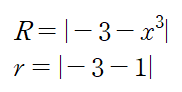
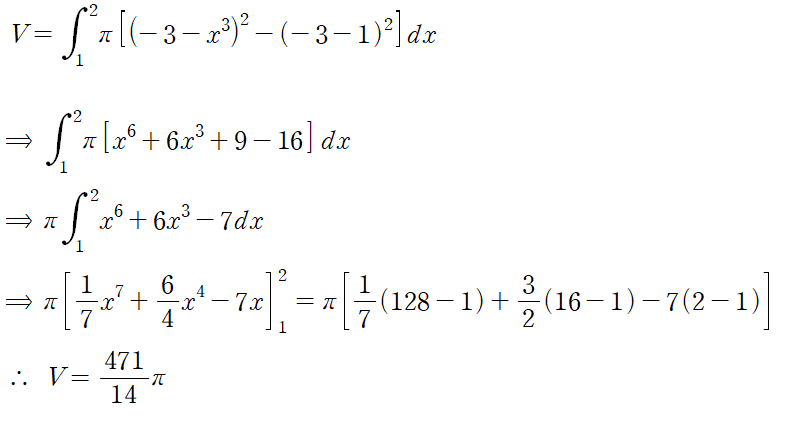
(예제 4) 아래 곡선들로 둘러싸인 영역을 x = 2 에 대해 한 바퀴 회전시킨 회전체의 부피를 구하여라
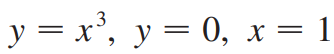
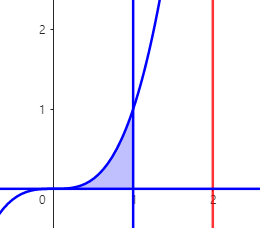
위 영역을 x = 2에 대해 회전시킨 회전체의 부피는 다음과 같습니다.
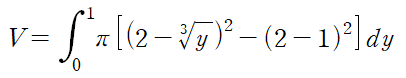
예제 3과 마찬가지로 중심부의 빈 공간을 빼주어야 합니다.
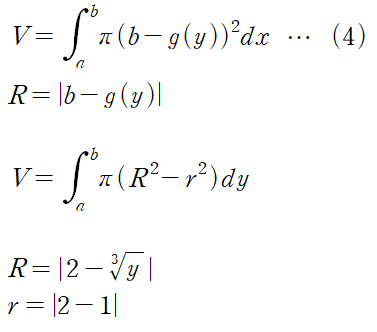
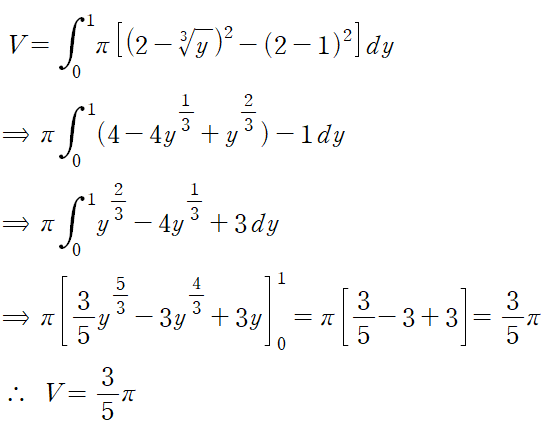
(예제 5) 아래 곡선들로 둘러싸인 영역을 x축에 대해 한 바퀴 회전시킨 회전체의 부피를 구하여라
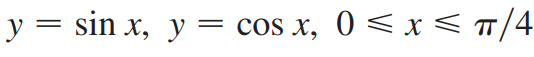
위 영역을 x축에 대해 회전시킨 회전체의 부피는 다음과 같습니다.
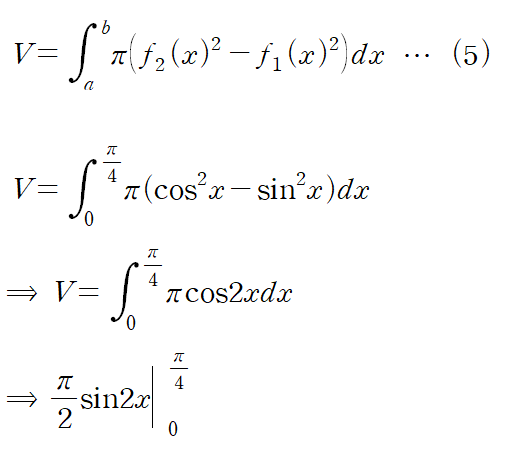
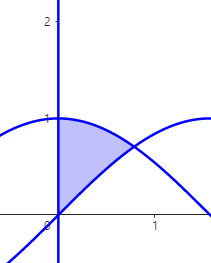
(예제 6) 아래 곡선들로 둘러싸인 영역을 y축에 대해 한 바퀴 회전시킨 회전체의 부피를 구하여라
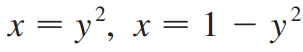
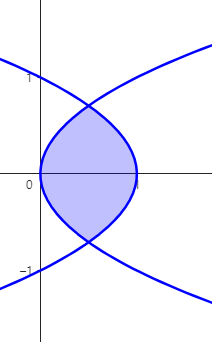
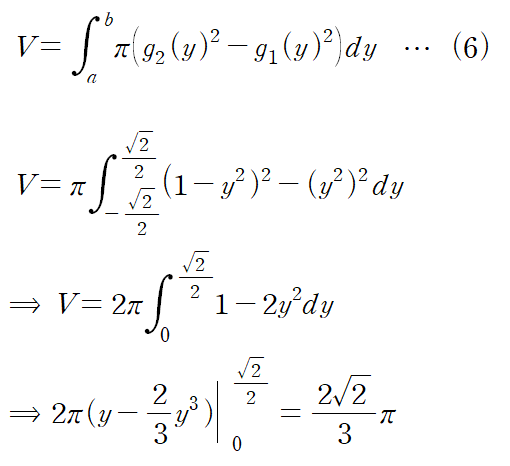
2. Cylindrical Shell Method
원통셸 방법, 원통껍질 방법으로 번역되는 cylindrical shell method(또는 간단히 shell method)는 앞서 소개한 disk method로 부피를 계산하기 어려운 회전체에 적용할 수 있습니다.
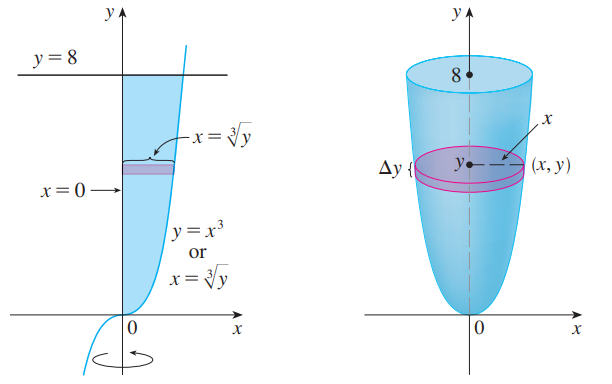
예를 들면 아래 그림이 나타내는 영역을 y축으로 회전시켜 얻은 회전체의 부피를 구하는 것은 기존 disk method로 풀려면 x = g(y) 꼴의 함수를 얻어야만 하는데 이는 삼차방정식의 해로부터 얻어지며 또한 회전체 내부, 외부의 x 좌표를 각각 이끌어내는 것이 쉽지 않습니다.
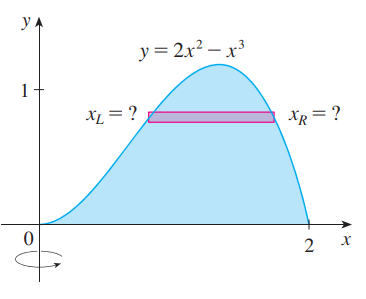
이러한 경우에 회전체를 회전축을 중심으로 속이 빈 얇은 원통으로 쪼개는 cylindrical shell method 를 이용해 부피를 구할 수 있습니다.
아래와 같이 y = f(x), x = a, x = b, y = 0으로 둘러싸인 영역을 y축에 대해 회전한 회전체의 부피를 구해봅시다.
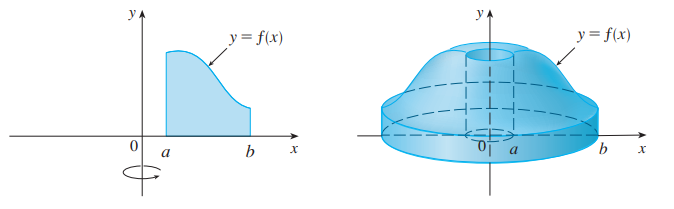
아래 그림과 같이 회전체를 분할할 수가 있습니다.
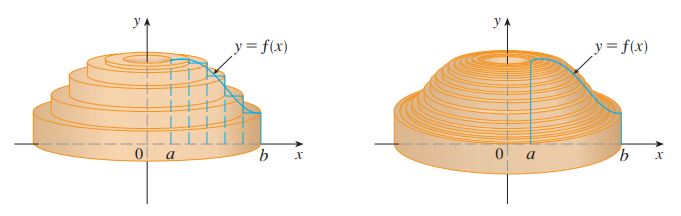
회전체의 부피 V는 속이 빈 얇은 원통의 부피의 합으로 표현할 수 있습니다.
이 두께가 얇은 원통의 부피는 (밑면의 둘레 * 높이 * 두께(이 경우 dx))로 근사됩니다.
밑면의 둘레는 2πr, 높이는 h입니다.
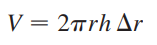
위 그림의 경우 다음과 같이 dx로 부피를 표현할 수 있습니다.
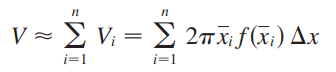
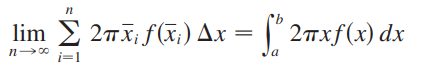
원통셸 방법에서는 아래 식만 기억하면 됩니다.
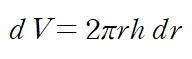
r은 회전축에서 임의의 점까지의 수직 거리
h는 임의의 점에서 원통의 높이
dr은 r의 방향에 따라 dx 또는 dy로 정해집니다.
(예제 7) 아래 그림과 같이 둘러싸인 영역을 y축에 대해 회전한 회전체의 부피를 구하여라
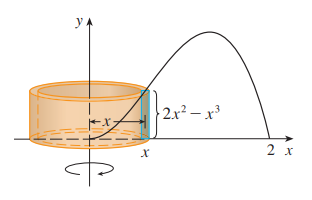
조건을 정리하고
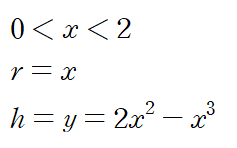
dV = 2πrh dr에 적용합니다.

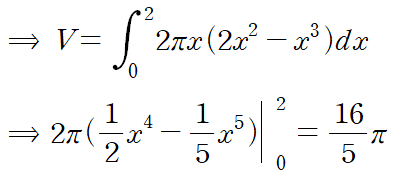
(예제 8) 두 곡선으로 둘러싸인 영역을 y = -2 에 대해 회전한 회전체의 부피를 구하여라
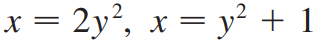
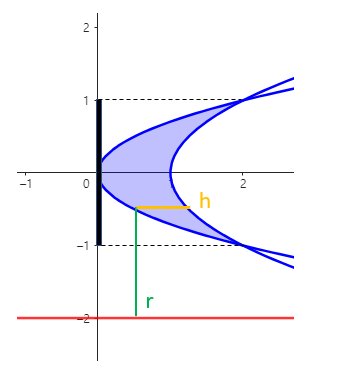
y의 범위는 [-1, 1]이고 r은 y-(-2) = y+2 , h는 y^2+1 - 2y^2입니다.
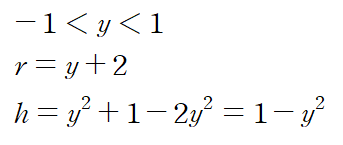
미소부피를 설정하고 적분합니다.
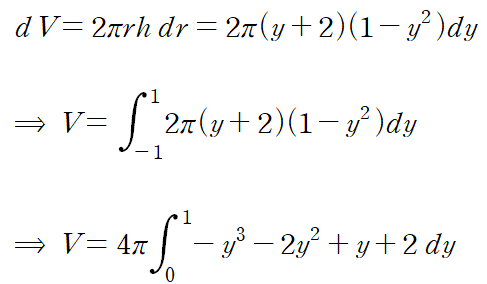
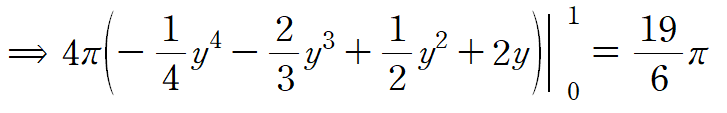
오타, 계산오류 등 지적 감사히 받습니다
'MATHEMATICS > 미분적분학' 카테고리의 다른 글
| 미분적분학 멱급수와 수렴반경 쉽게 이해하기 - Power Series, Radius of Convergence (1) | 2024.10.21 |
|---|---|
| [미분적분학] 삼각함수 어려운 적분(Trigonometric Integrals), 삼각 적분 (0) | 2023.08.03 |
| [미분적분학] 방향도함수 (Directional Derivative) (0) | 2022.07.28 |
| [미분적분학] 그린정리(Green's Theorem) 예제 (0) | 2021.12.23 |
| [미분적분학] 라그랑주 승수법 예제 (0) | 2021.12.12 |