오늘 다룰 내용은 보간법의 일종인 라그랑주 다항식 입니다. 보간법(Interpolating)은 간단히 몇 개의 점이 주어졌을 때 그것을 관통하는 함수를 세워 discrete한 데이터들을 연속적인 데이터로 근사하거나 미래의 데이터를 추측하는 것을 말합니다.
예를 들어 아래와 같이 세 데이터가 주어졌을 때

보간법의 일종인 라그랑주 다항식을 세우면 다음과 같이 세 데이터를 지나는 함수를 세울 수 있습니다.

1. 라그랑주 다항식의 정의
라그랑주 다항식은 다음과 같이 정의됩니다

이때 Ln,k 는 아래와 같습니다. 이를 가중함수(weight function)이라고도 부르고 라그랑주 기저다항식이라 부르기도 합니다. 제가 배운 용어는 Lagrange Interpolating Polynomial 입니다.

위와 같은 식이 나오는 이유는 세워진 라그랑주 다항식에 xk를 넣은 값이 f(xk)여야 한다는 것으로 충분합니다. f(xk)는 xk 에서의 데이터를 말합니다.
Ln,k 는 아래와 같습니다.

Ln,k 에 xk 를 대입하면

이번에는 Ln,k 에 xm 을 대입해봅시다. (m≠k)

분자에 (x-xm)항이 존재하기 때문에 Ln,k 에 xm 를 대입하면 0이 됩니다. 이는 거꾸로 생각해보면 모든 k에 대해 (0≤k≤n) 세워지는 Ln,k 는 xk 가아닌 데이터를 대입하면 모두 0이 된다는 것을 의미합니다.

Ln,k 의 계수가 f(xk) 이므로
이상의 결과를 종합하면 다음과 같습니다.

2. 예제 풀이
도입부에 사용한 데이터를 가지고 라그랑주 다항식을 세워봅시다.
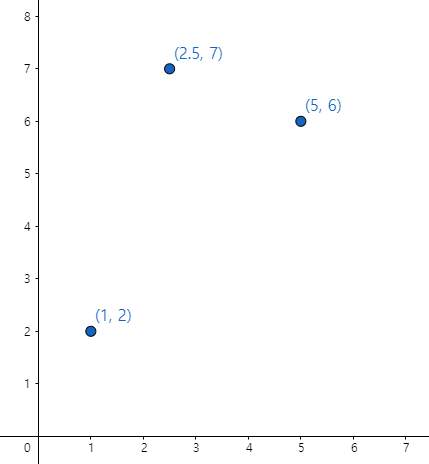
(1,2), (2.5,7), (5,6) 을 가지고 Ln,k 를 세우면

계산하여 정리하면
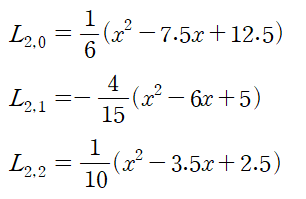
주어진 데이터와 L2,k 를 사용해 라그랑주 다항식을 세웁니다.

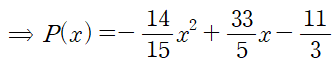
부록>> 파이썬 코드
얕은 지식으로나마 끙끙대며 코드를 작성해보았습니다.. 자그마치 78줄이나 되는 어마어마한 코드
import numpy as np
def num(x_data): # 분자
xd = x_data
n = len(xd)
num_0 = []
for k in range(0, n):
p = []
k_list = list(range(0, n))
k_list.remove(k)
for i in k_list:
p.extend(np.poly1d(xd[i]))
num_0.append(np.poly(p))
num_0 = np.array(num_0)
return (num_0)
def den(x_data): # 분모
xd = x_data
n = len(xd)
den = []
for k in range(0, n):
den_list = []
k_list = list(range(0, n))
k_list.remove(k)
for i in k_list:
den_list.append(1 / (xd[k] - xd[i]))
den.append(np.prod(den_list))
den = np.array(den)
return (den)
def lp(): # 메인
x_data_str = []
print("Input x data")
print("If you input the all data, type 'end' ")
while 1:
x_data_str.append(input(": "))
if "end" in x_data_str:
break
if "" in x_data_str:
x_data_str.remove("")
x_data_str.remove("end")
n = len(x_data_str)
x_data = [float(item) for item in x_data_str]
y_data_str = []
print("Input y data corresponding to x data")
for i in range(0, n):
y_data_str.append(input(": "))
if "end" in y_data_str:
break
if "" in y_data_str:
y_data_str.remove("")
y_data = [float(item) for item in y_data_str]
y_data = np.array(y_data)
de = den(x_data)
nu = num(x_data)
L = (nu.T * de).T
P1 = (L.T * y_data).T
P = P1.sum(axis = 0)
P2 = np.poly1d(P)
print(P2)
return P2 #Lagrange Polynomial
lp()
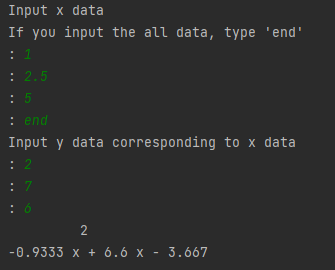
리스트 안의 리스트 형태를 잘 활용하지 못해서 그냥 x 값을 한 번에 인풋하는 형식으로 작성했습니다.
아래 사진은 앞서 다룬 예제의 데이터를 넣어 얻은 라그랑주 다항식.
'MATHEMATICS > 수치해석학' 카테고리의 다른 글
| [수치해석] 비선형 회귀(Nonlinear Regression) 예제, 매트랩 코드 (0) | 2023.07.27 |
|---|---|
| [수치해석] 룽게-쿠타 방법(Runge-Kutta Method), 룽게 쿠타 4차 예제 (0) | 2023.06.08 |
| [수치해석학] LU분해(LU Factorization), 파이썬 코드 (1) | 2023.01.26 |
| [수치해석학] 뉴턴-코츠 공식, 심슨 룰(Newton-Cotes Formula, Simpson's Rule) (1) | 2021.12.25 |
| [수치해석학] 뉴턴 보간법 (Newton's Interpolating Polynomial, Divided difference) (0) | 2021.12.16 |