이번 글에서는 멱급수와 멱급수의 수렴반경을 알아봅시다.
목차
1. 서론
2. 멱급수를 간단한 함수로 표현하기
3. 멱급수의 수렴
1. 서론
멱급수(power series)는 다음과 같이 다항함수들의 합으로 표현된 급수를 말합니다.

Cn은 x^n의 계수입니다.
멱급수는 x의 값에 따라 수렴할수도 있고, 발산할 수도 있습니다.
급수의 수렴/발산을 조사하는 여러 가지 test가 있습니다.
[미분적분학] 교대급수 판정법
#미분적분학 오늘은 무한급수의 합이 수렴하는지, 발산하는지 알 수 있는 판정법(Test) 중 교대급수 판정...
blog.naver.com
이러한 test들을 사용하여 멱급수의 수렴/발산을 조사할 수 있습니다.
예를 들어 Cn =1인 경우, 이것을 첫째항이 1, 공비가 x인 등비급수로 본다면 -1<x<1에서 x가 수렴합니다.

아래와 같은 멱급수의 경우 ratio test로 수렴하는 x의 구간을 구할 수 있습니다.



오직 x = 0인 경우에서만 수렴하는 것을 확인할 수 있습니다.
2. 멱급수를 간단한 함수로 표현하기
여러가지 방법이 있지만, 간단히 기하급수 방법을 사용하여 하나의 간단한 함수로 표현할 수 있습니다.
> 기하급수의 계산과 수렴하는 r의 범위

a는 첫째항, r은 공비입니다.
(예제 1) 기하급수가 수렴한다면, 그 값을 계산하여라

공비가 1/3이므로 주어진 기하급수는 수렴하고, 그 값은 다음과 같습니다.
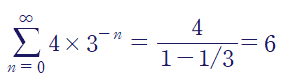
위 예제가 이해되었다면, 서론에서 설명한 케이스도 이해가 될겁니다.
x를 공비로 두면 급수의 첫째항이 1이 되는 거죠
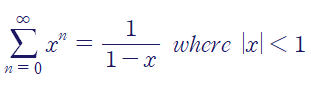
(예제 2) 멱급수를 간단한 함수로 표현하여라라
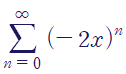
앞선 예시와 마찬가지로 첫째항이 1, 공비가 -2x이기 때문에 아래와 같이 간단한 함수로 표현할 수 있습니다.
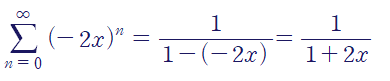
이 멱급수가 수렴하는 구간은 -1/2<x<1/2입니다.
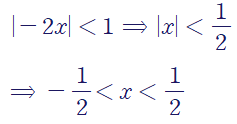
(예제 3) 멱급수를 간단한 함수로 표현하여라
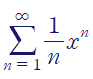
멱급수를 미분하여 간단한 함수로 표현할 수 있습니다.
주어진 멱급수를 f(x)라 합시다.
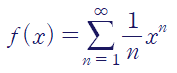
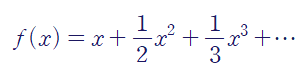
양변을 미분하면 우리가 잘 알고 있는 간단한 형태의 멱급수를 얻습니다.
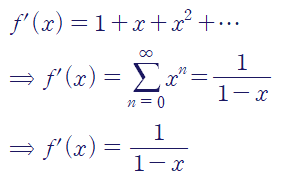
양변을 적분하고
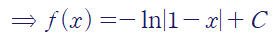
적분상수를 처리해서 주어진 멱급수를 간단한 함수로 표현할 수 있습니다.
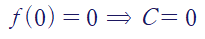
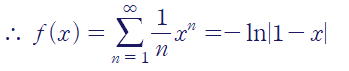
3. 멱급수의 수렴
멱급수의 수렴은 세 가지 케이스가 있습니다.
I) 한 점에서 수렴 x=a
II) 수렴반경 |x-a|<R에서 수렴
III) 모든 실수에서 수렴 (-∞,∞)
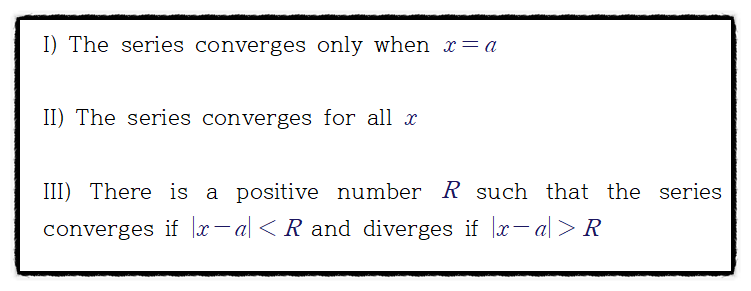
마지막 케이스 III)에서, 수렴구간 양 끝에서의 수렴은 별도로 확인해야만 알 수 있습니다.
양쪽 끝에서 모두 수렴, 양쪽 끝에서 모두 발산, 한쪽 끝에서만 수렴하는 경우로 나눠집니다.

정리하면, x=a에서는 항상 수렴하고 그 외의 범위는 별도의 test를 통해 알아내야 합니다.
첫 번째 케이스 I)에서 수렴반경 R = 0이고 두 번째 케이스 II)에서 수렴반경 R = ∞입니다.
(예제 4) 급수의 수렴반경과 수렴하는 구간을 구하여라
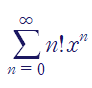
Ratio test를 이용하여 수렴반경을 구할 수 있습니다.
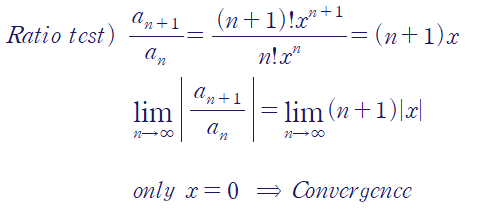
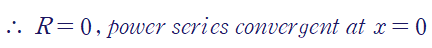
(예제 5) 급수의 수렴반경과 수렴하는 구간을 구하여라
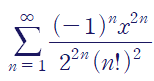
마찬가지로 비판정법(ratio test)을 사용합시다
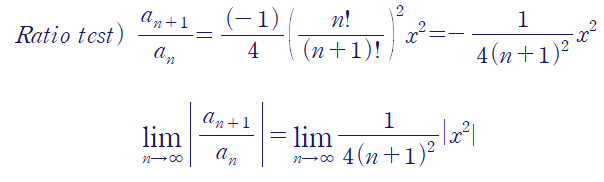
이로써 주어진 멱급수가 모든 x에 대해 수렴한다는 것을 확인할 수 있습니다.
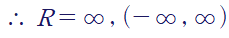
(예제 6) 급수의 수렴반경과 수렴하는 구간을 구하여라
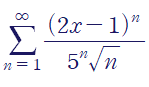
마찬가지로 비판정법(ratio test)를 사용합니다.
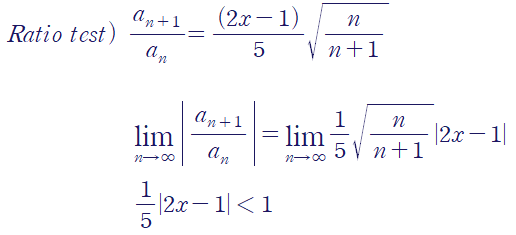
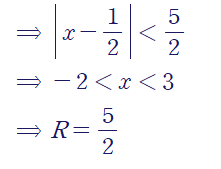
여기서 R을 5이라고 하지 않도록 주의해야 합니다.
부등식에서 x의 계수를 1로 만들었을 때의 우변이 R이라는 것을 기억하세요
이제 양끝에서의 수렴/발산을 조사합시다.
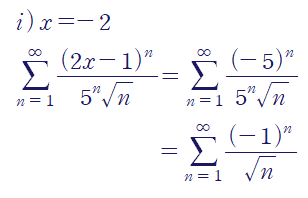
x =-2일 때, "교대급수 판정법"에 의해 급수는 수렴합니다.
간단히 설명하자면, 급수의 수열이 (1)감소하고, (2)부호가 계속해서 바뀌면 그 급수는 수렴합니다.
자세한 내용은 아래 글 참조 바랍니다.
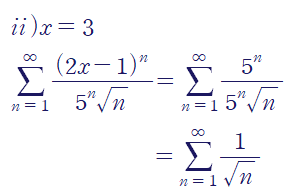
p-test에 의해 (p=1/2 < 1) 해당 급수는 발산합니다.
따라서 x =-2에서 수렴, x =3에서 발산합니다.
최종적인 수렴반경과 급수의 수렴구간은 다음과 같습니다.
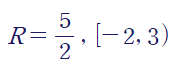
'MATHEMATICS > 미분적분학' 카테고리의 다른 글
| [미분적분학] 삼각함수 어려운 적분(Trigonometric Integrals), 삼각 적분 (0) | 2023.08.03 |
|---|---|
| [미분적분학] 회전체 부피 구하기 : 디스크, 원통셸 방법 (4) | 2023.01.10 |
| [미분적분학] 방향도함수 (Directional Derivative) (0) | 2022.07.28 |
| [미분적분학] 그린정리(Green's Theorem) 예제 (0) | 2021.12.23 |
| [미분적분학] 라그랑주 승수법 예제 (0) | 2021.12.12 |