반응형
#편입수학
※ 중앙대 2023학년도 편입 기출입니다

거리 문제의 포인트는 다음 세 가지 입니다.
(1) 목적함수를 "거리의 제곱"으로 두기
(2) 케이스 누락되지 않도록
(3) 보기를 통해 눈치로 케이스 좁히기
라그랑주 승수법을 통해 최대, 최소를 구하는 방법은 다음과 같습니다.
(1) 목적함수 f(x,y) 와 제약조건 g(x,y) 정리
(2) 함수 L 설정
(3) x,y,λ 에 대해 각각 편미분한 것 = 0
(4) 최대, 최소 고르기
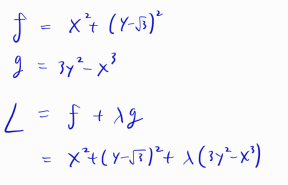
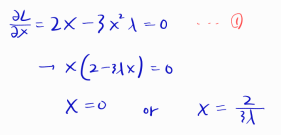
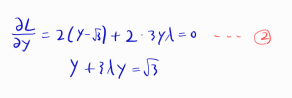

L을 x로 편미분한 식에서 두 가지 케이스가 나옵니다.
x = 0이거나 x = 2/3λ 이거나.
먼저 x = 0에 대해 최소를 구하면 루트 3이 나오는데,
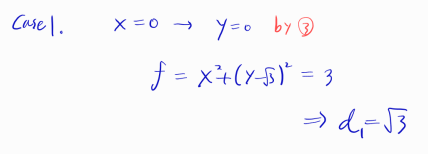
보기에 루트 3이 없으니 두 번째 케이스라는 것을 눈치로 알 수 있습니다.

또다시 y가 양수, 음수인 두 가지 케이스로 분기가 되는데
이때 목적함수를 생각해보면 y가 양수인 케이스가 최소 거리가 될 것임을 예상할 수 있습니다.
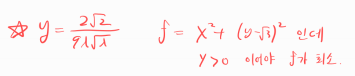
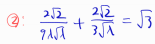
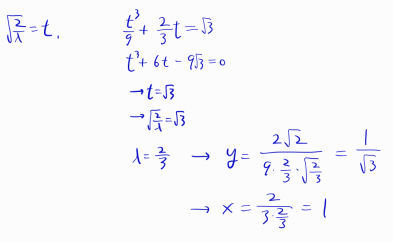
따라서 최소 거리는 다음과 같습니다.
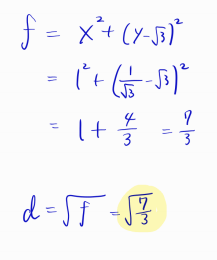
반응형
'MATHEMATICS > 편입수학' 카테고리의 다른 글
| [편입수학] 한양대 2023학년도 완전미분방정식 (1) | 2024.03.26 |
|---|---|
| [편입수학] 한양대 2023학년도 행렬식 구하기 (0) | 2024.03.25 |
| [건국대 편입 기출] 매개변수 곡선의 접선 (0) | 2023.12.27 |