지난 시간에 이어 수학 가형에서 제시해주는 '미분가능'조건을 어떻게 해석해야 좋은가를 알아보자. 솔직히 나형처럼 구간을 나눠서 미분가능->연속조건을 사용하는 호락호락한 문제는 그렇게 많지 않다. 오히려 미분가능하다는 것이 무엇인지 그 정의에 대해 알고있어야 하는 경우가 많다. 가형에서 미분가능 조건이 제시되는 경우는 최근 기출을 봤을 때 합성함수의 미분, 역함수의 미분이 자주 출제되고, 가끔 고난도문제에서 절댓값기호가 포함된 함수의 미분 정도? 일단 기출을 통해 어떤 방식으로 출제되는지 알아보자

2021학년도 6월 수학가형 11번

2020학년도 수능 수학가형 17번

2020학년도 수능 수학가형 21번

2020학년도 수능 수학가형 26번

2020학년도 9월 수학가형 17번

2020학년도 9월 수학가형 30번

2020학년도 6월 수학가형 9번

2020학년도 6월 수학가형 16번

2020학년도 6월 수학가형 20번
수학 나형과 비교해봤을 때 미분가능이라는 조건이 훨씬 많이 등장한다. 핵심적인 개념으로 나오지는 않더라도, 문제를 "정확히"풀기 위해서 미분가능 조건을 제시해주는 경우도 있다. 주어진 함수가 미분가능한지 어떤지 파악하지도 않고 무조건 미분하는 학생들이 있는데, 그런 식으로 제대로 공부하지 않은 학생들을 위한 건 아니다. "이 함수는 미분할 수 있으니 필요하다면 미분해보세요"라는 뉘앙스로 제시해주는 경우가 많은 것이다. 제대로 공부한 학생이라면 마구잡이로 보자마자 미분하지는 않는다. 가장 최근에 출제된 2021학년도 6월 수학가형 11번 또한 그런 느낌으로 미분가능 조건을 제시한다

2021학년도 6월 수학가형 11번
답을 구하는 과정에 있어서 f(x)가 미분가능한지, g(x)가 미분가능한지 따질 필요는 사실 없다. 그냥 마구잡이로 양변을 미분해서 x=0을 대입하면 답이 나오니까. 하지만 그런 식으로 공부해서는 발전할 수 없다. 논리적으로 사고해서 미분가능하므로 미분을 하는 학생이 발전할 수 있다. 그런 학생들은 수리논술에서도 좋은 점수를 받아간다. 대학교에 입학하고 나서 기초수학과목을 들을 때도 좋은 점수를 받아간다. 미분가능이란 조건은 그런 거다.
먼저 미분가능하기 위한 조건의 정의를 보자

미분이라는 것은 극한값을 계산하는 것이다. 즉 x=a에서 미분계수는 x=a에서의 어떤 극한값이 된다. 이 극한값이 존재한다는 것은 좌극한과 우극한이 같다는 것을 의미하므로 위와 같은 조건이 성립하는 것이다. 근데 추가로 어떤 두 함수가 각각 미분가능할 때, 그 함수들의 곱 또한 미분가능하다는 사실을 알고 있는 학생은 그리 많지 않다.

2021학년도 6월 수학가형 11번
예를 들어보자. 위 문제의 g(x)는 f(x)를

로 나눈 것으로 정의된다.
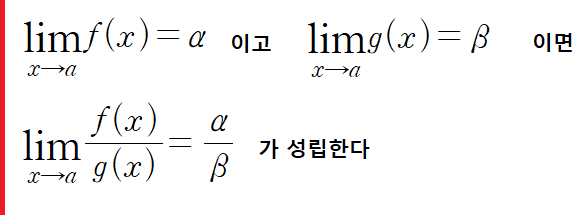
극한의 기본성질
그런데 극한의 기본성질에 의해서 두 함수로 만든 분수꼴의 극한값 또한 존재하게 된다. 따라서 미분가능한 두 함수의 곱 혹은 분수꼴은 다시 미분가능한 함수가 된다. 그래서 g(x)가 미분가능한 것이고, 그래서 g(x)를 미분해서 답을 구할 수 있는 것이다.

2020학년도 6월 수학가형 16번
이 문제도 마찬가지다. f(x), cos x, e^x 모두 실수전체의 집합에서 미분가능한 함수이므로 g(x)를 미분해도 되는것이다

2020학년도 9월 수학가형 17번
위 문제는 미분가능이라는 조건을 조금 특이하게 제시한다. 도함수가 연속이라는 말로 제시해주는데, 그 이유는 아마도 도함수를 적분하는 형태의 조건 (나) 때문일 것이다. 고등교육과정에서는 연속함수일 때만 적분이 가능하다고 배운다. 본 문제에서는 도함수 g'(x)를 적분하기 위해서 g'(x)가 연속이라는 조건이 필요하기 때문에 논리적 결함을(혹은 이의신청을) 없애고자 제시한 조건으로 보인다. 그렇다. 요즘엔 사실 나형에서처럼 그렇게 Critical한 조건으로 제시되는 건 아니다. 과거에는 절댓값함수의 미분가능성이 고난도 킬러문제에서 핫한 트렌드였는데, 4년 전 2017학년도 기출을 마지막으로 자취를 감춰버렸다. 간간히 사설모의고사에서 나오기도 하고 논술에서도 출제되는 유형이긴 한데 평가원에서는 이미 단물을 빨 만큼 빨았는지 해당 유형의 문제는 더 보이지 않는다.

2017학년도 9월 수학가형 30번
본 포스팅은 한국교육과정평가원이 주관하는 수능과 모의고사에 대해서 정보를 주는 포스팅이기 때문에 절댓값함수의 미분가능성 까지 설명하지는 않는다. 나중에 논술 문제에서 다루게 되면 그때 더 자세하게 절댓값함수에 대해서 다뤄볼 예정이다.
'MATHEMATICS > 고등수학' 카테고리의 다른 글
| [2023학년도 수능] 수학 미적분 29번 손글씨 풀이 (0) | 2022.12.19 |
|---|---|
| 2023학년도 고3 6월 모의고사 기하 29번 손글씨 풀이 (0) | 2022.08.31 |
| 수능에서 '미분가능' 조건의 해석 : 수학 나형 편 (0) | 2022.06.15 |