수학 가형과 나형에서 공통적으로 「실수 전체에서 미분가능한 함수 f(x)」 라던지, 「f(x)가 실수 전체에서 미분가능할 때」 같은 문장이 종종 등장한다. 공부를 제대로 하지 않은 학생은 이 문장을 그냥 "이 말은 맨날 나오네 문제 분량 채울 게 없나봐?" 혹은 "당연한 거 아냐? 어쩌라고!" 라고 생각하고 넘어가거나 생각조차 하지 않고 그냥 넘어가버린다. 하지만 이 문장은 정말 정말 정말 정말 중요한 문장이다.
문제를 푸는 어떤 "길"이 있다고 하자. 답으로 이르는 이 "길"은 중간중간에 답까지 잘 찾아갈 수 있도록 하는 중간중간에 "조건"이라는 장치가 있다. 일종의 표지판의 역할을 하는 "조건"을 찾지 못한다면 답까지 도달할 수 없다. "조건"들은 문제 곳곳에 처음부터 끝까지 보물찾기 마냥 숨어있다. 필자는 어릴 때 보물찾기를 해서 상품을 타본 적이 없는데 아무리 눈을 씻고 찾아봐도, 길길이 뛰고 날고 해도 도무지 상품이 적힌 쪽지를 찾을 수가 없었다. 수학을 포기하는 학생들 대부분은 수학시험에서 이런 느낌을 받기 때문에 포기한다고 생각한다. 수학시험이 누군가에게는 의미없는 보물찾기처럼 느껴지기도 하고 또다른 누군가에게는 침대를 하면서 어몽어스 미션(Task)을 클리어해가듯 부담없고 쉬운 것으로 느껴지는 것이 바로 이 "조건"때문이다. 한 문장 한 문장 곱씹어봐도 모자란데 얼렁뚱땅 넘어간다? 이건 반박을 할 여지 없이 공부를 제대로 하지 않은 사람이다. 공부를 제대로 한 사람은 이 미분가능하다는 조건을 토대로 답에 이른다.
본 글은 이 '미분가능'이라는 조건을 해석하는 "시각"을 제공한다. 이 글을 읽고나면 왜 굳이 「실수 전체에서 미분가능한 함수 f(x)」 라던지, 「f(x)가 실수 전체에서 미분가능할 때」 같은 문장을 문제에(50만명 시험지 뽑으려면 잉크도 아껴야 하는데) 굳이굳이 끼워넣었는지 알 수 있을 것이다. 깨달음을 얻을 수 있다고 자부한다. 어려운 원리를 설명하지는 않는다. 바쁜 수험생들에게 깊은 원리까지 알아갈 시간은 이제 없다. 원론적인 설명보다는 기본개념에서부터 쌓아올리는 설명을 제공하니 겁먹지말도록 :) 가형의 경우와 나형의 경우로 나누어서 글을 쓰니 필요한 부분만 보고 얼른 다시 공부하러 가자
수학 나형에서의 '미분가능'
먼저 어떤 문제에서 미분가능조건이 제시되는지를 보자

2021학년도 9월 수학나형 10번

2021학년도 6월 수학나형 30번

2020학년도 수능 수학나형 20번

2020학년도 6월 수학나형 18번
이런 느낌으로 쉬운 문제부터 30번까지 다양한 번호에 위치하는 '미분가능'조건이다. 이 미분가능이라는 조건은 눈에 보이지는 않지만 사실 한 가지 조건을 내포하고 있다. 바로 연속이다.

분명히 수업시간에 혹은 학원에서 들어본 적이 있을 것이다. "미분가능하면 연속이다" "미분가능하면 연속이야 얘들아" "미분가능하면 연속이죠?" 라고 분명히, 분명히, 당신의 훌륭한 선생님들은 말했을 것이다. 이걸 빼놓고는 위 문제들을 절대로 풀 수가 없기 때문에 만약에 처음듣는 개념이라면 두가지다. 스스로 웹서핑을 통해 선행학습을 진행하고 있는 대한민국의 미래.이거나 제대로 공부하지 않은 학생이거나.
나형에서 미분가능이라는 조건을 제시해주는 형태는 한정되어있다. 어떤 x=a를 기준으로 두 개의 함수를 제시해주고 미분가능하다는 조건을 건다. 실제로 확인된 건 2020학년도 6월부터 2021학년도 9월까지지만 경험상 이것과 다른 형태를 제시해준 적은 없었다. 가형에 비하면 정말 간단한 조건인데, 과외를 하고 질문을 받다보면 많은 학생들이 이 문제를 버린다. 볼 때마다 너무 안타까웠다. 진짜 요플레 떠먹는 수준으로 쉬운데 이걸 버린다. 제발 먹어줘라 ㅠㅠ 뱉지말고..
2021학년도 9월 수학 나형 10번문제를 통해 어떻게 적용하면 좋을 지 알아보자

2021학년도 9월 수학나형 10번
문제해결 과정에 맞추어 차근차근 풀어보면 · · ·
(i) 구해야 하는 것을 정리한다 (이해)
a와 b 두 개의 미지수를 구해야 한다.
(ii) 어떻게 구할 수 있을까? (발상)
미분가능이면 연속이니, 두 개의 식을 도출할 수 있다. 여기서 a와 b를 확정지을 수 있을 것이다.(+연립방정식의 형태로 나오겠군)
(iii) 직접 구해본다 (전개)
(a)식 사용
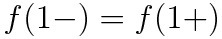
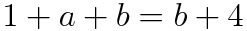
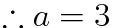
(b)식 사용
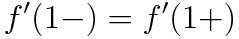
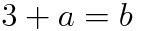
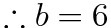
이렇게 미분가능이라는 조건을 해석해주면 된다. "미분가능이면 연속"이라는 말을 꼭 꼭 기억하자! 2020학년도 6월 수학나형 18번 문제도 이와 같은 방식으로 한 번 풀어보자

2020학년도 6월 수학나형 18번
(i) 구해야 하는 것을 정리한다 (이해)
선지 ㄱ,ㄴ,ㄷ의 참,거짓을 판별해야 한다. 그러기 위해서는 g(x)를 이해해야 하는데, g(x)를 이해하기 위해서는 f(x)를 이해해야 한다.
(ii) 어떻게 구할 수 있을까? (발상)
미분가능이면 연속이니, 두 개의 식을 도출할 수 있다. 이를 통해 어느정도 f(x)를 확정지을 수 있을 것 같다. f(x)가 최고차항의 계수가 1인 삼차함수이므로 f(x)를 확정짓기 위해서는 식 세 개가 필요하다. g(x)의 최솟값이 2분의 1보다 작다는 것을 이용해서 f(x)를 유추할 수 있을 것 같다. 일단 f(x)를 미지수 a,b,c를 가지고 가정한 후 미분가능 조건을 이용해보자
(iii) 직접 구해본다 (전개)
a,b,c를 이용해 f(x)를 세우면 다음과 같다.

g(x)가 실수 전체의 집합에서 미분가능하다는 사실은, x=0 즉 g(x)가 달라지는 기점에서도 미분가능하다는 뜻이다. 그래서 우리는 위에서 알아본 (a)식과 (b)식을 이용할 수 있다
(a)식 사용

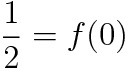
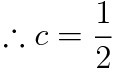
(b)식 사용
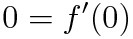
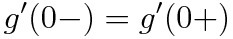
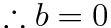
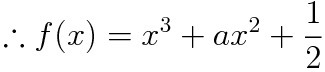
f(x)가 어느정도 틀이 잡혔다. 이제 선지를 하나씩 판별해보자
우리가 f(x)를 구하는 과정에서 ㄱ 선지에 대한 참/거짓 여부를 알게 되었는데,
g(0)=1/2이고 g'(0)=0이므로 ㄱ는 참이다
다음으로 ㄴ 선지의 참/거짓을 판별해보자. g(1) 즉 f(1)이 3/2보다 작냐는 것을 물어본다.
이때
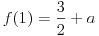
이므로 문제에서는
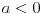
이냐. 라고 물어보고 있는 것이다.
이걸 어떻게 알면 좋을까 하는 건 이제 미분가능조건해석에서 벗어난 이야기이다. 여기까지 "미분가능"이라는 표지판을 보고 잘 따라왔다면 이제는 새로운 표지판을 찾아야 한다. 문제에서 준 조건 중 사용하지 않은 것. 바로 g(x)의 최솟값이 1/2보다 작다는 것. 그것을 사용해보자.
복잡한 계산을 하기 이전에 일단 살펴보자. g(x)는 0보다 작은 구간에서 1/2의 함숫값을 가진다. 그렇다면 최솟값은 어디에 있는가? 0보다 큰 구간 즉 g(x)=f(x)인 구간에서 최솟값을 가진다. 그렇다면 f(x)의 최솟값을 살펴보면 되겠다. f(x)는 삼차함수라고 했는데 최솟값이 존재하려면 극값이 존재해야 하고, 극값이 존재하려면 f'(x)=0이면서 도함수의 부호변화가 있어야 한다.(여기까지 물흐르듯 사고가 전개되는 학생은 정말 훌륭한 학생이다. 계속그렇게 공부하면 된다)
이제 우리가 해야하는 건 f(x)를 미분해서 f'(x)를 살펴보는 것이다.
f(x)를 미분하면 아래와 같다.
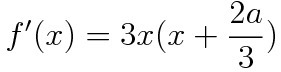
x>0인 x중 f'(x)=0인 x는
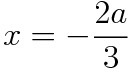
이어야만 한다. 즉 a<0이고(여기서 이미 ㄴ선지는 참이 된다. a<0이냐를 묻고있었으니)
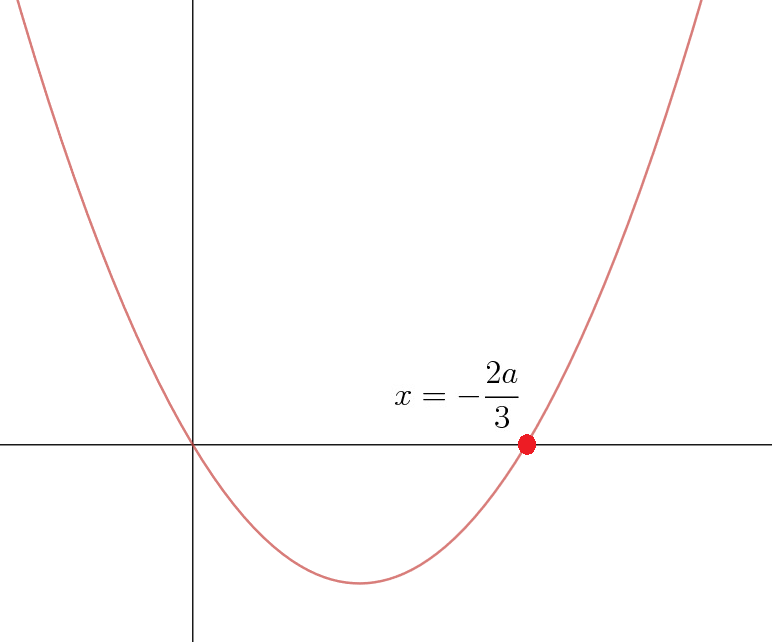
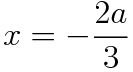
에서 f(x)가 극솟값(최솟값)을 가지므로, g(x)의 최솟값은 f(-2a/3)이 된다. 즉
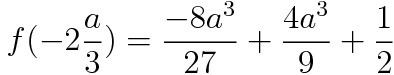
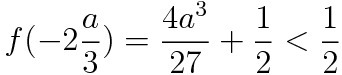
a는 무조건 0보다 작아야 한다.
마지막 ㄷ 선지를 보자. 우리는 위에서 g(x)의 최솟값이 f(-2a/3)임을 알았다. 따라서 최솟값이 0이라는 조건에서 a의 마지막 미지수였던 a의 값을 확정지을 수 있다. 그렇게 되면 자연스럽게 g(2)도 구할 수 있다.
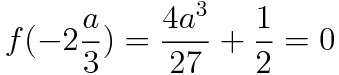
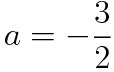
g(2)=f(2)이므로
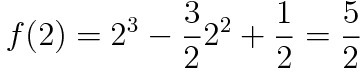
f(2)가 5/2 이다. 따라서 ㄷ 또한 참이다.
풀이에 사용된 부가적인 개념은 둘째치고 미분가능이라는 조건 자체를 알지 못하면 문제에 손을 댈 수 조차 없다는 걸 꼭 알았으면 좋겠다. 거꾸로 미분가능과 같은 사소해보이는 조건 하나에 집중할 때 문제가 수월해진다는 것 또한 기억하길 바란다.
추가로 연속조건의 정의를 올려두니, 한 번 보고 가자

'MATHEMATICS > 고등수학' 카테고리의 다른 글
| [2023학년도 수능] 수학 미적분 29번 손글씨 풀이 (0) | 2022.12.19 |
|---|---|
| 2023학년도 고3 6월 모의고사 기하 29번 손글씨 풀이 (0) | 2022.08.31 |
| 수능에서 '미분가능' 조건의 해석 : 수학 가형 편 (0) | 2022.06.13 |