#유체역학
학부 수준에서는 다루지 않는 심화적인 점성유동 내용이지만 가볍게 읽을 수 있도록 최대한 기초부터 설명하였습니다.
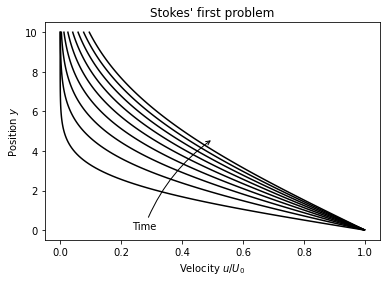
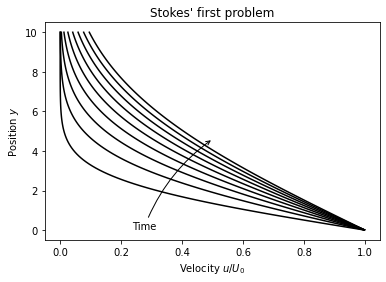
Stokes' first problem은 압력구배가 없는 상황에서, 하단의 flat plat의 움직임에 의해 생기는 유동을 다룹니다.
목차
1. 문제 상황 설명
2. 지배 방정식, IC & BC
3. Solution of stokes' first problem
1. 문제 상황 설명

문제의 상황은 이렇습니다.
정지해있던 무한평판이 갑자기 움직이는 상황(transient; unsteady problem)
① 점성 유동
② 비압축성 유체(ρ = const.)
③ 압력이 일정(p = const. → ▽p = 0)
④ t ≤ 0 까지 평판이 정지해있음
⑤ t 〉0에서 하단의 평판이 속도 U로 움직임
중요한 가정이 두 가지 있는데, u = u(y) 즉 x방향 속도 성분이 오직 y만의 함수라는 것입니다.
사실 무한 평판의 같은 높이에서 모든 x가 같은 속도 성분을 가진다는 것은 자명하므로
거부감 없이 받아들일 수 있습니다.
또 한 가지 중요한 가정은 y방향 속도성분(v)가 0이라는 것입니다.
2. 지배방정식
직교좌표계에서 x방향 나비에 스토크스 방정식은 다음과 같습니다.
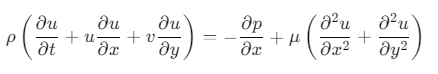
∂u/∂x = 0 이므로 좌변의 둘째, 우변의 둘째 항이 사라집니다.
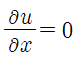
v = 0 이므로 좌변의 셋째 항이 사라지고
압력구배가 0이므로 우변의 첫째 항이 사라집니다.
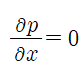
따라서 나비에 스톡스 방정식은 다음과 같이 정리됩니다.
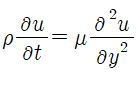
양변을 밀도ρ로 나누면 더 간단히 정리됩니다.
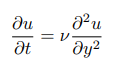
다시 명확히 하자면,
u(y,t)는 x 방향의 유체 속도
ν = μ/ρ 는 동점성계수(kinematic viscosity)
y는 평판으로부터의 거리
t는 시간입니다.
또한 초기조건과 경계조건은 다음과 같습니다.
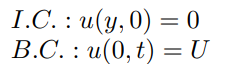
3. Solution of stokes' first problem
일반적으로는 풀 수 없기 때문에, similarity solution을 사용합니다.
similarity solution은 간단히 설명하자면, 속도 프로파일이 어떠한 방향으로 similar하다는 가정 하에 PDE를 ODE로 바꾸어 푸는 방법입니다.
시간에 따른 속도 프로파일이 유사하다고 생각하는거죠
(1) 유사변수(similarity variable) 설정
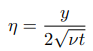
또한 아래와 같이 u = Uf(η)라 가정합니다.

우리의 목적은 저 미지의 함수 f를 구하는 것입니다.
앞서 구한 지배방정식에 넣으면, chain rule에 의해 다음과 같이 정리됩니다.
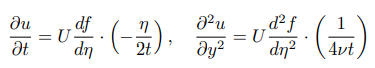

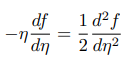
정리하면 최종적으로 아래와 같은 ODE를 얻습니다.
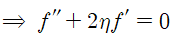
일련의 과정으로 f를 구할 수 있습니다.
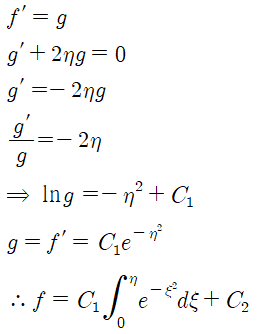
u의 대한 초기조건과 경계조건은 다음과 같이 변환됩니다.
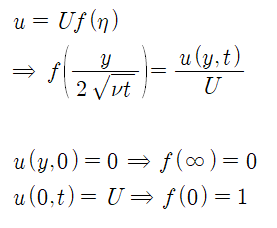
이를 적용하면 다음과 같이 f를 완전히 구할 수 있습니다.
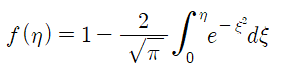
여기서 error function이 등장합니다.
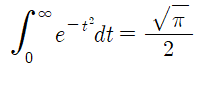
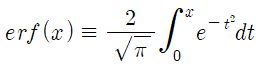
또한 여오차함수(complementary error function)은 다음과 같이 1에서 오차함수(error function)를 뺀 것으로 정의됩니다.

따라서 최종적인 해는 다음과 같습니다.
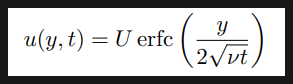
이 속도 분포는 시간에 따라 다음과 같은 분포를 가집니다.