※ 통계분석과 관련된 내용을 다루고 있다
※ 매트랩에서 Statistis and Machine Learning Toolbox 애드온을 설치해야 오늘 다룰 함수들을 사용할 수 있다.
1. anovan
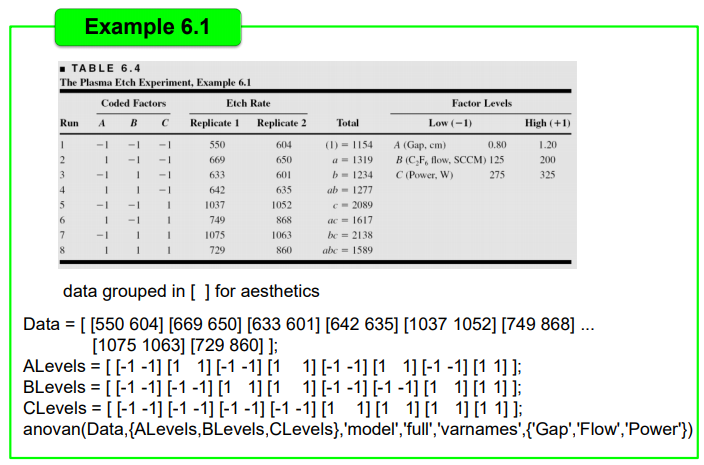
anovan : 다양한 factor들에 대한 분산분석을 시행하는 함수. p-value를 output으로 가지며 F-value, SS 등을 테이블로 보여준다
Data = [ [550 604] [669 650] [633 601] [642 635] [1037 1052] [749 868] ...
[1075 1063] [729 860] ];
ALevels = [[-1 -1] [1 1] [-1 -1] [1 1] [-1 -1] [1 1] [-1 -1] [1 1]];
BLevels = [[-1 -1] [-1 -1] [1 1] [1 1] [-1 -1] [-1 -1] [1 1] [1 1]];
CLevels = [[-1 -1] [-1 -1] [-1 -1] [-1 -1] [1 1] [1 1] [1 1] [1 1]];
p = anovan(Data,{ALevels,BLevels,CLevels},'model','full','varnames',{'Gap','Flow','Power'})factor : A,B,C
각 factor당 level은 두 개씩 존재(A+,A-,B+,B-,C+,C- ; +는 high(또는 있음)를 -는 low(또는 없음)을 의미)
이 예제코드는 시행당 2번의 replicate를 가진다. 이것을 배열 안에 배열로 묶어주었다
Data에는 실험값이, ALevels에는 아래 coded factors 표의 부호가 들어가주면 된다. B,C도 마찬가지
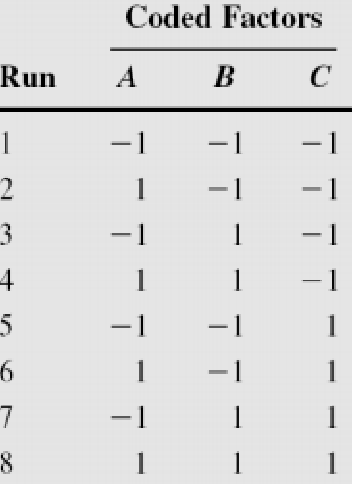
각 시행은 1,A,B,AB,C,AC,BC,ABC 를 의미하는데 factor가 두 개 이상 있는 것은 interaction 항이다.
코드를 실행하면 다음과 같은 분산분석표가 나온다
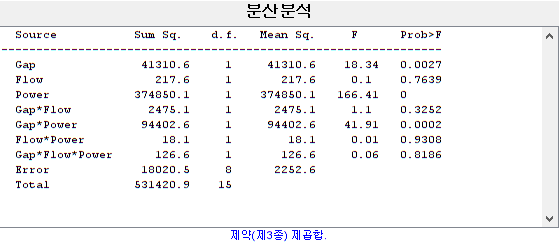
> 분산분석 표로부터 다음과 같은 해석을 가져간다
F value가 높으면 significant factor
p value가 작으면 significant factor
즉 significant factor는 Gap, Power, Gap*power(interaction) 세 가지이다
2. fitlm
선형 회귀 모델을 만드는 함수
tbl = table(ALevels',BLevels',CLevels',Data', 'VariableNames',{'A','B','C','Etch_Rate'})
mdl1 = fitlm(tbl,'Etch_Rate~A*B*C','ResponseVar','Etch_Rate','PredictorVars',{'A','B','C'})
mdl2 = fitlm(tbl,'Etch_Rate~A*C','ResponseVar','Etch_Rate','PredictorVars',{'A','C'})
먼저 table 함수를 사용해 table형 배열을 선언한다.
위 코드에서 조금 잘못 보이는 것이 있는데 table함수 내 열벡터를 넣어주기 위해 transpose(')를 해준 것이지 문자열을 입력한 것이 아니다
table(codedfactors . . . , 'VariableNames', {변수 이름들}) 형식으로 입력해준다.
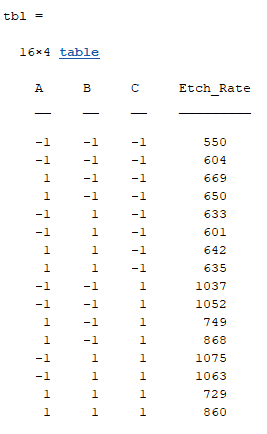
(A,B,C) 부호가 두 번씩 반복되는 것은 앞서 anovan에서 살펴봤듯이 replicate = 2 인 실험데이터이기 때문
다음으로 fitlm 함수를 사용한다.
fitlm함수의 lm은 linear model의 약자로 이 함수는 선형 회귀 모델은 만들어준다
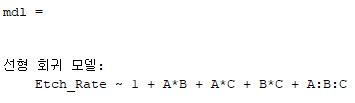
fitlm(tbl,'output이름~factor들(Wilkinson notation사용가능)','ResponseVar','output이름','PredcitorVars',{factor1, factor2, . . . }) 형식으로 입력
'ResponseVar', 'PredcitorVars' 는 고정
wilkinson notation이란 matlab 통계분석에서 많은 factor들에 대해 모두 입력하기가 번거로우니 간단히 나타낸 표기법이다

제외하는 factor가 없으니 A*B*C라 입력해주면 1,A,B,C,AB,AC,BC,ABC 8가지 항으로 구성된 회귀분석이 수행된다
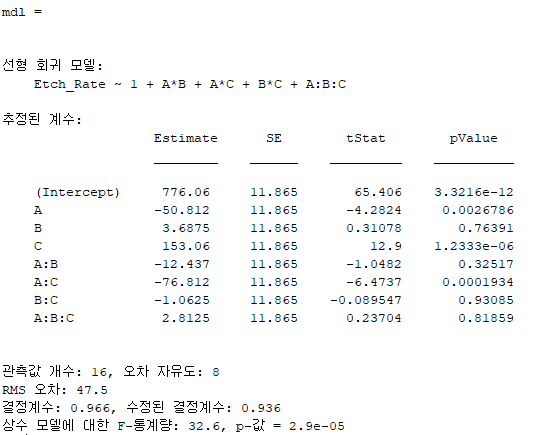
1 + A*B + A*C + B*C + A:B:C 다섯 개의 항이 아니라
wilkinson notation으로 표시된 것이기 때문에 1+A+B+C+AB+AC+BC+ABC 를 의미한다
세 번째 줄의 코드는 앞서 anovan으로 구한 significant factor들로 구성한 선형 회귀 모델이다
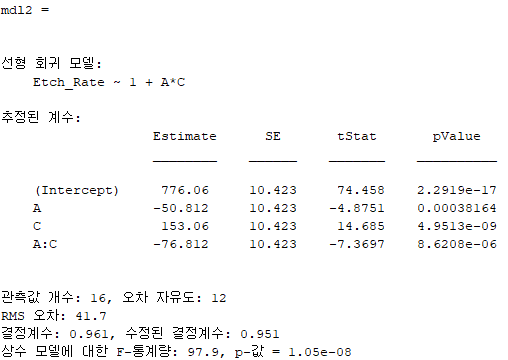
3. response surface
X1 = -1:0.1:1
X2 = X1
[A,C]=meshgrid(X1,X2)
etch_rate=776.06-50.813*A+153.06*C-76.812*A.*C
Gap = linspace(0.8,1.2,21)
Power = linspace(275,325,21)
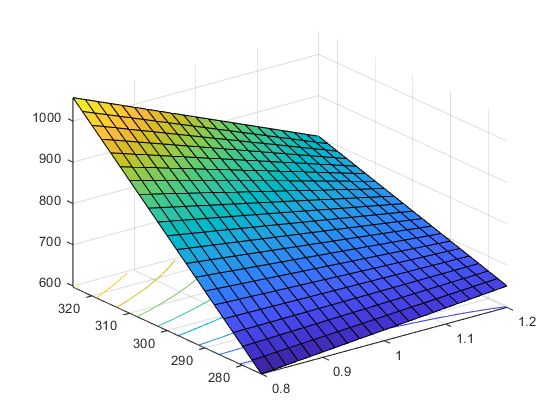
surfc(Gap,Power,etch_rate)
x1은 -1부터 1까지 0.1 간격인 배열인데, 이것을 생성해서 meshgrid를 만드는 이유는
각 factor가 -1(low)부터 +1(high)까지인 격자를만들기 위해서다
linspace는 구간의 시작과 끝에 대해 등간격으로 배열을 만들어주는데 앞선 예제의 low, high factor level에 맞춰 만들어준다
x1, x2의 크기가 21이기 때문에 마지막에 21이 들어갔다

'개발 > 매트랩' 카테고리의 다른 글
| [매트랩] 논리 인덱싱(logical indexing) (0) | 2023.12.29 |
|---|---|
| [매트랩] diag 함수로 주대각 원소 추출하기, 대각행렬 생성하기 (0) | 2022.12.30 |
| [매트랩] meshgrid 로 모든 원소의 곱셈 수행하기 (0) | 2022.12.28 |
| [매트랩] 콜론 연산자(:)와 end 이용해서 행렬에서 특정 행, 열 뽑아내기 (0) | 2022.12.27 |
| [매트랩] 행렬을 열벡터로 변환, 난수 생성 (0) | 2022.12.26 |